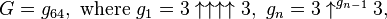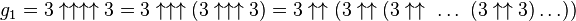Graham's number

From Wikipedia, the free encyclopedia

Graham's number, named after Ronald Graham, is a large number that is an upper bound on the solution to a certain problem in Ramsey theory. This number gained a degree of popular attention when Martin Gardner described it in the "Mathematical Games" section of Scientific American in November 1977, writing that "In an unpublished proof, Graham has recently established ... a bound so vast that it holds the record for the largest number ever used in a serious mathematical proof." The 1980 Guiness Book of World Records repeated Gardner's claim, adding to the popular interest in this number. Graham's number is much larger than other well-known large numbers such as a googol, googolplex, and a googol multiplex, and even larger than Skewes' number and Moser's number. Indeed, it is not possible, given the limitations of our universe, to denote Graham's number, or any reasonable approximation of it, in a conventional system of numeration. Even "power towers" of the form $a ^{ b ^{ c ^{ \cdot ^{ \cdot ^{ \cdot}}}}}$ are useless for this purpose, although it can be easily described by recursive formulas using Knuth's up-arrow notation or the equivalent, as was done by Graham. The last ten digits of Graham's number are ...2464195387.

Specific integers known to be far larger than Graham's number have since appeared in many serious mathematical proofs (e.g., in connection with Friedman's various finite forms of Kruskal's theorem).

[edit] Graham's problem

Graham's number is connected to the following problem in the branch of mathematics known as Ramsey theory:

Consider an n-dimensional hypercube, and connect each pair of vertices to obtain a complete graph on $2 n$ vertices. Then colour each of the edges of this graph using only the colours red and black. What is the smallest value of n for which every possible such colouring must necessarily contain a single-coloured complete sub-graph with 4 vertices which lie in a plane?

Graham & Rothschild [1971] proved that this problem has a solution, N*, and gave as a bounding estimate 6 ≤ N* ≤ N, with N a particular, explicitly defined, very large number; however, Graham (in unpublished work) revised this upper bound to be a much larger number. Graham's revised upper bound was later published — and dubbed "Graham's number" — by Martin Gardner in [Scientific American, "Mathematical Games", November 1977].

The lower bound was later improved by Exoo[2003], who showed the solution to be at least 11, and provided experimental evidence suggesting that it is at least 12. Thus, the best known bounding estimate for the solution N* is 11 ≤ N* ≤ G, where G is Graham's number.

[edit] Definition of Graham's number

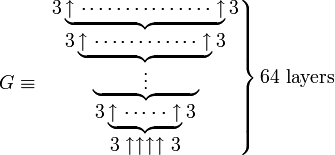
Using Knuth's up-arrow notation, Graham's number G (as defined in Gardner's Scientific American article) is

$\left. \begin{matrix} &3\underbrace{\uparrow \cdots\cdots\cdots\cdots\cdots \uparrow}3 \\ &3\underbrace{\uparrow \cdots\cdots\cdots\cdots \uparrow}3 \\ G \equiv &\underbrace{\qquad\;\; \vdots \qquad\;\;} \\ &3\underbrace{\uparrow \cdots\cdot\cdot \uparrow}3 \\ &3\uparrow \uparrow \uparrow \uparrow3 \end{matrix} \right \} \text{64 layers}$

where the number of arrows in each layer, starting at the top layer, is specified by the value of the next layer below it; that is,

$G = g_{64},\text{ where }g_1=3\uparrow\uparrow\uparrow\uparrow 3,\ g_n = 3\uparrow^{g_{n-1}}3,$

where a superscript on an up-arrow indicates how many arrows there are. In other words, G is calculated in 64 steps: the first step is to calculate g₁ with four up-arrows between 3s; the second step is to calculate g₂ with g₁ up-arrows between 3s, the third step is to calculate g₃ with g₂ up-arrows between 3s, and so on, until finally calculating G = g₆₄ with g₆₃ up-arrows between 3s.

Equivalently,

$G = f^{64}(4),\text{ where }f(n) = 3 \uparrow^n 3,$

where a superscript on f indicates iteration of the function. The function f is a special case of the hyper() family of functions, $f (n) = hyper(3, n + 2,3)$ , and can also be expressed in Conway chained arrow notation as $f(n) = 3 \rightarrow 3 \rightarrow n$ . The latter notation also provides the following bounds on G:

$3\rightarrow 3\rightarrow 64\rightarrow 2 < G < 3\rightarrow 3\rightarrow 65\rightarrow 2.\,$

[edit] Magnitude of Graham's number

To convey the difficulty of appreciating the enormous size of Graham's number, it may be helpful to express — in terms of exponentiation alone — just the first term (g₁) of the rapidly growing 64-term sequence. First, in terms of tetration ( $\uparrow\uparrow$ ) alone:

$g_1 = 3 \uparrow \uparrow \uparrow \uparrow 3 = 3 \uparrow \uparrow \uparrow (3 \uparrow \uparrow \uparrow 3) = 3 \uparrow\uparrow (3 \uparrow\uparrow (3 \uparrow\uparrow \ \dots \ (3 \uparrow\uparrow 3) \dots ))$

where the number of 3s in the expression on the right is

$3 \uparrow \uparrow \uparrow 3 \ = \ 3 \uparrow \uparrow (3 \uparrow \uparrow 3).$

Now each tetration ( $\uparrow\uparrow$ ) operation reduces to a "tower" of exponentiations ( $\uparrow$ ) according to the definition

$3 \uparrow\uparrow X \ = \ 3 \uparrow (3 \uparrow (3 \uparrow \dots (3 \uparrow 3) \dots )) \ = \ 3^{3^{\cdot^{\cdot^{\cdot^{3}}}}} \quad \text{where there are X 3s}.$

Thus,

$g_1 = 3 \uparrow\uparrow (3 \uparrow\uparrow (3 \uparrow\uparrow \ \dots \ (3 \uparrow\uparrow 3) \dots )) \quad \text{where the number of 3s is} \quad 3 \uparrow \uparrow (3 \uparrow \uparrow 3)$

becomes, solely in terms of repeated "exponentiation towers",

$g_1 = \left. \begin{matrix}3^{3^{\cdot^{\cdot^{\cdot^{\cdot^{3}}}}}}\end{matrix} \right \} \left. \begin{matrix}3^{3^{\cdot^{\cdot^{\cdot^{3}}}}}\end{matrix} \right \} \dots \left. \begin{matrix}3^{3^3}\end{matrix} \right \} 3 \quad \text{where the number of towers is} \quad \left. \begin{matrix}3^{3^{\cdot^{\cdot^{\cdot^{3}}}}}\end{matrix} \right \} \left. \begin{matrix}3^{3^3}\end{matrix} \right \} 3$

and where the number of 3s in each tower, starting from the leftmost tower, is specified by the value of the next tower to the right.

The magnitude of this first term, g₁, is so large that it is practically incomprehensible, even though the above display is relatively easy to comprehend. (Even the mere number of towers in this formula for g₁ is far greater than the number of Planck volumes into which one can imagine subdividing the observable universe.) And after this first term, there still remain another 63 terms in the rapidly growing g sequence before Graham's number G = g₆₄ is reached.

[edit] Rightmost decimal digits of Graham's number

Graham's number is a "power tower" of the form 3 $\uparrow\uparrow$ n (with a very large value of n), so its least-significant decimal digits must satisfy certain properties common to all such towers. One of these properties is that all such towers of height greater than d (say), have the same sequence of d rightmost decimal digits. This is a special case of a more general property: The d rightmost decimal digits of all such towers of height greater than d+2, are independent of the topmost "3" in the tower; i.e., the topmost "3" can be changed to any other nonnegative integer without affecting the d rightmost digits.

The following table illustrates, for a few values of d, how this happens. For a given height of tower and number of digits d, the full range of d-digit numbers (10^d of them) does not occur; instead, a certain smaller subset of values repeats itself in a cycle. The length of the cycle and some of the values (in parentheses) are shown in each cell of this table:

Number of different possible values of 3 $\uparrow$ 3 $\uparrow$ ...3 $\uparrow$ x when all but the rightmost d decimal digits are ignored
Number of digits (d)	3 $\uparrow$ x	3 $\uparrow$ 3 $\uparrow$ x	3 $\uparrow$ 3 $\uparrow$ 3 $\uparrow$ x	3 $\uparrow$ 3 $\uparrow$ 3 $\uparrow$ 3 $\uparrow$ x	3 $\uparrow$ 3 $\uparrow$ 3 $\uparrow$ 3 $\uparrow$ 3 $\uparrow$ x
1	4 (1,3,9,7)	2 (3,7)	1 (7)	1 (7)	1 (7)
2	20 (01,03,...,87,...,67)	4 (03,27,83,87)	2 (27,87)	1 (87)	1 (87)
3	100 (001,003,...,387,...,667)	20 (003,027,...387,...,587)	4 (027,987,227,387)	2 (987,387)	1 (387)

The particular rightmost d digits that are ultimately shared by all sufficiently tall towers of 3s are in bold text, and can be seen developing as the tower height increases. For any fixed number of digits d (row in the table), the number of values possible for 3 $\uparrow$ 3 $\uparrow$ ...3 $\uparrow$ x mod 10^d, as x ranges over all nonnegative integers, is seen to decrease steadily as the height increases, until eventually reducing the "possibility set" to a single number (colored cells) when the height exceeds d+2.

A simple algorithm ^[1] for computing these digits may be described as follows: let x = 3, then iterate, d times, the assignment x = 3^x mod 10^d. The final value assigned to x (as a base-ten numeral) is then composed of the d least-significant decimal digits of 3 $\uparrow\uparrow$ n, for all n > d. (If the final value of x has only d-1 decimal digits, add a leading 0.)

This algorithm produces the following 100 rightmost decimal digits of Graham's number (or any tower of more than 100 3s):

...9404248265018193851562535
   7963996189939679054966380
   0322234872396701848518643
   9059104575627262464195387.

[edit] See also

TREE(3)

[edit] Notes

^ The Math Forum @ Drexel ("Last Eight Digits of Z")

[edit] References

Graham, R. L.; Rothschild, B. L. (1971). "Ramsey's Theorem for n-Parameter Sets". Transactions of the American Mathematical Society 159: 257–292. doi:10.2307/1996010.
Gardner, Martin (November 1977). "Mathematical Games". Scientific American 237: 18–28. ; reprinted (revised 2001) in the following book:
Gardner, Martin (2001). The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems. New York, NY: Norton. ISBN 0393020231.
Gardner, Martin (1989). Penrose Tiles to Trapdoor Ciphers. Washington, D.C.: Mathematical Association of America. ISBN 0-88385-521-6.
Exoo, Geoffrey (2003). "A Euclidean Ramsey Problem". Discrete Computational Geometry 29: 223–227. doi:10.1007/s00454-002-0780-5.

[edit] External links

[0] The Math Forum @ Drexel ("Last Eight Digits of Z")

[1]

Graham's number

From Wikipedia, the free encyclopedia

Contents

[edit] Graham's problem

[edit] Definition of Graham's number

[edit] Magnitude of Graham's number

[edit] Rightmost decimal digits of Graham's number

[edit] See also

[edit] Notes

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages