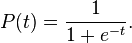Sigmoid function
From Wikipedia, the free encyclopedia
| This article needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (May 2008) |

Many natural processes and complex system learning curves display a history dependent progression from small beginnings that accelerates and approaches a climax over time. For lack of complex descriptions a sigmoid function is often used. A sigmoid curve is produced by a mathematical function having an "S" shape. Often, sigmoid function refers to the special case of the logistic function shown at right and defined by the formula
Another example is the Gompertz curve. It is used in modeling systems that saturate at large values of t.
Contents |
[edit] Properties
In general, a sigmoid function is real-valued and differentiable, having either a non-negative or non-positive first derivative and exactly one inflection point. There are also two asymptotes,  .
.
The general case 1 / (1 + e-x) is particularly useful, used in Artificial Neural Networks partly because it has a simple derivative: if s(x) is the sigmoid function, then s'(x) = s(x) * (1 - s(x)).[1]
[edit] Examples
Besides the logistic function, sigmoid functions include the ordinary arc-tangent, the hyperbolic tangent, and the error function, but also the Gompertz function, the generalised logistic function, and algebraic functions like  .
.
The integral of any smooth, positive, "bump-shaped" function will be sigmoidal, thus the cumulative distribution functions for many common probability distributions are sigmoidal.
[edit] See also
[edit] References
- Tom M. Mitchell, Machine Learning, WCB-McGraw-Hill, 1997, ISBN 0-07-042807-7. In particular see "Chapter 4: Artificial Neural Networks" (in particular p. 96-97) where Mitchel uses the word "logistic function" and the "sigmoid function" synonymously -- this function he also calls the "squashing function" -- and the sigmoid (aka logistic) function is used to compress the outputs of the "neurons" in multi-layer neural nets.