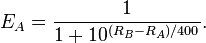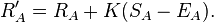Elo rating system
From Wikipedia, the free encyclopedia
| This article may need to be rewritten entirely to comply with Wikipedia's quality standards, as it is written in an unencyclopedic style (especially towards the end).. You can help. The discussion page may contain suggestions. (February 2009) |
The Elo rating system is a method for calculating the relative skill levels of players in two-player games such as chess and Go. It is named after its creator Arpad Elo (1903–1992, born as Élő Árpád), a Hungarian-born American physics professor.
The Elo system was invented as an improved chess rating system, but today it is also used in many other games. It is also used as a rating system for multiplayer competition in a number of computer games, and has been adapted to team sports including association football, American college football and basketball, and Major League Baseball.
Contents |
[edit] History
| This section does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (March 2007) |
Arpad Elo was a master-level chess player and an active participant in the United States Chess Federation (USCF) from its founding in 1939.[1] The USCF used a numerical ratings system, devised by Kenneth Harkness, to allow members to track their individual progress in terms other than tournament wins and losses. The Harkness system was reasonably fair, but in some circumstances gave rise to ratings which many observers considered inaccurate. On behalf of the USCF, Elo devised a new system with a more statistical basis.
Elo's system replaced earlier systems of competitive rewards with a system based on statistical estimation. Rating systems for many sports award points in accordance with subjective evaluations of the 'greatness' of certain achievements. For example, winning an important golf tournament might be worth an arbitrarily chosen five times as many points as winning a lesser tournament.
A statistical endeavor, by contrast, uses a model that relates the game results to underlying variables representing the ability of each player.
Elo's central assumption was that the chess performance of each player in each game is a normally distributed random variable. Although a player might perform significantly better or worse from one game to the next, Elo assumed that the mean value of the performances of any given player changes only slowly over time. Elo thought of a player's true skill as the mean of that player's performance random variable.
A further assumption is necessary, because chess performance in the above sense is still not measurable. One cannot look at a sequence of moves and say, "That performance is 2039." Performance can only be inferred from wins, draws and losses. Therefore, if a player wins a game, he is assumed to have performed at a higher level than his opponent for that game. Conversely if he loses, he is assumed to have performed at a lower level. If the game is a draw, the two players are assumed to have performed at nearly the same level.
Elo did not specify exactly how close two performances ought to be to result in a draw as opposed to a win or loss. And while he thought it likely that each player might have a different standard deviation to his performance, he made a simplifying assumption to the contrary.
To simplify computation even further, Elo proposed a straightforward method of estimating the variables in his model (i.e., the true skill of each player). One could calculate relatively easily, from tables, how many games a player is expected to win based on a comparison of his rating to the ratings of his opponents. If a player won more games than he was expected to win, his rating would be adjusted upward, while if he won fewer games than expected his rating would be adjusted downward. Moreover, that adjustment was to be in exact linear proportion to the number of wins by which the player had exceeded or fallen short of his expected number of wins.
From a modern perspective, Elo's simplifying assumptions are not necessary because computing power is inexpensive and widely available. Moreover, even within the simplified model, more efficient estimation techniques are well known. Several people, most notably Mark Glickman, have proposed using more sophisticated statistical machinery to estimate the same variables. On the other hand, the computational simplicity of the Elo system has proven to be one of its greatest assets. With the aid of a pocket calculator, an informed chess competitor can calculate to within one point what his next officially published rating will be, which helps promote a perception that the ratings are fair.
[edit] Implementing Elo's scheme
The USCF implemented Elo's suggestions in 1960,[2] and the system quickly gained recognition as being both fairer and more accurate than the Harkness system. Elo's system was adopted by FIDE in 1970. Elo described his work in some detail in the book The Rating of Chessplayers, Past and Present, published in 1978.
Subsequent statistical tests have shown that chess performance is almost certainly not normally distributed. Weaker players have significantly greater winning chances than Elo's model predicts. Therefore, both the USCF and FIDE have switched to formulas based on the logistic distribution. However, in deference to Elo's contribution, both organizations are still commonly said to use "the Elo system".
[edit] Different ratings systems
The phrase "Elo rating" is often used to mean a player's chess rating as calculated by FIDE. However, this usage is confusing and often misleading, because Elo's general ideas have been adopted by many different organizations, including the USCF (before FIDE), the Internet Chess Club (ICC), Yahoo! Games, and the now defunct Professional Chess Association (PCA). Each organization has a unique implementation, and none of them precisely follows Elo's original suggestions. It would be more accurate to refer to all of the above ratings as Elo ratings, and none of them as the Elo rating.
Instead one may refer to the organization granting the rating, e.g. "As of August 2002, Gregory Kaidanov had a FIDE rating of 2638 and a USCF rating of 2742." It should be noted that the Elo ratings of these various organizations are not always directly comparable. For example, someone with a FIDE rating of 2500 will generally have a USCF rating near 2600 and an ICC rating in the range of 2500 to 3100.
[edit] FIDE ratings
For top players, the most important rating is their FIDE rating. FIDE issues a ratings list four times a year.
The following analysis of the January 2006 FIDE rating list gives a rough impression of what a given FIDE rating means:
- 17171 players have a rating between 2200 and 2399, and are usually associated with the Candidate Master title.
- 1868 players have a rating between 2400 and 2499, most of whom have either the IM or the GM title.
- 563 players have a rating between 2500 and 2599, most of whom have the GM title
- 123 players have a rating between 2600 and 2699, all (but one) of whom have the GM title
- 18 players have a rating between 2700 and 2799
- Only 4 players (Garry Kasparov, Vladimir Kramnik, Veselin Topalov and Viswanathan Anand) have ever exceeded a rating of 2800, and only Topalov does in the latest (April 2009) list.
The highest ever FIDE rating was 2851, which Garry Kasparov had on the July 1999 and January 2000 lists.
In the whole history of FIDE rating system, only 48 players (to October 2007), sometimes called "Super-grandmasters", have achieved a peak rating of 2700 or more.
[edit] Performance rating
Performance Rating is a hypothetical rating that would result from the games of a single event only. Some chess organizations use the "algorithm of 400" to calculate performance rating. According to this algorithm, performance rating for an event is calculated by taking (1) the rating of each player beaten and adding 400, (2) the rating of each player lost to and subtracting 400, (3) the rating of each player drawn, and (4) summing these figures and dividing by the number of games played.
FIDE, however, calculates performance rating by means of the formula: Opponents' Rating Average + Rating Difference. Rating Difference dp is based on a player's tournament percentage score p, which is then used as the key in a lookup table. p is simply the number of points scored divided by the number of games played. Note that, in case of a perfect or no score dp is indeterminate. The full table can be found in the FIDE handbook online. A simplified version of this table looks like this:
| p | dp |
|---|---|
| 0.99 | +677 |
| 0.9 | +366 |
| 0.8 | +240 |
| 0.7 | +149 |
| 0.6 | +72 |
| 0.5 | 0 |
| 0.4 | -72 |
| 0.3 | -149 |
| 0.2 | -240 |
| 0.1 | -366 |
| 0.01 | -677 |
[edit] FIDE tournament categories
FIDE classifies tournaments into categories according to the average rating of the players. Each category is 25 rating points wide. Category 1 is for an average rating of 2251 to 2275, category 2 is 2276 to 2300, etc.[3] The highest rated tournaments have been Category 21, with an average from 2751 to 2775. The top categories are as follows:
| Category | Average rating |
|---|---|
| 10 | 2476 to 2500 |
| 11 | 2501 to 2525 |
| 12 | 2526 to 2550 |
| 13 | 2551 to 2575 |
| 14 | 2576 to 2600 |
| 15 | 2601 to 2625 |
| 16 | 2626 to 2650 |
| 17 | 2651 to 2675 |
| 18 | 2676 to 2700 |
| 19 | 2701 to 2725 |
| 20 | 2726 to 2750 |
| 21 | 2751 to 2775 |
[edit] Live ratings
FIDE updates its ratings list every three months. In contrast, the unofficial "Live ratings" calculate the change in players' ratings after every game. These Live ratings are based on the previously published FIDE ratings, so a player's Live rating is intended to correspond to what the FIDE rating would be if FIDE was to issue a new list that day.
Although Live ratings are unofficial, interest arose in Live ratings in August/September 2008 when five different players took the "Live" #1 ranking.[4]
The unofficial live ratings are published and maintained by Hans Arild Runde at http://chess.liverating.org . Only players over 2700 are covered.
[edit] United States Chess Federation ratings
The United States Chess Federation (USCF) uses its own classification of players: [5]
- 2400 and above: Senior Master
- 2200–2399: Master
- 2000–2199: Expert
- 1800–1999: Class A
- 1600–1799: Class B
- 1400–1599: Class C
- 1200–1399: Class D
- 1000–1199: Class E
In general, 1000 is considered a bright beginner. The average tournament player's rating in the USCF from 1400-1500. Class B and higher is generally considered extremely competitive and the USCF establishes a rating floor. A floor is your current rating minus 200 rating points. For instance, once someone has reached a rating of 1600, they can never fall below 1400 for rating and competition purposes. (To protect the integrity of big tournaments and combat sandbagging).
The K factor, in the USCF rating system, can be estimated by dividing 800 by the effective number of games a player's rating is based on (Ne) plus the number of games the player completed in a tournament (m).[6]
[edit] Ratings of computers
Since 2005–2006, human-computer chess matches have demonstrated that chess computers are stronger than the strongest human players. However ratings of computers are difficult to quantify. There have been too few games under tournament conditions to give computers or software engines an accurate rating.[7] Also, for chess engines, the rating is dependent on the machine a program runs on.
For some ratings estimates, see Chess Engines rating lists.
[edit] Theory
[edit] Mathematical details
Performance can't be measured absolutely; it can only be inferred from wins and losses. Ratings therefore have meaning only relative to other ratings. Therefore, both the average and the spread of ratings can be arbitrarily chosen. Elo suggested scaling ratings so that a difference of 200 rating points in chess would mean that the stronger player has an expected score of approximately 0.75, and the USCF initially aimed for an average club player to have a rating of 1500.
A player's expected score is his probability of winning plus half his probability of drawing. Thus an expected score of 0.75 could represent a 75% chance of winning, 25% chance of losing, and 0% chance of drawing. On the other extreme it could represent a 50% chance of winning, 0% chance of losing, and 50% chance of drawing. The probability of drawing, as opposed to having a decisive result, is not specified in the Elo system. Instead a draw is considered half a win and half a loss.
If Player A has true strength RA and Player B has true strength RB, the exact formula (using the logistic curve) for the expected score of Player A is
Similarly the expected score for Player B is
This could also be expressed by
and
where  and
and 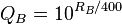 . Note that the same denominator applies to both expressions. This means that by studying only the numerators, we find out that player A has about QA / QB times greater chance of winning as player B. It then follows that for each 400 rating points of advantage over the opponent, the chance of winning is magnified ten times in comparison to the opponent's chance of winning.
. Note that the same denominator applies to both expressions. This means that by studying only the numerators, we find out that player A has about QA / QB times greater chance of winning as player B. It then follows that for each 400 rating points of advantage over the opponent, the chance of winning is magnified ten times in comparison to the opponent's chance of winning.
Also note that EA + EB = 1. In practice, since the true strength of each player is unknown, the expected scores are calculated using the player's current ratings.
When a player's actual tournament scores exceed his expected scores, the Elo system takes this as evidence that player's rating is too low, and needs to be adjusted upward. Similarly when a player's actual tournament scores fall short of his expected scores, that player's rating is adjusted downward. Elo's original suggestion, which is still widely used, was a simple linear adjustment proportional to the amount by which a player overperformed or underperformed his expected score. The maximum possible adjustment per game (sometimes called the K-value) was set at K = 16 for masters and K = 32 for weaker players.
Supposing Player A was expected to score EA points but actually scored SA points. The formula for updating his rating is
This update can be performed after each game or each tournament, or after any suitable rating period. An example may help clarify. Suppose Player A has a rating of 1613, and plays in a five-round tournament. He loses to a player rated 1609, draws with a player rated 1477, defeats a player rated 1388, defeats a player rated 1586, and loses to a player rated 1720. His actual score is (0 + 0.5 + 1 + 1 + 0) = 2.5. His expected score, calculated according to the formula above, was (0.506 + 0.686 + 0.785 + 0.539 + 0.351) = 2.867. Therefore his new rating is (1613 + 32· (2.5 − 2.867)) = 1601.
Note that while two wins, two losses, and one draw may seem like a par score, it is worse than expected for Player A because his opponents were lower rated on average. Therefore he is slightly penalized. If he had scored two wins, one loss, and two draws, for a total score of three points, that would have been slightly better than expected, and his new rating would have been (1613 + 32· (3 − 2.867)) = 1617.
This updating procedure is at the core of the ratings used by FIDE, USCF, Yahoo! Games, the ICC, and FICS. However, each organization has taken a different route to deal with the uncertainty inherent in the ratings, particularly the ratings of newcomers, and to deal with the problem of ratings inflation/deflation. New players are assigned provisional ratings, which are adjusted more drastically than established ratings, and various methods (none completely successful) have been devised to inject points into the rating system so that ratings from different eras are roughly comparable.
The principles used in these rating systems can be used for rating other competitions—for instance, international football matches.
Elo ratings have also been applied to games without the possibility of draws, and to games in which the result can also have a quantity (small/big margin) in addition to the quality (win/loss). See go rating with Elo for more.
See also: Hubbert curve for the similarity between the derivative of the logistic curve and the normal distribution.
[edit] Mathematical issues
There are three main mathematical concerns relating to the original work of Professor Elo, namely the correct curve, the correct K-factor, and the provisional period crude calculations.
[edit] Most accurate distribution model
The first major mathematical concern addressed by both FIDE and the USCF was the use of the normal distribution. They found that this did not accurately represent the actual results achieved by particularly the lower rated players. Instead they switched to a logistical distribution model, which provides a better fit for the actual results achieved.[8]
[edit] Most accurate K-factor
The second major concern is the correct "K-factor" used. The chess statistician Jeff Sonas reckons that the original K=10 value (for players rated above 2400) is inaccurate in Elo's work. If the K-factor coefficient is set too large, there will be too much sensitivity to winning, losing or drawing, in terms of the large number of points exchanged. Too low a K-value, and the sensitivity will be minimal, and it would be hard to achieve a significant number of points for winning, etc.
Elo's original K-factor estimation was made without the benefit of huge databases and statistical evidence. Sonas indicates that a K-factor of 24 (for players rated above 2400) may be more accurate both as a predictive tool of future performance, and also more sensitive to performance.[9]
Certain Internet chess sites seem to avoid a three-level K-factor staggering based on rating range. For example the ICC seems to adopt a global K=32 except when playing against provisionally rated players. The USCF (which makes use of a logistic distribution as opposed to a normal distribution) have staggered the K-factor according to three main rating ranges of:
- Players below 2100 -> K factor of 32 used
- Players between 2100 and 2400 -> K factor of 24 used
- Players above 2400 -> K factor of 16 used
FIDE uses the following ranges[10]:
- K = 25 for a player new to the rating list until he has completed events with a total of at least 30 games.
- K = 15 as long as a player's rating remains under 2400.
- K = 10 once a player's published rating has reached 2400, and he has also completed events with a total of at least 30 games. Thereafter it remains permanently at 10.
In over-the-board chess, the staggering of K-factor is important to ensure minimal inflation at the top end of the rating spectrum. This assumption might in theory apply equally to an online chess server, as well as a standard over-the-board chess organisation such as FIDE or USCF. In theory, it would make it harder for players to get the much higher ratings, if their K-factor sensitivity was lessened from 32 to 16 for example, when they get over 2400 rating. However, the ICC's help on K-factors indicates[11] that it may simply be the choosing of opponents that enables 2800+ players to further increase their rating quite easily. This would seem to hold true, for example, if one analysed the games of a GM on the ICC: one can find a string of games of opponents who are all over 3100. In over-the-board chess, it would only be in very high level all-play-all events that this player would be able to find a steady stream of 2700+ opponents – in at least a category 15+ FIDE event. A category 10 FIDE event would mean players are restricted in rating between 2476 to 2500. However, if the player entered normal Swiss-paired open over-the-board chess tournaments, he would likely meet many opponents less than 2500 FIDE on a regular basis. A single loss or draw against a player rated less than 2500 would knock the GM's FIDE rating down significantly.
Even if the K-factor was 16, and the player defeated a 3100+ player several games in a row, his rating would still rise quite significantly in a short period of time, due to the speed of blitz games, and hence the ability to play many games within a few days. The K-factor would arguably only slow down the increases that the player achieves after each win. The evidence given in the ICC K-factor article relates to the auto-pairing system, where the maximum ratings achieved are seen to be only about 2500. So it seems that random-pairing as opposed to selective pairing is the key for combatting rating inflation at the top end of the rating spectrum, and possibly only to a much lesser extent, a slightly lower K-factor for a player >2400 rating.
[edit] Practical issues
[edit] Game activity versus protecting one's rating
|
This section has multiple issues. Please help improve the article or discuss these issues on the talk page.
|
In general the Elo system has increased the competitive climate for chess and inspired players for further study and improvement of their game.[citation needed] However, in some cases ratings can discourage game activity for players who wish to "protect their rating".
Examples:
- They may choose their events or opponents more carefully where possible.
- If a player is in a Swiss tournament, and loses a couple of games in a row, they may feel the need to abandon the tournament in order to avoid any further rating "damage".
- Junior players, who may have high provisional ratings, and who should really be practicing as much as possible,[citation needed] might play less than they would, because of rating concerns.
In these examples, the rating "agenda" can sometimes conflict with the agenda of promoting chess activity and rated games. [12]
Some of the clash of agendas between game activity, and rating concerns is also seen on many servers online which have implemented the Elo system. For example, the higher rated players, being much more selective in who they play, results often in those players lurking around, just waiting for "overvalued" opponents to try to challenge. Such players may feel discouraged of course from playing any significantly lower rated players again for rating concerns. And so, this is one possible anti-activity/anti-social aspect of the Elo rating system which needs to be understood. The agenda of points scoring can interfere with playing with abandon, and just for fun.[citation needed]
Interesting from the perspective of preserving high Elo ratings versus promoting rated game activity is a recent proposal by British Grandmaster John Nunn regarding qualifiers based on Elo rating for a World championship model.[13] Nunn highlights in the section on "Selection of players", that players not only be selected by high Elo ratings, but also their rated game activity. Nunn clearly separates the "activity bonus" from the Elo rating, and only implies using it as a tie-breaking mechanism.
The Elo system when applied to casual online servers has at least two other major practical issues that need tackling when Elo is applied to the context of online chess server ratings. These are engine abuse and selective pairing.[citation needed]
[edit] Chess engines
The first and most significant issue is players making use of chess engines to inflate their ratings. This is particularly an issue for correspondence chess style servers and organizations, where making use of a wide variety of engines within the same game is entirely possible. This would make any attempts to conclusively prove that someone is cheating quite futile. Blitz servers such as the Free Internet Chess Server or the Internet Chess Club attempt to minimize engine bias by clear indications that engine use is not allowed when logging on to their server.
[edit] Selective pairing
A more subtle issue is related to pairing. When players can choose their own opponents, they can choose opponents with minimal risk of losing, and maximum reward for winning. Such a luxury of being able to hand-pick your opponents is not present in Over-the-Board Elo type calculations, and therefore this may account strongly for the ratings on the ICC using Elo which are well over 2800.
Particular examples of 2800+ rated players choosing opponents with minimal risk and maximum possibility of rating gain include: choosing computers that they know they can beat with a certain strategy; choosing opponents that they think are over-rated; or avoiding playing strong players who are rated several hundred points below them, but may hold chess titles such as IM or GM. In the category of choosing over-rated opponents, new-entrants to the rating system who have played less than 50 games are in theory a convenient target as they may be overrated in their provisional rating. The ICC compensates for this issue by assigning a lower K-factor to the established player if they do win against a new rating entrant. The K-factor is actually a function of the number of rated games played by the new entrant.
Elo therefore must be treated as a bit of fun when applied in the context of online server ratings. Indeed the ability to choose one's own opponents can have great fun value also for spectators watching the very highest rated players. For example they can watch very strong GM's challenge other very strong GMs who are also rated over 3100. Such opposition, which the highest level players online would play in order to maintain their rating, would often be much stronger opponents than if they did play in an Open tournament which is run by Swiss pairings. Additionally it does help ensure that the game histories of those with very high ratings will often be with opponents of similarly high level ratings.
Therefore, Elo ratings online still provide a useful mechanism for providing a rating based on the opponent's rating. Its overall credibility, however, needs to be seen in the context of at least the above two major issues described — engine abuse, and selective pairing of opponents.
The ICC has also recently introduced "auto-pairing" ratings which are based on random pairings, but with each win in a row ensuring a statistically much harder opponent who has also won x games in a row. With potentially hundreds of players involved, this creates some of the challenges of a major large Swiss event which is being fiercely contested, with round winners meeting round winners. This approach to pairing certainly maximizes the rating risk of the higher-rated participants, who may face very stiff opposition from players below 3000 for example. This is a separate rating in itself, and is under "1-minute" and "5-minute" rating categories. Maximum ratings achieved over 2500 are exceptionally rare.
[edit] Ratings inflation and deflation
| This section does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (August 2007) |
| This section is written like a personal reflection or essay and may require cleanup. Please help improve it by rewriting it in an encyclopedic style. (March 2008) |
The primary goal of Elo ratings is to accurately predict game results between contemporary competitors, and FIDE ratings perform this task relatively well. A secondary, more ambitious goal is to use ratings to compare players between different eras. (See also Greatest chess player of all time.) It would be convenient if a FIDE rating of 2500 meant the same thing in 2005 that it meant in 1975. If the ratings suffer from inflation, then a modern rating of 2500 means less than a historical rating of 2500, while if the ratings suffer from deflation, the reverse will be true. Unfortunately, even among people who would like ratings from different eras to "mean the same thing", intuitions differ sharply as to whether a given rating should represent a fixed absolute skill or a fixed relative performance.
Those who believe in absolute skill (including FIDE[14]) would prefer modern ratings to be higher on average than historical ratings, if grandmasters nowadays are in fact playing better chess. By this standard, the rating system is functioning perfectly if a modern 2500-rated player and a 2500-rated player of another era would have equal chances of winning, were it possible for them to play. The advent of strong chess computers allows a somewhat objective evaluation of the absolute playing skill of past chess masters, based on their recorded games.
Those who believe in relative performance would prefer the median rating (or some other benchmark rank) of all eras to be the same. By one relative performance standard, the rating system is functioning perfectly if a player in the twentieth percentile of world rankings has the same rating as a player in the twentieth percentile used to have. Ratings should indicate approximately where a player stands in the chess hierarchy of his own era.
The average FIDE rating of top players has been steadily climbing for the past twenty years, which is inflation (and therefore undesirable) from the perspective of relative performance. However, it is at least plausible that FIDE ratings are not inflating in terms of absolute skill. Perhaps modern players are better than their predecessors due to a greater knowledge of openings and due to computer-assisted tactical training.
In any event, both camps can agree that it would be undesirable for the average rating of players to decline at all, or to rise faster than can be reasonably attributed to generally increasing skill. Both camps would call the former deflation and the latter inflation. Not only do rapid inflation and deflation make comparison between different eras impossible, they tend to introduce inaccuracies between more-active and less-active contemporaries.
The most straightforward attempt to avoid rating inflation/deflation is to have each game end in an equal transaction of rating points. If the winner gains N rating points, the loser should drop by N rating points. The intent is to keep the average rating constant, by preventing points from entering or leaving the system.
Unfortunately, this simple approach typically results in rating deflation, as the USCF was quick to discover.
A common misconception is that rating points enter the system every time a previously unrated player gets an initial rating and that likewise rating points leave the system every time someone retires from play. Players generally believe that since most players are significantly better at the end of their careers than at the beginning, that as they tend to take more points away from the system than they brought in, the system deflates as a result. This is a fallacy and is easily shown. If a system is deflated, players will have strengths higher than their ratings. But if they take points out of the system EQUAL TO their strength when they leave the system, no inflation or deflation will result.
Rather, in the "basic form" of the Elo system, the cause of deflation is the fact that players improve. The cause of inflation is that their strength relative to their rating will tend to decline over time with age. Since most players improve early in their career, the system tends to deflate at that time. Inflation doesn't occur until much later in a player's career. Many players will quit before this natural process occurs, which would return points to the system. The net result over time is deflation.
[edit] Example
The deflation can be shown via the following simplified example. Suppose there are four 1500-rated players: A, B, C, D, all established players with stable ratings. To make the calculations easy, we will assume that we will calculate rating changes under the old Elo formula with K=32. Elo recognized that simply having an improving player causes deflation.
Now, player A improves his chess skills to a degree that on average he scores 3 out of 4 against B, C, and D. These odds represent roughly a 200 rating point spread. If A, B, C and D are now in a tournament where they play 10 games against each opponent, A will win 22.5 of the 30 games. Players B, C and D will win 12.5 of their games. After the tournament, the players are given a new rating:
 ,
,
where W equals the number of wins and We equals the expected number of wins. Because prior to the tournament, all players had the same rating, they were expected to score 50%, so We = 15. Player A has a new rating of,
- (22.5 − 15.0)x32 + 1500 = 1740
so player A won 240 points, due to his increased chess skill. For B, C, D, the new rating is
- (12.5 − 15.0)x32 + 1500 = 1420,
so they all lost 80 points, even though their chess skill remained the same. It can be shown that if these four players continue playing games, without changing their chess skills, their final ratings will be
- A: 1700
- B: 1433
- C: 1433
- D: 1433,
so players B, C and D will have a lower rating, even if their skills did not decrease; the system is deflating.
[edit] Practical approaches
Because of the significant difference in timing of when inflation and deflation occur, and in order to combat deflation, most implementations of Elo ratings have a mechanism for injecting points into the system in order to maintain relative ratings over time. FIDE has two inflationary mechanisms. First, performances below a "ratings floor" are not tracked, so a player with true skill below the floor can only be unrated or overrated, never correctly rated. Second, established and higher-rated players have a lower K-factor.[10] There is no theoretical reason why these should provide a proper balance to an otherwise deflationary scheme; perhaps they over-correct and result in net inflation beyond the playing population's increase in absolute skill. On the other hand, there is no obviously superior alternative. In particular, on-line game rating systems have seemed to suffer at least as many inflation/deflation headaches as FIDE, despite alternative stabilization mechanisms.
[edit] Exponential variant
| This section may contain original research or unverified claims. Please improve the article by adding references. See the talk page for details. (December 2008) |
In many computer role-playing games, the played game character has an experience (which can be compared to the rating of a chess player), which grows exponentially as the character evolves (while the Elo rating of a chess player grows linear as the player evolves).[citation needed] Therefore, in a morpg with pairwise battles, it can be a desirable feature to have an experience attached to each character which resembles the Elo rating of a chess player, but grows exponentially to better match the experience of a character in other rpg's.
Let's call a character's experience Q, and define it as
where R would be the Elo rating of the character. We then have a bijection between R and P, where R = 400log10(Q / C). Notice that the experience will always be positive, while the rating can be any real number. Imagine we have two characters, A and B, with the experiences QA and QB. In a battle between A and B, the expected score of player A can be calculated using the exact formula
So, we have
and the corresponding expression for player B that is
When the battle is over, by using the formula for updating the rating of a character, we can also update the expereince of the character:
where F = 10K / 400. A low K values corresponds to an F values close to 1. However, while the K value is lower for stronger chess players, the F value is often left unchanged, to enable the system to be more dynamic (which is a requirement for making a game fun).[citation needed] In opposite to a chess player, a character of a single player rpg is made to evolve through out the entire game, as he encounters new and better items, develops his skills, learns new spells, etc. In a morpg on the other hand, the creators often continuously develop the games and create new patches, such as in World of Warcraft. As each patch is released, the environment of the game is changed; this makes the game more chaotic.
For low F values, the formula for updating the experience can be approximately estimated by
where  . Using players A and B as referrals again, and inserting the formula for the expected score, we can substitute E and obtain
. Using players A and B as referrals again, and inserting the formula for the expected score, we can substitute E and obtain
Now, since S = 1 at win, but 0 at loss, the experience gain is
[edit] Single player rpg's
In many single player rpg's, the character gets an experience boost when killing an enemy (i.e. a battle win). Since the character, A, often is considered to have much higher experience than an enemy, B, the experience gain when killing the enemy can be simplified to
An even simpler version of this would be to let the character's experience be the sum of the experience of all enemies it has killed (i.e. having κ = 1).
At death, many rpg's just let the player start over from the last visited status checkpoint.[citation needed] Having a single player rpg where the character loses experience each time it is killed would not be that sensible; firstly the chance of winning a battle is drastically decreased when fighting against more than one enemy at a time, hence making the expected score misleading. Besides, if the character would have it's experience decreased at each death, the average experience gain over a longer period of time would be around zero, which is not suitable for a single player rpg.
[edit] Other chess rating systems
- Ingo system, designed by Anton Hoesslinger, used in Germany 1948-1992 (Harkness 1967:205-6).
- Harkness System, invented by Kenneth Harkness, who published it in 1956 (Harkness 1967:185-88).
- British Chess Federation Rating System, published in 1958.
- Correspondence Chess League of America Rating System (now uses Elo).
- Glicko rating system
- Chessmetrics
- In November 2005, the Xbox Live online gaming service proposed the TrueSkill ranking system that is an extension of Glickman's system to multi-player and multi-team games.
[edit] Elo ratings in other games
National Scrabble organizations compute normally-distributed Elo ratings except in the United Kingdom, where a different system is used. The North American National Scrabble Association has the largest rated population, numbering over 11,000 as of early 2006. Lexulous also uses the Elo system.
The popular First Internet Backgammon Server calculates ratings based on a modified Elo system. New players are assigned a rating of 1500, with the best humans and bots rating over 2000. The same formula has been adopted by several other backgammon sites, such as Play65, DailyGammon, GoldToken and VogClub (Vinco Online Games). Vog sets a new player's rating at 1600.
The European Go Federation adopted an Elo based rating system initially pioneered by the Czech Go Federation.
In other sports, individuals maintain rankings based on the Elo algorithm. These are usually unofficial, not endorsed by the sport's governing body. The World Football Elo Ratings rank national teams in men's football (soccer). Jeff Sagarin publishes team rankings for American college football and basketball, with "Elo chess" being one of the two rankings he presents. In 2006, Elo ratings were adapted for Major League Baseball teams by Nate Silver of Baseball Prospectus.[15] Based on this adaptation, Baseball Prospectus also makes Elo-based Monte Carlo simulations of the odds of whether teams will make the playoffs.[16] Glenn O'Brien publishes team rankings for Hopman Cup using several rating systems, including variants of the Elo rating system.[17] One of the few Elo-based rankings endorsed by a sport's governing body is the FIFA Women's World Rankings, based on a simplified version of the Elo algorithm, which FIFA uses as its official ranking system for national teams in women's football (soccer).
In the strategy game Tantrix an Elo-rating scored in a tournament changes the overall rating according to the ratio of the games played in the tournament and the overall game count. Every year passed, ratings are deweighted until they completely disappear taken over by the new ratings.[18] In the strategy game Arimaa an Elo-type rating system is used. In this rating system, however, there is a second parameter "rating uncertainty", which doubles as the K-factor.[19]
Various online roleplaying-games (MMORPGs) use Elo ratings for player-vs-player (PVP) rankings. In Guild Wars, Elo ratings are used to record guild rating gained and lost through Guild versus Guild battles, which are two-team fights. The K-value, as of December 2006, is 30, but will change to 5 shortly into the year 2007. Vendetta Online uses Elo ratings to rank the flight combat skill of players when they have agreed to a 1-on-1 duel. World of Warcraft uses the Elo Rating system when teaming up and comparing Arena players.[20] The game Puzzle Pirates uses the ELO rating system as well to determine the standings in the various puzzles.
Trading-card game manufacturers often use Elo ratings for their organized play efforts. The DCI (formerly Duelists' Convocation International) uses Elo ratings for tournaments of Magic: The Gathering and other games of Wizards of the Coast. Pokémon USA uses the Elo system to rank its TCG organised play competitors. Prizes for the top players in various regions include holidays and world championships invites. Similarly, Decipher, Inc. used the Elo system for its ranked games such as Star Trek Customizable Card Game and Star Wars Customizable Card Game.
FoosballRankings.com has applied the Elo Rating System to the game of foosball by offering a free Elo ranking tool that can be used in Foosball tournaments and leagues. The ranking tool can even be modified by the players so that they have more control over the math behind it.
WeeWar uses a modified Elo Rating System to rank the players of its online turn based strategy game. The only difference is that rankings are unaffected by a draw.
TotoScacco uses a modified Elo rating system to rank the players of its guess-the-results game, where one has to predict the results of top chess events.
Golden Tee Golf uses an ELO rating system. Generally, any rating of 3000 or higher, the player is considered one of the elite of the game. This player usually places top 3 in tournaments on a regular basis. A rating of 2900-2999, this player will generally score in the top 5 with top 3 finishes about 60% of the time. A rating between 2750-2900, this player will score top 10 on a regular basis with a top 5 finish 40-50% of the time and a top 3 finish 20% of the time. A rating of 2750 and below, the player will generally finish in the top 20 on a regular basis, the top 10 on a 40%-50% basis, the top 5 on a 15% basis and will finish in the top 3 on a 5% basis.
theBlitz wargaming club uses a modified Elo rating system for a number of computer strategy games. The main modification was implemented to accurately reflect different levels of victory. For example, in John Tiller's Campaign Series, there are five victory levels: Major Win, Minor Win, Draw, Minor Loss, Major Loss.
- Age of Empires III[21]
- Age of Mythology[citation needed]
- Battlefield Heroes [22][citation needed]
- Chaotic Trading Card Game[citation needed]
- Close Combat series
- Command & Conquer 3: Tiberium Wars[citation needed]
- Conquest
- Diablo II[citation needed]
- Duels[23]
- Forces
- Gears of War 2[24]
- Guild Wars[25]
- Guitar Hero III: Legends of Rock[26]
- Halo 2[27]
- iRacing[citation needed]
- Kiekko.tk[citation needed]
- Magic: The Gathering[28]
- Pro Cycling Manager Season 2007[citation needed]
- Quake III Arena DeFRaG[29]
- Rainbow Six 3: Raven Shield[citation needed]
- Scrabulous[30]
- Soldat (Zitro-Stats)[31]
- StarCraft[32]
- Star Wars Customizable Card Game (under Decipher's control)[citation needed]
- Star Wars Battlefront[citation needed]
- Supreme Commander (uses a modified version of Elo)[33]
- Taikodom[34]
- Tantrix[35]
- Toribash[citation needed]
- Unreal Tournament 2004[citation needed]
- Unreal Tournament 3[citation needed]
- Urban Rivals[36]
- Warcraft III[citation needed]
- World of Warcraft[37]
- Yahoo Pool[citation needed]
[edit] See also
[edit] Notes
- ^ Redman, Tim. "Remembering Richard, Part II". United States Chess Federation. http://www.uschess.org/ratings/RedmanremembersRichard.pdf.
- ^ "About the USCF". United States Chess Federation. http://www.uschess.org/about/about.php. Retrieved on 2008-11-10.
- ^ World Chess Championship in Mexico reaches Category XXI, official web site of the World Chess Championship 2007
- ^ Anand lost #1 to Morozevich (Chessbase, August 24 2008), then regained it, then Carlsen took #1 (Chessbase, September 5 2008), then Ivanchuk (Chessbase, September 11 2008), and finally Topalov (Chessbase, September 13 2008)
- ^ US Chess Federation:
- ^ "Approximating Formulas for the USCF Rating System", United States Chess Federation, Mark Glickman, Department of Mathematics and Statistics at Boston University, 22 February 2001
- ^ For instance, see the comments at ChessBase.com - Chess News - Adams vs Hydra: Man 0.5 – Machine 5.5
- ^ Chessbase article
- ^ A key Sonas article is Jeff Sonas: The Sonas Rating Formula — Better than Elo?
- ^ a b FIDE Online. FIDE Handbook: Chess rules
- ^ ICC Help: k-factor
- ^ A Parent's Guide to Chess Skittles, Don Heisman, Chesscafe.com, August 4, 2002
- ^ ChessBase.com - Chess News - The Nunn Plan for the World Chess Championship
- ^ FIDE Online. FIDE Handbook: Chess rules
- ^ Nate Silver, "We Are Elo?" June 28, 2006.[1]
- ^ Postseason Odds, ELO version
- ^ Glenn O'Brien's ratings page
- ^ http://tournaments.tantrix.co.uk/ratings/rating.shtml
- ^ Arimaa Rating System
- ^ World of Warcraft Europe -> The Arena
- ^ AOE3 ELO Rating
- ^ [2]
- ^ Duels
- ^ [3]
- ^ Guild ladder - Guild Wars Wiki (GWW)
- ^ Guitar Hero Community - Forum Topics
- ^ Bungie.net : Bungie Online : Halo 2 Stats Info : Halo 2 Overview
- ^ DCI Universal Tournament Rules
- ^ www.q3df.org
- ^ Connexion | Facebook
- ^ Message shown at "history" pages: "In History you can see all Actions from Servers and track Points. They are calculated by Killer's and Victim's Points with this Elo-Formula: [4] (source: http://zitrostats.rumpelful.de/?inc=history)
- ^ TeamLiquid.net professional gamer rankings
- ^ GPGNet / SupCom FAQ
- ^ Taikodom Ratings System
- ^ Tantrix ratings
- ^ [5]
- ^ World of Warcraft Arena system
[edit] References
- Elo, Arpad (1978). The Rating of Chessplayers, Past and Present. Arco. ISBN 0-668-04721-6.
- Harkness, Kenneth (1967), Official Chess Handbook, McKay
[edit] External links
- Official FIDE Rating List
- All Time Rankings - lists the top 10 from 1970 to 1997
- Unofficial Live Top List
- Arpad Emre Elo – 100th anniversary
- GoBase.org: Introduction to the Elo Rating System
- Citations for Elo, A.E. 1978. The Ratings of Chess Players: Past and Present.
- Mark Glickman's research page, with a number of links to technical papers on chess rating systems
- Bayesian Elo Rating
- http://chess.about.com/library/weekly/aa03a25.htm
- Professional foosball players are ranked using Elo. Includes interesting adjustments for doubles.
- A site that ranks national soccer teams using Elo methods
- An attempt to apply ELO rating to Bao
- EGF Official Ratings
- Jeff Sonas: The Sonas Rating Formula — Better than Elo?
- Elo query with world ranking list and historical development since 1990
- National Scrabble Association ratings
- The Elo-rating system used for Tantrix
- Popular Elo rating system for Age of Empires 3 computer game
- US Squash National Rankings
- Chess Rankings Website uses Elo to rank players online.
- Elo ratings applied to race car drivers.