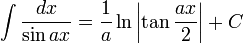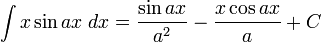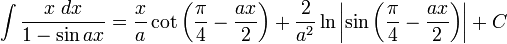List of integrals of trigonometric functions

	Trigonometry
	History; Usage; Functions; Inverse functions; Further reading;
	Reference
	List of identities; Exact constants; Generating trigonometric tables; CORDIC
	Euclidean theory
	Law of sines; Law of cosines; Law of tangents; Pythagorean theorem
	Calculus
	The Trigonometric integral; Trigonometric substitution; Integrals of functions; Derivatives of functions; Integrals of inverses;

From Wikipedia, the free encyclopedia

Jump to: navigation, search

The following is a list of integrals (antiderivative functions) of trigonometric functions. For antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functions. For a complete list of antiderivative functions, see lists of integrals. See also trigonometric integral.

In all formulas the constant a is assumed to be nonzero, and C denotes the constant of integration.

1 Antiderivatives containing only sine
2 Antiderivatives containing only cosine
3 Antiderivatives containing only tangent
4 Antiderivatives containing only secant
5 Antiderivatives containing only cosecant
6 Antiderivatives containing only cotangent
7 Antiderivatives containing both sine and cosine
8 Antiderivatives containing both sine and tangent
9 Antiderivatives containing both cosine and tangent
10 Antiderivatives containing both sine and cotangent
11 Antiderivatives containing both cosine and cotangent
12 Antiderivatives with symmetric limits

[edit] Antiderivatives containing only sine

$\int\sin ax\;dx = -\frac{1}{a}\cos ax+C\,\!$

$\int\sin^2 {ax}\;dx = \frac{x}{2} - \frac{1}{4a} \sin 2ax +C= \frac{x}{2} - \frac{1}{2a} \sin ax\cos ax +C\!$

$\int x\sin^2 {ax}\;dx = \frac{x^2}{4} - \frac{x}{4a} \sin 2ax - \frac{1}{8a^2} \cos 2ax +C\!$

$\int x^2\sin^2 {ax}\;dx = \frac{x^3}{6} - \left( \frac {x^2}{4a} - \frac{1}{8a^3} \right) \sin 2ax - \frac{x}{4a^2} \cos 2ax +C\!$

$\int\sin b_1x\sin b_2x\;dx = \frac{\sin((b_1-b_2)x)}{2(b_1-b_2)}-\frac{\sin((b_1+b_2)x)}{2(b_1+b_2)}+C \qquad\mbox{(for }|b_1|\neq|b_2|\mbox{)}\,\!$

$\int\sin^n {ax}\;dx = -\frac{\sin^{n-1} ax\cos ax}{na} + \frac{n-1}{n}\int\sin^{n-2} ax\;dx \qquad\mbox{(for }n>0\mbox{)}\,\!$

$\int\frac{dx}{\sin ax} = \frac{1}{a}\ln \left|\tan\frac{ax}{2}\right|+C$

$\int\frac{dx}{\sin^n ax} = \frac{\cos ax}{a(1-n) \sin^{n-1} ax}+\frac{n-2}{n-1}\int\frac{dx}{\sin^{n-2}ax} \qquad\mbox{(for }n>1\mbox{)}\,\!$

$\int x\sin ax\;dx = \frac{\sin ax}{a^2}-\frac{x\cos ax}{a}+C\,\!$

$\int x^n\sin ax\;dx = -\frac{x^n}{a}\cos ax+\frac{n}{a}\int x^{n-1}\cos ax\;dx \qquad\mbox{(for }n>0\mbox{)}\,\!$

$\int_{\frac{-a}{2}}^{\frac{a}{2}} x^2\sin^2 {\frac{n\pi x}{a}}\;dx = \frac{a^3(n^2\pi^2-6)}{24n^2\pi^2} \qquad\mbox{(for }n=2,4,6...\mbox{)}\,\!$

$\int\frac{\sin ax}{x} dx = \sum_{n=0}^\infty (-1)^n\frac{(ax)^{2n+1}}{(2n+1)\cdot (2n+1)!} +C\,\!$

$\int\frac{\sin ax}{x^n} dx = -\frac{\sin ax}{(n-1)x^{n-1}} + \frac{a}{n-1}\int\frac{\cos ax}{x^{n-1}} dx\,\!$

$\int\frac{dx}{1\pm\sin ax} = \frac{1}{a}\tan\left(\frac{ax}{2}\mp\frac{\pi}{4}\right)+C$

$\int\frac{x\;dx}{1+\sin ax} = \frac{x}{a}\tan\left(\frac{ax}{2} - \frac{\pi}{4}\right)+\frac{2}{a^2}\ln\left|\cos\left(\frac{ax}{2}-\frac{\pi}{4}\right)\right|+C$

$\int\frac{x\;dx}{1-\sin ax} = \frac{x}{a}\cot\left(\frac{\pi}{4} - \frac{ax}{2}\right)+\frac{2}{a^2}\ln\left|\sin\left(\frac{\pi}{4}-\frac{ax}{2}\right)\right|+C$

$\int\frac{\sin ax\;dx}{1\pm\sin ax} = \pm x+\frac{1}{a}\tan\left(\frac{\pi}{4}\mp\frac{ax}{2}\right)+C$

[edit] Antiderivatives containing only cosine

$\int\cos ax\;dx = \frac{1}{a}\sin ax+C\,\!$

$\int\cos^n ax\;dx = \frac{\cos^{n-1} ax\sin ax}{na} + \frac{n-1}{n}\int\cos^{n-2} ax\;dx \qquad\mbox{(for }n>0\mbox{)}\,\!$

$\int x\cos ax\;dx = \frac{\cos ax}{a^2} + \frac{x\sin ax}{a}+C\,\!$

$\int\cos^2 {ax}\;dx = \frac{x}{2} + \frac{1}{4a} \sin 2ax +C = \frac{x}{2} + \frac{1}{2a} \sin ax\cos ax +C\!$

$\int x^2\cos^2 {ax}\;dx = \frac{x^3}{6} + \left( \frac {x^2}{4a} - \frac{1}{8a^3} \right) \sin 2ax + \frac{x}{4a^2} \cos 2ax +C\!$

$\int x^n\cos ax\;dx = \frac{x^n\sin ax}{a} - \frac{n}{a}\int x^{n-1}\sin ax\;dx\,\!$

$\int_{\frac{-a}{2}}^{\frac{a}{2}} x^2\cos^2 {\frac{n\pi x}{a}}\;dx = \frac{a^3(n^2\pi^2-6)}{24n^2\pi^2} \qquad\mbox{(for }n=1,3,5...\mbox{)}\,\!$

$\int\frac{\cos ax}{x} dx = \ln|ax|+\sum_{k=1}^\infty (-1)^k\frac{(ax)^{2k}}{2k\cdot(2k)!}+C\,\!$

$\int\frac{\cos ax}{x^n} dx = -\frac{\cos ax}{(n-1)x^{n-1}}-\frac{a}{n-1}\int\frac{\sin ax}{x^{n-1}} dx \qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{dx}{\cos ax} = \frac{1}{a}\ln\left|\tan\left(\frac{ax}{2}+\frac{\pi}{4}\right)\right|+C$

$\int\frac{dx}{\cos^n ax} = \frac{\sin ax}{a(n-1) \cos^{n-1} ax} + \frac{n-2}{n-1}\int\frac{dx}{\cos^{n-2} ax} \qquad\mbox{(for }n>1\mbox{)}\,\!$

$\int\frac{dx}{1+\cos ax} = \frac{1}{a}\tan\frac{ax}{2}+C\,\!$

$\int\frac{dx}{1-\cos ax} = -\frac{1}{a}\cot\frac{ax}{2}+C\,\!$

$\int\frac{x\;dx}{1+\cos ax} = \frac{x}{a}\tan\frac{ax}{2} + \frac{2}{a^2}\ln\left|\cos\frac{ax}{2}\right|+C$

$\int\frac{x\;dx}{1-\cos ax} = -\frac{x}{a}\cot\frac{ax}{2}+\frac{2}{a^2}\ln\left|\sin\frac{ax}{2}\right|+C$

$\int\frac{\cos ax\;dx}{1+\cos ax} = x - \frac{1}{a}\tan\frac{ax}{2}+C\,\!$

$\int\frac{\cos ax\;dx}{1-\cos ax} = -x-\frac{1}{a}\cot\frac{ax}{2}+C\,\!$

$\int\cos a_1x\cos a_2x\;dx = \frac{\sin(a_1-a_2)x}{2(a_1-a_2)}+\frac{\sin(a_1+a_2)x}{2(a_1+a_2)}+C \qquad\mbox{(for }|a_1|\neq|a_2|\mbox{)}\,\!$

[edit] Antiderivatives containing only tangent

$\int\tan ax\;dx = -\frac{1}{a}\ln|\cos ax|+C = \frac{1}{a}\ln|\sec ax|+C\,\!$

$\int\tan^n ax\;dx = \frac{1}{a(n-1)}\tan^{n-1} ax-\int\tan^{n-2} ax\;dx \qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{dx}{q \tan ax + p} = \frac{1}{p^2 + q^2}(px + \frac{q}{a}\ln|q\sin ax + p\cos ax|)+C \qquad\mbox{(for }p^2 + q^2\neq 0\mbox{)}\,\!$

$\int\frac{dx}{\tan ax} = \frac{1}{a}\ln|\sin ax|+C\,\!$

$\int\frac{dx}{\tan ax + 1} = \frac{x}{2} + \frac{1}{2a}\ln|\sin ax + \cos ax|+C\,\!$

$\int\frac{dx}{\tan ax - 1} = -\frac{x}{2} + \frac{1}{2a}\ln|\sin ax - \cos ax|+C\,\!$

$\int\frac{\tan ax\;dx}{\tan ax + 1} = \frac{x}{2} - \frac{1}{2a}\ln|\sin ax + \cos ax|+C\,\!$

$\int\frac{\tan ax\;dx}{\tan ax - 1} = \frac{x}{2} + \frac{1}{2a}\ln|\sin ax - \cos ax|+C\,\!$

[edit] Antiderivatives containing only secant

$\int \sec{ax} \, dx = \frac{1}{a}\ln{\left| \sec{ax} + \tan{ax}\right|}+C$

$\int \sec^n{ax} \, dx = \frac{\sec^{n-1}{ax} \sin {ax}}{a(n-1)} \,+\, \frac{n-2}{n-1}\int \sec^{n-2}{ax} \, dx \qquad \mbox{ (for }n \ne 1\mbox{)}\,\!$

$\int \sec^n{x} \, dx = \frac{\sec^{n-2}{x}\tan{x}}{n-1} \,+\, \frac{n-2}{n-1}\int \sec^{n-2}{x}\,dx$ ^[1]

$\int \frac{dx}{\sec{x} + 1} = x - \tan{\frac{x}{2}}+C$

[edit] Antiderivatives containing only cosecant

$\int \csc{ax} \, dx = \frac{1}{a}\ln{\left| \csc{ax} - \cot{ax}\right|}+C$

$\int \csc^2{x} \, dx = -\cot{x}+C$

$\int \csc^n{ax} \, dx = -\frac{\csc^{n-1}{ax} \cos{ax}}{a(n-1)} \,+\, \frac{n-2}{n-1}\int \csc^{n-2}{ax} \, dx \qquad \mbox{ (for }n \ne 1\mbox{)}\,\!$

[edit] Antiderivatives containing only cotangent

$\int\cot ax\;dx = \frac{1}{a}\ln|\sin ax|+C\,\!$

$\int\cot^n ax\;dx = -\frac{1}{a(n-1)}\cot^{n-1} ax - \int\cot^{n-2} ax\;dx \qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{dx}{1 + \cot ax} = \int\frac{\tan ax\;dx}{\tan ax+1}\,\!$

$\int\frac{dx}{1 - \cot ax} = \int\frac{\tan ax\;dx}{\tan ax-1}\,\!$

[edit] Antiderivatives containing both sine and cosine

$\int\frac{dx}{\cos ax\pm\sin ax} = \frac{1}{a\sqrt{2}}\ln\left|\tan\left(\frac{ax}{2}\pm\frac{\pi}{8}\right)\right|+C$

$\int\frac{dx}{(\cos ax\pm\sin ax)^2} = \frac{1}{2a}\tan\left(ax\mp\frac{\pi}{4}\right)+C$

$\int\frac{dx}{(\cos x + \sin x)^n} = \frac{1}{n-1}\left(\frac{\sin x - \cos x}{(\cos x + \sin x)^{n - 1}} - 2(n - 2)\int\frac{dx}{(\cos x + \sin x)^{n-2}} \right)$

$\int\frac{\cos ax\;dx}{\cos ax + \sin ax} = \frac{x}{2} + \frac{1}{2a}\ln\left|\sin ax + \cos ax\right|+C$

$\int\frac{\cos ax\;dx}{\cos ax - \sin ax} = \frac{x}{2} - \frac{1}{2a}\ln\left|\sin ax - \cos ax\right|+C$

$\int\frac{\sin ax\;dx}{\cos ax + \sin ax} = \frac{x}{2} - \frac{1}{2a}\ln\left|\sin ax + \cos ax\right|+C$

$\int\frac{\sin ax\;dx}{\cos ax - \sin ax} = -\frac{x}{2} - \frac{1}{2a}\ln\left|\sin ax - \cos ax\right|+C$

$\int\frac{\cos ax\;dx}{\sin ax(1+\cos ax)} = -\frac{1}{4a}\tan^2\frac{ax}{2}+\frac{1}{2a}\ln\left|\tan\frac{ax}{2}\right|+C$

$\int\frac{\cos ax\;dx}{\sin ax(1+-\cos ax)} = -\frac{1}{4a}\cot^2\frac{ax}{2}-\frac{1}{2a}\ln\left|\tan\frac{ax}{2}\right|+C$

$\int\frac{\sin ax\;dx}{\cos ax(1+\sin ax)} = \frac{1}{4a}\cot^2\left(\frac{ax}{2}+\frac{\pi}{4}\right)+\frac{1}{2a}\ln\left|\tan\left(\frac{ax}{2}+\frac{\pi}{4}\right)\right|+C$

$\int\frac{\sin ax\;dx}{\cos ax(1-\sin ax)} = \frac{1}{4a}\tan^2\left(\frac{ax}{2}+\frac{\pi}{4}\right)-\frac{1}{2a}\ln\left|\tan\left(\frac{ax}{2}+\frac{\pi}{4}\right)\right|+C$

$\int\sin ax\cos ax\;dx = \frac{1}{2a}\sin^2 ax +C\,\!$

$\int\sin a_1x\cos a_2x\;dx = -\frac{\cos(a_1+a_2)x}{2(a_1+a_2)}-\frac{\cos(a_1-a_2)x}{2(a_1-a_2)} +C\qquad\mbox{(for }|a_1|\neq|a_2|\mbox{)}\,\!$

$\int\sin^n ax\cos ax\;dx = \frac{1}{a(n+1)}\sin^{n+1} ax +C\qquad\mbox{(for }n\neq -1\mbox{)}\,\!$

$\int\sin ax\cos^n ax\;dx = -\frac{1}{a(n+1)}\cos^{n+1} ax +C\qquad\mbox{(for }n\neq -1\mbox{)}\,\!$

$\int\sin^n ax\cos^m ax\;dx = -\frac{\sin^{n-1} ax\cos^{m+1} ax}{a(n+m)}+\frac{n-1}{n+m}\int\sin^{n-2} ax\cos^m ax\;dx \qquad\mbox{(for }m,n>0\mbox{)}\,\!$

also: $\int\sin^n ax\cos^m ax\;dx = \frac{\sin^{n+1} ax\cos^{m-1} ax}{a(n+m)} + \frac{m-1}{n+m}\int\sin^n ax\cos^{m-2} ax\;dx \qquad\mbox{(for }m,n>0\mbox{)}\,\!$

$\int\frac{dx}{\sin ax\cos ax} = \frac{1}{a}\ln\left|\tan ax\right|+C$

$\int\frac{dx}{\sin ax\cos^n ax} = \frac{1}{a(n-1)\cos^{n-1} ax}+\int\frac{dx}{\sin ax\cos^{n-2} ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{dx}{\sin^n ax\cos ax} = -\frac{1}{a(n-1)\sin^{n-1} ax}+\int\frac{dx}{\sin^{n-2} ax\cos ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{\sin ax\;dx}{\cos^n ax} = \frac{1}{a(n-1)\cos^{n-1} ax} +C\qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{\sin^2 ax\;dx}{\cos ax} = -\frac{1}{a}\sin ax+\frac{1}{a}\ln\left|\tan\left(\frac{\pi}{4}+\frac{ax}{2}\right)\right|+C$

$\int\frac{\sin^2 ax\;dx}{\cos^n ax} = \frac{\sin ax}{a(n-1)\cos^{n-1}ax}-\frac{1}{n-1}\int\frac{dx}{\cos^{n-2}ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{\sin^n ax\;dx}{\cos ax} = -\frac{\sin^{n-1} ax}{a(n-1)} + \int\frac{\sin^{n-2} ax\;dx}{\cos ax} \qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{\sin^n ax\;dx}{\cos^m ax} = \frac{\sin^{n+1} ax}{a(m-1)\cos^{m-1} ax}-\frac{n-m+2}{m-1}\int\frac{\sin^n ax\;dx}{\cos^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!$

also: $\int\frac{\sin^n ax\;dx}{\cos^m ax} = -\frac{\sin^{n-1} ax}{a(n-m)\cos^{m-1} ax}+\frac{n-1}{n-m}\int\frac{\sin^{n-2} ax\;dx}{\cos^m ax} \qquad\mbox{(for }m\neq n\mbox{)}\,\!$

also: $\int\frac{\sin^n ax\;dx}{\cos^m ax} = \frac{\sin^{n-1} ax}{a(m-1)\cos^{m-1} ax}-\frac{n-1}{m-1}\int\frac{\sin^{n-2} ax\;dx}{\cos^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!$

$\int\frac{\cos ax\;dx}{\sin^n ax} = -\frac{1}{a(n-1)\sin^{n-1} ax} +C\qquad\mbox{(for }n\neq 1\mbox{)}\,\!$

$\int\frac{\cos^2 ax\;dx}{\sin ax} = \frac{1}{a}\left(\cos ax+\ln\left|\tan\frac{ax}{2}\right|\right) +C$

$\int\frac{\cos^2 ax\;dx}{\sin^n ax} = -\frac{1}{n-1}\left(\frac{\cos ax}{a\sin^{n-1} ax)}+\int\frac{dx}{\sin^{n-2} ax}\right) \qquad\mbox{(for }n\neq 1\mbox{)}$

$\int\frac{\cos^n ax\;dx}{\sin^m ax} = -\frac{\cos^{n+1} ax}{a(m-1)\sin^{m-1} ax} - \frac{n-m-2}{m-1}\int\frac{\cos^n ax\;dx}{\sin^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!$

also: $\int\frac{\cos^n ax\;dx}{\sin^m ax} = \frac{\cos^{n-1} ax}{a(n-m)\sin^{m-1} ax} + \frac{n-1}{n-m}\int\frac{\cos^{n-2} ax\;dx}{\sin^m ax} \qquad\mbox{(for }m\neq n\mbox{)}\,\!$

also: $\int\frac{\cos^n ax\;dx}{\sin^m ax} = -\frac{\cos^{n-1} ax}{a(m-1)\sin^{m-1} ax} - \frac{n-1}{m-1}\int\frac{\cos^{n-2} ax\;dx}{\sin^{m-2} ax} \qquad\mbox{(for }m\neq 1\mbox{)}\,\!$