Canny edge detector
From Wikipedia, the free encyclopedia
| Feature detection | |
 Output of a typical corner detection algorithm |
|
| Edge detection | |
|---|---|
| Canny | |
| Canny-Deriche | |
| Differential | |
| Sobel | |
| Interest point detection | |
| Corner detection | |
| Harris operator | |
| Shi and Tomasi | |
| Level curve curvature | |
| SUSAN | |
| FAST | |
| Blob detection | |
| Laplacian of Gaussian (LoG) | |
| Difference of Gaussians (DoG) | |
| Determinant of Hessian (DoH) | |
| Maximally stable extremal regions | |
| Ridge detection | |
| Affine invariant feature detection | |
| Affine shape adaptation | |
| Harris affine | |
| Hessian affine | |
| Feature description | |
| SIFT | |
| SURF | |
| GLOH | |
| LESH | |
| Scale-space | |
| Scale-space axioms | |
| Implementation details | |
| Pyramids | |
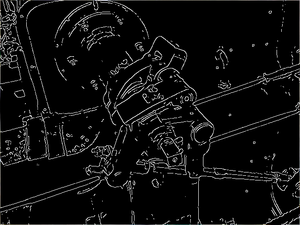
The Canny edge detection operator was developed by John F. Canny in 1986 and uses a multi-stage algorithm to detect a wide range of edges in images. Most importantly, Canny also produced a computational theory of edge detection explaining why the technique works.
Contents |
[edit] Development of the Canny algorithm
Canny's aim was to discover the optimal edge detection algorithm. In this situation, an "optimal" edge detector means:
- good detection - the algorithm should mark as many real edges in the image as possible.
- good localization - edges marked should be as close as possible to the edge in the real image.
- minimal response - a given edge in the image should only be marked once, and where possible, image noise should not create false edges.
To satisfy these requirements Canny used the calculus of variations - a technique which finds the function which optimizes a given functional. The optimal function in Canny's detector is described by the sum of four exponential terms, but can be approximated by the first derivative of a Gaussian.
[edit] Stages of the Canny algorithm
[edit] Noise reduction
Because the Canny edge detector uses a filter based on the first derivative of a Gaussian, it is susceptible to noise present on raw unprocessed image data, so to begin with, the raw image is convolved with a Gaussian filter. The result is a slightly blurred version of the original which is not affected by a single noisy pixel to any significant degree.
Here is an example of a 5x5 Gaussian filter, used to create the image to the right, with σ = 1.4:
[edit] Finding the intensity gradient of the image
An edge in an image may point in a variety of directions, so the Canny algorithm uses four filters to detect horizontal, vertical and diagonal edges in the blurred image. The edge detection operator (Roberts, Prewitt, Sobel for example) returns a value for the first derivative in the horizontal direction (Gy) and the vertical direction (Gx). From this the edge gradient and direction can be determined:
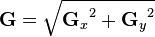

The edge direction angle is rounded to one of four angles representing vertical, horizontal and the two diagonals (0, 45, 90 and 135 degrees for example).
[edit] Non-maximum suppression
Given estimates of the image gradients, a search is then carried out to determine if the gradient magnitude assumes a local maximum in the gradient direction. So, for example,
- if the rounded angle is zero degrees the point will be considered to be on the edge if its intensity is greater than the intensities in the north and south directions,
- if the rounded angle is 90 degrees the point will be considered to be on the edge if its intensity is greater than the intensities in the west and east directions,
- if the rounded angle is 135 degrees the point will be considered to be on the edge if its intensity is greater than the intensities in the north east and south west directions,
- if the rounded angle is 45 degrees the point will be considered to be on the edge if its intensity is greater than the intensities in the north west and south east directions.
This is worked out by passing a 3x3 grid over the intensity map.
From this stage referred to as non-maximum suppression, a set of edge points, in the form of a binary image, is obtained. These are sometimes referred to as "thin edges".
[edit] Tracing edges through the image and hysteresis thresholding
Intensity gradients which are large are more likely to correspond to edges than if they are small. It is in most cases impossible to specify a threshold at which a given intensity gradient switches from corresponding to an edge into not doing so. Therefore Canny uses thresholding with hysteresis.
Thresholding with hysteresis requires two thresholds - high and low. Making the assumption that important edges should be along continuous curves in the image allows us to follow a faint section of a given line and to discard a few noisy pixels that do not constitute a line but have produced large gradients. Therefore we begin by applying a high threshold. This marks out the edges we can be fairly sure are genuine. Starting from these, using the directional information derived earlier, edges can be traced through the image. While tracing an edge, we apply the lower threshold, allowing us to trace faint sections of edges as long as we find a starting point.
Once this process is complete we have a binary image where each pixel is marked as either an edge pixel or a non-edge pixel. From complementary output from the edge tracing step, the binary edge map obtained in this way can also be treated as a set of edge curves, which after further processing can be represented as polygons in the image domain.
[edit] Differential geometric formulation of the Canny edge detector
A more refined approach to obtain edges with sub-pixel accuracy is by using the approach of differential edge detection, where the requirement of non-maximum suppression is formulated in terms of second- and third-order derivatives computed from a scale-space representation (Lindeberg 1998) -- see the article on edge detection for a detailed description.
[edit] Parameters
The Canny algorithm contains a number of adjustable parameters, which can affect the computation time and effectiveness of the algorithm.
- The size of the Gaussian filter: the smoothing filter used in the first stage directly affects the results of the Canny algorithm. Smaller filters cause less blurring, and allow detection of small, sharp lines. A larger filter causes more blurring, smearing out the value of a given pixel over a larger area of the image. Larger blurring radii are more useful for detecting larger, smoother edges - for instance, the edge of a rainbow.
- Thresholds: the use of two thresholds with hysteresis allows more flexibility than in a single-threshold approach, but general problems of thresholding approaches still apply. A threshold set too high can miss important information. On the other hand, a threshold set too low will falsely identify irrelevant information (such as noise) as important. It is difficult to give a generic threshold that works well on all images. No tried and tested approach to this problem yet exists.
[edit] Conclusion
The Canny algorithm is adaptable to various environments. Its parameters allow it to be tailored to recognition of edges of differing characteristics depending on the particular requirements of a given implementation. In Canny's original paper, the derivation of the optimal filter led to a Finite Impulse Response filter, which can be slow to compute in the spatial domain if the amount of smoothing required is important (the filter will have a large spatial support in that case). For this reason, it is often suggested to use Rachid Deriche's Infinite Impulse Response form of Canny's filter (the Canny-Deriche detector), which is recursive, and which can be computed in a short, fixed amount of time for any desired amount of smoothing. The second form is suitable for real time implementations in FPGAs or DSPs, or very fast embedded PCs. In this context, however, the regular recursive implementation of the Canny operator does not give a good approximation of rotational symmetry and therefore gives a bias towards horizontal and vertical edges.
[edit] References
- Canny, J., A Computational Approach To Edge Detection, IEEE Trans. Pattern Analysis and Machine Intelligence, 8:679-714, 1986.
- R. Deriche, Using Canny's criteria to derive an optimal edge detector recursively implemented, Int. J. Computer Vision, Vol. 1, pp. 167-187, April 1987.
- Lindeberg, Tony "Edge detection and ridge detection with automatic scale selection", International Journal of Computer Vision, 30, 2, pp 117--154, 1998. (Includes the differential approach to non-maximum suppression.)
[edit] See also
- Edge detection
- Feature detection (computer vision)
- Feature extraction
- Scale space
- Ridge detection
- Computer vision
- Digital image processing





