definition emgraçado evolu%C3%A7%C3%A3oconceitosmatematicos firefox:bookmarks iso matematikk math math, mathematics maths mathsemb notation signs sitesem standard studie symbol symbols usefultool/mathematics 수학 수학기호
ISO 31-11
From Wikipedia, the free encyclopedia
| This article contains special characters. Without proper rendering support, you may see question marks, boxes, or other symbols. |
ISO 31-11 is the part of international standard ISO 31 that defines mathematical signs and symbols for use in physical sciences and technology.
Its definitions include:[1]
Contents |
[edit] Mathematical logic
| Sign | Example | Name | Meaning and verbal equivalent | Remarks |
|---|---|---|---|---|
| ∧ | p ∧ q | conjunction sign | p and q | |
| ∨ | p ∨ q | disjunction sign | p or q (or both) | |
| ¬ | ¬ p | negation sign | negation of p; not p; non p | |
| ⇒ | p ⇒ q | implication sign | if p then q; p implies q | Can also be written as q ⇐ p. Sometimes → is used. |
| ∀ | ∀x∈A p(x) (∀x∈A) p(x) |
universal quantifier | for every x belonging to A, the proposition p(x) is true | The "∈A" can be dropped where A is clear from context. |
| ∃ | ∃x∈A p(x) (∃x∈A) p(x) |
existential quantifier | there exists an x belonging to A for which the proposition p(x) is true | The "∈A" can be dropped where A is clear from context. ∃! is used where only exactly one x exists for which p(x) is true. |
[edit] Sets
| Sign | Example | Meaning and verbal equivalent | Remarks |
|---|---|---|---|
| ∈ | x ∈ A | x belongs to A; x is an element of the set A | |
| ∉ | x ∉ A | x does not belongs to A; x is not an element of the set A | The negation stroke can also be vertical. |
| ∋ | A ∋ x | the set A contains x (as an element) | same meaning as x ∈ A |
| ∌ | A ∌ x | the set A does not contain x (as an element) | same meaning as x ∉ A |
| { } | {x1, x2, ..., xn} | set with elements x1, x2, ..., xn | also {xi : i ∈ I}, where I denotes a set of indices |
| { ∣ } | {x ∈ A ∣ p(x)} | set of those elements of A for which the proposition p(x) is true | Example: {x ∈ ℝ ∣ x > 5} The ∈A can be dropped where this set is clear from the context. |
| card | card(A) | number of elements in A; cardinal of A | |
| ∅ | the empty set | ||
| ℕ | the set of natural numbers; the set of positive integers and zero | ℕ = {0, 1, 2, 3, ...} Exclusion of zero is denoted by an asterisk: ℕ* = {1, 2, 3, ...} ℕk = {0, 1, 2, 3, ..., k − 1} |
|
| ℤ | the set of integers | ℤ = {..., −3, −2, −1, 0, 1, 2, 3, ...} ℤ* = ℤ \ {0} = {..., −3, −2, −1, 1, 2, 3, ...} |
|
| ℚ | the set of rational numbers | ℚ* = ℚ \ {0} | |
| ℝ | the set of real numbers | ℝ* = ℝ \ {0} | |
| ℂ | the set of complex numbers | ℂ* = ℂ \ {0} | |
| [,] | [a,b] | closed interval in ℝ from a (included) to b (included) | [a,b] = {x ∈ ℝ ∣ a ≤ x ≤ b} |
| ],] (,] |
]a,b] (a,b] |
left half-open interval in ℝ from a (excluded) to b (included) | ]a,b] = {x ∈ ℝ ∣ a < x ≤ b} |
| [,[ [,) |
[a,b[ [a,b) |
right half-open interval in ℝ from a (included) to b (excluded) | [a,b[ = {x ∈ ℝ ∣ a ≤ x < b} |
| ],[ (,) |
]a,b[ (a,b) |
open interval in ℝ from a (excluded) to b (excluded) | ]a,b[ = {x ∈ ℝ ∣ a < x < b} |
| ⊆ | B ⊆ A | B is included in A; B is a subset of A | Every element of B belongs to A. ⊂ is also used. |
| ⊂ | B ⊂ A | B is properly included in A; B is a proper subset of A | Every element of B belongs to A, but B is not equal to A. If ⊂ is used for "included", then ⊊ should be used for "properly included". |
| ⊈ | C ⊈ A | C is not included in A; C is not a subset of A | ⊄ is also used. |
| ⊇ | A ⊇ B | A includes B (as subset) | A contains every element of B. ⊃ is also used. B ⊆ A means the same as A ⊇ B. |
| ⊃ | A ⊃ B. | A includes B properly. | A contains every element of B, but A is not equal to B. If ⊃ is used for "includes", then ⊋ should be used for "includes properly". |
| ⊉ | A ⊉ C | A does not include C (as subset) | ⊅ is also used. A ⊉ C means the same as C ⊈ A. |
| ∪ | A ∪ B | union of A and B | The set of elements which belong to A or to B or to both A and B. A ∪ B = { x ∣ x ∈ A ∨ x ∈ B } |
| ⋃ |  |
union of a collection of sets |  , the set of elements belonging to at least one of the sets A1, …, An. , the set of elements belonging to at least one of the sets A1, …, An. 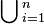 and and 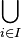 , ⋃i∈I are also used, where I denotes a set of indices. , ⋃i∈I are also used, where I denotes a set of indices. |
| ∩ | A ∩ B | intersection of A and B | The set of elements which belong to both A and B. A ∩ B = { x ∣ x ∈ A ∧ x ∈ B } |
| ⋂ |  |
intersection of a collection of sets |  , the set of elements belonging to all sets A1, …, An. , the set of elements belonging to all sets A1, …, An. 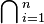 and and 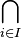 , ⋂i∈I are also used, where I denotes a set of indices. , ⋂i∈I are also used, where I denotes a set of indices. |
| \ | A \ B | difference between A and B; A minus B | The set of elements which belong to A but not to B. A \ B = { x ∣ x ∈ A ∧ x ∉ B } A − B should not be used. |
| ∁ | ∁AB | complement of subset B of A | The set of those elements of A which do not belong to the subset B. The symbol A is often omitted if the set A is clear from context. Also ∁AB = A \ B. |
| (,) | (a, b) | ordered pair a, b; couple a, b | (a, b) = (c, d) if and only if a = c and b = d. ⟨a, b⟩ is also used. |
| (,…,) | (a1, a2, …, an) | ordered n-tuple | ⟨a1, a2, …, an⟩ is also used. |
| × | A × B | cartesian product of A and B | The set of ordered pairs (a, b) such that a ∈ A and b ∈ B. A × B = { (a, b) ∣ a ∈ A ∧ b ∈ B } A × A × ⋯ × A is denoted by An, where n is the number of factors in the product. |
| Δ | ΔA | set of pairs (a, a) ∈ A × A where a ∈ A; diagonal of the set A × A | ΔA = { (a, a) ∣ a ∈ A } idA is also used. |
[edit] Miscellaneous signs and symbols
| Sign | Example | Meaning and verbal equivalent | Remarks | |
|---|---|---|---|---|
≝ |
a ≝ b | a is by definition equal to b[1] | := is also used | |
| = | a = b | a equals b | ≡ may be used to emphasize that a particular equality is an identity. | |
| ≠ | a ≠ b | a is not equal to b |  may be used to emphasize that a is not identically equal to b. may be used to emphasize that a is not identically equal to b. |
|
| ≙ | a ≙ b | a corresponds to b | On a 1:106 map: 1 cm ≙ 10 km. | |
| ≈ | a ≈ b | a is approximately equal to b | The symbol ≃ is reserved for "is asymptotically equal to". | |
| ∼ ∝ |
a ∼ b a ∝ b |
a is proportional to b | ||
| < | a < b | a is less than b | ||
| > | a > b | a is greater than b | ||
| ≤ | a ≤ b | a is less than or equal to b | The symbol ≦ is also used. | |
| ≥ | a ≥ b | a is greater than or equal to b | The symbol ≧ is also used. | |
| ≪ | a ≪ b | a is much less than b | ||
| ≫ | a ≫ b | a is much greater than b | ||
| ∞ | infinity | |||
| () [] {}  |
(a+b)c [a+b]c {a+b}c 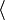 a+b a+b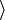 c c |
ac+bc, parentheses ac+bc, square brackets ac+bc, braces ac+bc, angle brackets |
In ordinary algebra, the sequence of (), [], {},  in order of nesting is not standardized. Special uses are made of (), [], {}, in order of nesting is not standardized. Special uses are made of (), [], {},  in particular fields.[2] in particular fields.[2] |
|
| ∥ | AB ∥ CD | the line AB is parallel to the line CD | ||
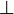 |
AB CD CD |
the line AB is perpendicular to the line CD[3] |
[edit] Operations
| Sign | Example | Meaning and verbal equivalent | Remarks |
|---|---|---|---|
| + | a + b | a plus b | |
| − | a − b | a minus b | |
| ± | a ± b | a plus or minus b | |
| ∓ | a ∓ b | a minus or plus b | −(a ± b) = −a ∓ b |
| ... | ... | ... | ... |
| ⋮ | |||
[edit] Functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| f | function f | ... |
| ... | ... | ... |
| ⋮ | ||
[edit] Exponential and logarithmic functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| ax | exponential function to the base a of x | ... |
| e | base of natural logarithms | e = 2.718 281 8... |
| ... | ... | ... |
| ⋮ | ||
[edit] Circular and hyperbolic functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| π | ratio of the circumference of a circle to its diameter | π = 3.141 592 6... |
| ... | ... | ... |
| ⋮ | ||
[edit] Complex numbers
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| i j | imaginary unit; i² = −1 | In electrotechnology, j is generally used. |
| Re z | real part of z | z = x + iy, where x = Re z and y = Im z |
| Im z | imaginary part of z | |
| ∣z∣ | absolute value of z; modulus of z | mod z is also used |
| arg z | argument of z; phase of z | z = reiφ, where r = ∣z∣ and φ = arg z, i.e. Re z = r cos φ and Im z = r sin φ |
| z* | (complex) conjugate of z | sometimes a bar above z is used instead of z* |
| sgn z | signum z | sgn z = z / ∣z∣ = exp(i arg z) for z ≠ 0, sgn 0 = 0 |
[edit] Matrices
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| A | matrix A | ... |
| ... | ... | ... |
| ⋮ | ||
[edit] Coordinate systems
| Coordinates | Position vector and its differential | Name of coordinate system | Remarks |
|---|---|---|---|
| x, y, z | ... | cartesian coordinates | ... |
| ρ, φ, z | ... | cylindrical coordinates | ... |
| r, θ, φ | ... | spherical coordinates | ... |
[edit] Vectors and tensors
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
a |
vector a | Instead of boldface, vectors can also be indicated by an arrow above the letter symbol. Any vector a can be multiplied by a number k, i.e. ka. |
| ... | ... | ... |
| ⋮ | ||
[edit] Special functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| Jl(x) | cylindrical Bessel functions (of the first kind) | ... |
| ... | ... | ... |
| ⋮ | ||
[edit] References and notes
- ^ a b Barry M. Taylor. Guide for the Use of the International System of Units (SI) ";Standardized mathematical signs; §10.1.2 p. 33: an abbreviated list of symbols from ISO 31-11". NIST. http://physics.nist.gov/cuu/pdf/sp811.pdf Guide for the Use of the International System of Units (SI).
- ^ These brace or fence characters are upper level unicode characters, fairly recently established and so may not display correctly in every browser. A close approximation of the appearance is found in the standard Latin characters: ( ), [ ], { }, < >. A more accurate glyph depiction of the mathematical angle bracket characters are found in the Chinese-Japanese-Korean (CJK) punctuation category: &x3008h; &x3009h;.
- ^ If the perpendicular symbol, ⟂, does not display correctly, it is similar to ⊥ (up tack: sometimes meaning orthogonal to) and it also appears similar to ⏊ (the dentistry: symbol light up and horizontal)

