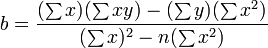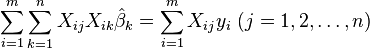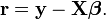Linear least squares

From Wikipedia, the free encyclopedia

The result of fitting a quadratic function $y=\beta_1+\beta_2x+\beta_3x^2\,$ (in blue) through a set of data points

(x i, y i)

(in red). In linear least squares the function need not be linear in the argument

x,

but only in the parameters

β j

that are determined to give the best fit.

Linear least squares is an important computational problem, that arises primarily in applications when it is desired to fit a linear mathematical model to measurements obtained from experiments. The goals of linear least squares are to extract predictions from the measurements and to reduce the effect of measurement errors. Mathematically, it can be stated as the problem of finding an approximate solution to an overdetermined system of linear equations. In statistics, it corresponds to the maximum likelihood estimate for a linear model with normally distributed error.

Linear least square problems admit a closed-form solution, in contrast to non-linear least squares problems, which often have to be solved by an iterative procedure.

1 Motivational example
- 1.1 Computation
2 The general problem
3 Uses in data fitting
4 Derivation of the normal equations
5 Computation
- 5.1 Inverting the normal equations
- 5.2 Orthogonal decomposition methods
6 Properties of the least-squares estimators
- 6.1 Limitations
7 Weighted linear least squares
8 Parameter errors, correlation and confidence limits
9 Residual values and correlation
10 Objective function
11 Typical uses and applications
12 Software for solving LLSP
13 Notes
14 References
15 External links

[edit] Motivational example

A plot of the data points (in red), the least squares line of best fit (in blue), and the residuals (in green).

As a result of an experiment, four $(x, y)$ data points were obtained, $(1,6),$ $(2,5),$ $(3,7),$ and $(4,10)$ (shown in red in the picture on the right). It is desired to find a line $y = β 1 + β 2 x$ that fits "best" these four points. In other words, we would like to find the numbers $β 1$ and $β 2$ that approximately solve the overdetermined linear system

$\begin{alignat}{3} \beta_1 + 1\beta_2 &&\; = \;&& 6 & \\ \beta_1 + 2\beta_2 &&\; = \;&& 5 & \\ \beta_1 + 3\beta_2 &&\; = \;&& 7 & \\ \beta_1 + 4\beta_2 &&\; = \;&& 10 & \\ \end{alignat}$

of four equations in two unknowns in some "best" sense.

The least squares approach to solving this problem is to try to make as small as possible the sum of squares of "errors" between the right- and left-hand sides of these equations, that is, to find the minimum of the function

$S(\beta_1, \beta_2)= \left[6-(\beta_1+1\beta_2)\right]^2 +\left[5-(\beta_1+2\beta_2) \right]^2 +\left[7-(\beta_1 + 3\beta_2)\right]^2 +\left[10-(\beta_1 + 4\beta_2)\right]^2.$

The minimum is determined by calculating the partial derivatives of $S (β 1,β 2)$ in respect to $β 1$ and $β 2$ and setting them to zero. This results in a system of two equations in two unknowns, called the normal equations, which, when solved, gives the solution

β 1 = 3.5

β 2 = 1.4

and the equation $y = 3.5 + 1.4 x$ of the line of best fit. The residuals, that is, the discrepancies between the $y$ values from the experiment and the $y$ values calculated using the line of best fit are then found to be $1.1,$ $- 1.3,$ $- 0.7,$ and $0.9$ (see the picture on the right). The minimum value of the sum of squares is $S (3.5,1.4) = 1.1 2 + ( - 1.3) 2 + ( - 0.7) 2 + 0.9 2 = 4.2.$

[edit] Computation

The common computational procedure to find a first-degree polynomial function approximation in a situation like this is as follows.

Use $n \$ for the number of data points.

Find the four sums: 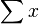$\sum x$ , $\sum x^2$ , $\sum y$ , and $\sum xy$ .

The calculations for the slope, m, and the y-intercept, b, are as follows.

$m= \frac{(\sum y)(\sum x)-n(\sum xy)}{( \sum x)^2 - n(\sum x^2)}$

and

$b=\frac {(\sum x)(\sum xy)-(\sum y)(\sum x^2)}{( \sum x)^2 - n(\sum x^2)}$

[edit] The general problem

Consider an overdetermined system

$\sum_{j=1}^{n} X_{ij}\beta_j = y_i,\ (i=1, 2, \dots, m),$

of $m$ linear equations in $n$ unknowns, $\beta_1, \beta_2, \dots, \beta_n,$ with $m > n,$ written in matrix form as

$\mathbf{X}\boldsymbol \beta = \mathbf y.$

Such a system usually has no solution, and the goal is then to find the numbers $β j$ which fit the equations "best", in the sense of solving the quadratic minimization problem

$\underset{\beta} \operatorname{arg\,min} \sum_{i=1}^{m}\left|y_i - \sum_{j=1}^{n} X_{ij}\beta_j\right|^2 .$

A justification for choosing this criterion is given in properties below. This minimization problem has a unique solution, provided that the $n$ columns of the matrix $X$ are linearly independent, given by solving the normal equations

$\mathbf{\left(X^TX\right)\hat \boldsymbol \beta=X^Ty}.$

[edit] Uses in data fitting

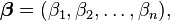The primary application of linear least squares is in data fitting. Given a set of m data points $y_1, y_2,\dots, y_m,$ consisting of experimentally measured values taken at m values $x_1, x_2,\dots, x_m$ of an independent variable ( $x i$ may be scalar or vector quantities), and given a model function $y=f(x, \boldsymbol \beta),$ with $\boldsymbol \beta = (\beta_1, \beta_2, \dots, \beta_n),$ it is desired to find the parameters $β j$ such that the model function fits "best" the data. In linear least squares, linearity is meant to be with respect to parameters $β j,$ so

$f(x, \boldsymbol \beta) = \sum_{j=1}^{n} \beta_j \phi_j(x).$

Here, the functions $φ j$ may be nonlinear with respect to the variable x.

Ideally, the model function fits the data exactly, so

$y_i = f(x_i, \boldsymbol \beta)$

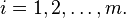for all $i=1, 2, \dots, m.$ This is usually not possible in practice, as there are more data points than there are parameters to be determined. The approach chosen then is to find the minimal possible value of the sum of squares of the residuals

$r_i(\boldsymbol \beta)= y_i - f(x_i, \boldsymbol \beta),\ (i=1, 2, \dots, m)$

so to minimize the function

$S(\boldsymbol \beta)=\sum_{i=1}^{m}r_i^2(\boldsymbol \beta).$

After substituting for $r i$ and then for $f$ , this minimization problem becomes the quadratic minimization problem above with $X i j = φ j (x i)$ , and the best fit can be found by solving the normal equations.

[edit] Derivation of the normal equations

S is minimized when its gradient with respect to each parameter is equal to zero. The elements of the gradient vector are the partial derivatives of S with respect to the parameters:

$\frac{\partial S}{\partial \beta_j}=2\sum_i r_i\frac{\partial r_i}{\partial \beta_j}=0 \ (j=1,2,\dots, n).$

Since $r_i= y_i - \sum_{j=1}^{n} X_{ij}\beta_j$ , the derivatives are

$\frac{\partial r_i}{\partial \beta_j}=-X_{ij}.$

Substitution of the expressions for the residuals and the derivatives into the gradient equations gives

$\frac{\partial S}{\partial \beta_j}=-2\sum_{i=1}^{m}X_{ij} \left( y_i-\sum_{k=1}^{n} X_{ik}\beta_k \right)=0.$

Upon rearrangement, the normal equations

$\sum_{i=1}^{m}\sum_{k=1}^{n} X_{ij}X_{ik}\hat \beta_k=\sum_{i=1}^{m} X_{ij}y_i\ (j=1,2,\dots, n)\,$

are obtained. The normal equations are written in matrix notation as

$\mathbf{\left(X^TX\right)\hat \boldsymbol \beta=X^Ty}.$

The solution of the normal equations yields the vector 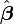$\hat \boldsymbol \beta$ of the optimal parameter values.

[edit] Computation

[edit] Inverting the normal equations

Although the algebraic solution of the normal equations can be written as

$\mathbf{ \hat \boldsymbol\beta=\left(X^TX \right)^{-1}X^Ty}$

it is not good practice to invert the normal equations matrix. An exception occurs in numerical smoothing and differentiation where an analytical expression is required.

If the matrix 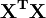$\mathbf{X^TX}$ is well-conditioned and positive definite, that is, it has full rank, the normal equations can be solved directly by using the Cholesky decomposition $\mathbf{X^TX=R^TR}$ , where R is an upper triangular matrix, giving

$\mathbf{ R^T R \hat \boldsymbol\beta = X^Ty}.$

The solution is obtained in two stages, a forward substitution, 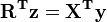$\mathbf{R^Tz=X^Ty}$ , followed by a backward substitution $\mathbf{R\hat \boldsymbol\beta=z}$ . Both subtitutions are facilitated by the triangular nature of R.

See example of linear regression for a worked-out numerical example with three parameters.

[edit] Orthogonal decomposition methods

Orthogonal decomposition methods of solving the least squares problem are slower than the normal equations method but are more numerically stable.

The extra stability results from not having to form the product 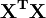$\mathbf{X^TX}$ . The residuals are written in matrix notation as

$\mathbf{r=y-X\boldsymbol\beta}.$

The matrix X is subjected to an orthogonal decomposition; the QR decomposition will serve to illustrate the process.

$\mathbf{X=QR}$

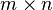where Q is an orthogonal $m \times m$ matrix and R is an $m \times n$ matrix which is partitioned into a 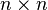$n \times n$ block, $\mathbf\R_n$ , and a $m-n \times n$ zero block. $\mathbf\R_n$ is upper triangular.

$\mathbf{R}= \begin{bmatrix} \mathbf{R}_n \\ \mathbf{0}\end{bmatrix}.$

The residual vector is left-multiplied by $\mathbf {Q^T}$ .

$\mathbf{Q^Tr=Q^T y -\left(Q^TQ\right)R \boldsymbol\beta}= \begin{bmatrix} \mathbf{\left(Q^T y\right)}_n -\mathbf{R}_n \boldsymbol\beta \\ \mathbf{\left(Q^T y \right)}_{m-n}\end{bmatrix} = \begin{bmatrix}\mathbf{U}\\\mathbf{L}\end{bmatrix}$

The sum of squares of the transformed residuals, $S=\mathbf{r^T Q Q^Tr}$ , is the same as before, $S=\mathbf{r^Tr}$ because Q is orthogonal.

$S=\mathbf{U^TU+L^TL}$

The minimum value of S is attained when the upper block, U, is zero. Therefore the parameters are found by solving

$\mathbf{R}_n \hat\boldsymbol\beta =\mathbf{\left(Q^T y \right)}_n.$

These equations are easily solved as $\mathbf{R}_n$ is upper triangular.

An alternative decomposition of X is the singular value decomposition (SVD)^[1]

$\mathbf{ X = U\Sigma V^*}.$

This is effectively another kind of orthogonal decomposition as both U and V are orthogonal. This method is the most computationally intensive, but is particularly useful if the normal equations matrix, 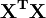$\mathbf{X^TX}$ , is very ill-conditioned (i.e. if its condition number multiplied by the machine's relative round-off error is appreciably large). In that case, including the smallest singular values in the inversion merely adds numerical noise to the solution. This can be cured using the truncated SVD approach, giving a more stable and exact answer, by explicitly setting to zero all singular values below a certain threshold and so ignoring them, a process closely related to factor analysis.

[edit] Properties of the least-squares estimators

The residual vector, $y-X\boldsymbol \hat \beta$ , which corresponds to the solution of a least squares system, $y=X\boldsymbol \beta +\epsilon$ , is orthogonal to the column space of the matrix

X

.

The gradient equations at the minimum can be written as

$\mathbf{(y-X\hat\boldsymbol\beta)X}=0.$

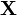A geometrical interpretation of these equations is that the vector of residuals, $\mathbf{y-X\hat\boldsymbol\beta}$ is orthogonal to the column space of $\mathbf{X}$ , since the dot product $\mathbf{(y-X\hat\boldsymbol\beta)\cdot Xv}$ is equal to zero for any conformal vector, $\mathbf{v}$ . This means that $\mathbf{y}-\mathbf{X}\boldsymbol \hat \beta$ is the shortest of all possible vectors $\mathbf{y}-\mathbf{X}\boldsymbol \beta$ , that is, the variance of the residuals is the minimum possible. This is illustrated at the right.

If the experimental errors, $\epsilon \,$ , are uncorrelated, have a mean of zero and a constant variance, $σ$ , the Gauss-Markov theorem states that the least-squares estimator, 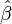$\hat \beta$ , has the minimum variance of all estimators that are linear combinations of the observations. In this sense it is the best, or optimal, estimator of the parameters. Note particularly that this property is independent of the statistical distribution function of the errors. In other words, the distribution function of the errors need not be a normal distribution. However, for some probability distributions, there is no guarantee that the least-squares solution is even possible given the observations; still, in such cases it is the best estimator that is both linear and unbiased.

For example, it is easy to show that the arithmetic mean of a set of measurements of a quantity is the least-squares estimator of the value of that quantity. If the conditions of the Gauss-Markov theorem apply, the arithmetic mean is optimal, whatever the distribution of errors of the measurements might be.

However, in the case that the experimental errors do belong to a Normal distribution, the least-squares estimator is also a maximum likelihood estimator.^[2]

These properties underpin the use of the method of least squares for all types of data fitting, even when the assumptions are not strictly valid.

[edit] Limitations

An assumption underlying the treatment given above is that the independent variable, x, is free of error. In practice, the errors on the measurements of the independent variable are usually much smaller than the errors on the dependent variable and can therefore be ignored. When this is not the case, total least squares also known as Errors-in-variables model, or Rigorous least squares, should be used. This can be done by adjusting the weighting scheme to take into account errors on both the dependent and independent variables and then following the standard procedure.^[3]^[4]

In some cases the (weighted) normal equations matrix 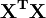$\mathbf{X^TX}$ is ill-conditioned; this occurs when the measurements have only a marginal effect on one or more of the estimated parameters.^[5] In these cases, the least squares estimate amplifies the measurement noise and may be grossly inaccurate. Various regularization techniques can be applied in such cases, the most common of which is called Tikhonov regularization. If further information about the parameters is known, for example, a range of possible values of x, then minimax techniques can also be used to increase the stability of the solution.

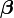Another drawback of the least squares estimator is the fact that the norm of the residuals, $\|\mathbf{y-X\boldsymbol\beta}\|$ is minimized, whereas in some cases one is truly interested in obtaining small error in the parameter $\mathbf{\boldsymbol\beta}$ , e.g., a small value of $\|\boldsymbol\beta-\hat\boldsymbol\beta\|$ . However, since $\boldsymbol\beta$ is unknown, this quantity cannot be directly minimized. If a prior probability on 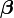$\boldsymbol\beta$ is known, then a Bayes estimator can be used to minimize the mean squared error, $E \left\{ \| \boldsymbol\beta - \hat\boldsymbol\beta \|^2 \right\}$ . The least squares method is often applied when no prior is known. Surprisingly, however, better estimators can be constructed, an effect known as Stein's phenomenon. For example, if the measurement error is Gaussian, several estimators are known which dominate, or outperform, the least squares technique; the best known of these is the James-Stein estimator.

[edit] Weighted linear least squares

When the observations are not equally reliable, a weighted sum of squares

$S=\sum_{i=1}^{m}W_{ii}r_i^2$

may be minimized.

Each element of the diagonal weight matrix, W should,ideally, be equal to the reciprocal of the variance of the measurement.^[6] The normal equations are then

$\mathbf{\left(X^TWX\right)\hat \boldsymbol \beta=X^TWy}.$

[edit] Parameter errors, correlation and confidence limits

The parameter values are linear combinations of the observed values

$\mathbf{\hat \beta=(X^TWX)^{-1}X^TWy}.$

Therefore an expression for the errors on the parameter can be obtained by error propagation from the errors on the observations. Let the variance-covariance matrix for the observations be denoted by M and that of the parameters by M^$β$. Then,

$\mathbf{M^\beta=(X^TWX)^{-1}X^TW M W^TX(X^TWX)^{-1}}.$

When $\mathbf{W=M^{-1}}$ , this simplifies to

$\mathbf{M^\beta=(X^TWX)^{-1}}.$

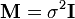When unit weights are used ( $\mathbf{W=I, \hat \beta=(X^TX)^{-1}X^Ty}$ ) it is implied that the experimental errors are uncorrelated and all equal: $\mathbf{M}=\sigma^2 \mathbf{I}$ , where $\sigma^2\,$ is known as the variance of an observation of unit weight, and $\mathbf{I}$ is an identity matrix. In this case $\sigma^2\,$ is approximated by $\frac{S}{n-m}$ , where S is the minimum value of the objective function

$\mathbf{M^\beta=}\frac{S}{n-m}\mathbf{(X^TX)^{-1}}.$

In all cases, the variance of the parameter $β i$ is given by $M^\beta_{ii}$ and the covariance between parameters $β i$ and $β j$ is given by $M^\beta_{ij}$ . Standard deviation is the square root of variance and the correlation coefficient is given by $\rho_{ij} = M^\beta_{ij}/\sigma_i/\sigma_j$ . These error estimates reflect only random errors in the measurements. The true uncertainty in the parameters is larger due to the presence of systematic errors which, by definition, cannot be quantified. Note that even though the observations may be un-correlated, the parameters are always correlated.

It is often assumed, for want of any concrete evidence, that the error on a parameter belongs to a Normal distribution with a mean of zero and standard deviation $σ$ . Under that assumption the following confidence limits can be derived.

68% confidence limits, $\hat \beta \pm \sigma$

95% confidence limits, $\hat \beta \pm 2\sigma$

99% confidence limits, $\hat \beta \pm 2.5\sigma$

The assumption is not unreasonable when m>>n. If the experimental errors are normally distributed the parameters will belong to a Student's t-distribution with m-n degrees of freedom. When m>>n Student's t-distribution approximates to a Normal distribution. Note, however, that these confidence limits cannot take systematic error into account. Also, parameter errors should be quoted to one significant figure only, as they are subject to sampling error.^[7]

When the number of observations is relatively small, Chebychev's inequality can be used for an upper bound on probabilities, regardless of any assumptions about the distribution of experimental errors: the maximum probabilities that a parameter will be more than 1, 2 or 3 standard deviations away from its expectation value are 100%, 25% and 11% respectively.

[edit] Residual values and correlation

The residuals are related to the observations by

$\mathbf{\hat r=y-X \hat \beta=y-X \left(X^TWX \right)^{-1}X^T W y}$

The symmetric, idempotent matrix $\mathbf{X \left(X^TWX \right)^{-1}X^T W}$ is known in the statistics literature as the hat matrix, $\mathbf{H}$ . ( $\mathbf{H}$ is idempotent because it is a projection.) Thus,

$\mathbf{\hat r=\left(I-H \right) y}$

where I is an identity matrix. The variance-covariance matrice of the residuals, M^r is given by

$\mathbf{M^r=\left(I-H \right) M \left(I-H \right)}.$

This shows that even though the observations may be uncorrelated, the residuals are always correlated.

The sum of residual values is equal to zero whenever the model function contains a constant term. Left-multiply the expression for the residuals by 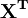$\mathbf{X^T}$ .

$\mathbf{X^T\hat r=X^Ty-X^TX\boldsymbol\hat\beta=X^Ty-(X^TX)(X^TX)^{-1}X^Ty=0}$

Say, for example, that the first term of the model is a constant, so that $X i 1 = 1$ for all i. In that case it follows that

$\sum_i^m X_{i1} \hat r_i=\sum_i^m \hat r_i=0.$

Thus, in the motivational example, above, the fact that the sum of residual values is equal to zero it is not accidental but is a consequence of the presence of the constant term, α, in the model.

If experimental error follows a normal distribution, then, because of the linear relationship between residuals and observations, so should residuals,^[8] but since the observations are only a sample of the population of all possible observations, the residuals should belong to a Student's t-distribution. Studentized residuals are useful in making a statistical test for an outlier when a particular residual appears to be excessively large.

[edit] Objective function

The objective function can be written as

$S=\mathbf{ y^T(I-H)^T(I-H)y=y^T(I-H)y}$

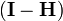since $\mathbf{ (I-H)}$ is also symmetric and idempotent. It can be shown from this,^[9] that the expected value of S is m-n. Note, however, that this is true only if the weights have been assigned correctly. If unit weights are assumed, the expected value of S is $(m - n)σ 2$ , where $σ 2$ is the variance of an observation.

If it is assumed that the residuals belong to a Normal distribution, the objective function, being a sum of weighted squared residuals, will belong to a Chi-square ( $χ 2$ ) distribution with m-n degrees of freedom. Some illustrative percentile values of $χ 2$ are given in the following table.^[10]

m-n	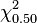$\chi ^2 _{0.50}$	$\chi ^2 _{0.95}$	$\chi ^2 _{0.99}$
10	9.34	18.3	23.2
25	24.3	37.7	44.3
100	99.3	124	136

These values can be used for a statistical criterion as to the goodness-of-fit. When unit weights are used, the numbers should be divided by the variance of an observation.

[edit] Typical uses and applications

Polynomial fitting: models are polynomials in an independent variable, x:
- Straight line: $f(x, \boldsymbol \beta)=\beta_1 +\beta_2 x$ .^[11]
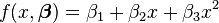- Quadratic: $f(x, \boldsymbol \beta)=\beta_1 + \beta_2 x +\beta_3 x^2$ .
- Cubic, quartic and higher polynomials. For high-order polynomials the use of orthogonal polynomials is recommended.^[5]^[12]
Numerical smoothing and differentiation — this is an application of polynomial fitting.
Multinomials in more than one independent variable, including surface fitting
Curve fitting with B-splines ^[3]
Chemometrics, Calibration curve, Standard addition, Gran plot, analysis of mixtures

[edit] Software for solving LLSP

1. Free and opensource, with OSI-Approved licenses

Name	License	Brief info
bvls	BSD	Fortran code by Robert L. Parker & Philip B. Stark
lapack dgelss	BSD	made by Univ. of Tennessee, Univ. of California Berkeley, NAG Ltd., Courant Institute, Argonne National Lab, and Rice University
OpenOpt	BSD	universal cross-platform Python-written numerical optimization framework; see its LLSP page and full list of problems

2. Commercial

MATLAB lsqlin

[edit] Notes

^ Lawson, C. L.; Hanson, R. J. (1974). Solving Least Squares Problems. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0138225850.
^ Margenau, Henry; Murphy, George Moseley (1956). The Mathematics of Physics and Chemistry. Princeton: Van Nostrand.
^ ^a ^b Gans, Peter (1992). Data fitting in the Chemical Sciences. New York: Wiley. ISBN 0471934127.
^ Deming, W. E. (1943). Statistical adjustment of Data. New York: Wiley.
^ ^a ^b When fitting polynomials the normal equations matrix is a Vandermonde matrix. Vandermode matrices become increasingly ill-conditioned as the order of the matrix increases.
^ This implies that the observations are uncorrelated. If the observations are correlated, the expression $\textstyle S=\sum_k \sum_j r_k W_{kj} r_j\,$ applies. In this case the weight matrix should ideally be equal to the inverse of the variance-covariance matrix of the observations.
^ Mandel, John (1964). The Statistical Analysis of Experimental Data. New York: Interscience.
^ Mardia, K. V.; Kent, J. T.; Bibby, J. M. (1979). Multivariate analysis. New York: Academic Press. ISBN 0124712509.
^ Hamilton, W. C. (1964). Statistics in Physical Science. New York: Ronald Press.
^ Spiegel, Murray R. (1975). Schaum's outline of theory and problems of probability and statistics. New York: McGraw-Hill. ISBN 0585267391.
^ Acton, F. S. (1959). Analysis of Straight-Line Data. New York: Wiley.
^ Guest, P. G. (1961). Numerical Methods of Curve Fitting. Cambridge: Cambridge University Press.

[edit] References

Björck, Åke (1996). Numerical methods for least squares problems. Philadelphia: SIAM. ISBN 0-89871-360-9.
Bevington, Philip R; Robinson, Keith D (2003). Data Reduction and Error Analysis for the Physical Sciences. McGraw Hill. ISBN 0072472278.

[edit] External links

Theory

Online utilities

Online Linear Least Squares Utility

[0] Lawson, C. L.; Hanson, R. J. (1974). Solving Least Squares Problems. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0138225850.

[1] Margenau, Henry; Murphy, George Moseley (1956). The Mathematics of Physics and Chemistry. Princeton: Van Nostrand.

[pg-2] Gans, Peter (1992). Data fitting in the Chemical Sciences. New York: Wiley. ISBN 0471934127.

[3] Deming, W. E. (1943). Statistical adjustment of Data. New York: Wiley.

[vm-4] When fitting polynomials the normal equations matrix is a Vandermonde matrix. Vandermode matrices become increasingly ill-conditioned as the order of the matrix increases.

[5] This implies that the observations are uncorrelated. If the observations are correlated, the expression $\textstyle S=\sum_k \sum_j r_k W_{kj} r_j\,$ applies. In this case the weight matrix should ideally be equal to the inverse of the variance-covariance matrix of the observations.

[6] Mandel, John (1964). The Statistical Analysis of Experimental Data. New York: Interscience.

[7] Mardia, K. V.; Kent, J. T.; Bibby, J. M. (1979). Multivariate analysis. New York: Academic Press. ISBN 0124712509.

[8] Hamilton, W. C. (1964). Statistics in Physical Science. New York: Ronald Press.

[9] Spiegel, Murray R. (1975). Schaum's outline of theory and problems of probability and statistics. New York: McGraw-Hill. ISBN 0585267391.

[10] Acton, F. S. (1959). Analysis of Straight-Line Data. New York: Wiley.

[11] Guest, P. G. (1961). Numerical Methods of Curve Fitting. Cambridge: Cambridge University Press.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Linear least squares

From Wikipedia, the free encyclopedia

Contents

[edit] Motivational example

[edit] Computation

[edit] The general problem

[edit] Uses in data fitting

[edit] Derivation of the normal equations

[edit] Computation

[edit] Inverting the normal equations

[edit] Orthogonal decomposition methods

[edit] Properties of the least-squares estimators

[edit] Limitations

[edit] Weighted linear least squares

[edit] Parameter errors, correlation and confidence limits

[edit] Residual values and correlation

[edit] Objective function

[edit] Typical uses and applications

[edit] Software for solving LLSP

[edit] Notes

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages