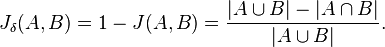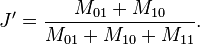algorithm analysis attributes bachelorarbeit binary classifier clustering coefficient collectiveintelligence community computerscience cosine-similarity cs datamining del.icio.us dissimilarity distance distance-metric jaccard math nlp phd programming research science sets similarity statistics tanimoto

My tags:

From Wikipedia, the free encyclopedia

The Jaccard index, also known as the Jaccard similarity coefficient (originally coined coefficient de communauté by Paul Jaccard), is a statistic used for comparing the similarity and diversity of sample sets.

The Jaccard coefficient measures similarity between sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets:

The Jaccard distance, which measures dissimilarity between sample sets, is complementary to the Jaccard coefficient and is obtained by subtracting the Jaccard coefficient from 1, or, equivalently, by dividing the difference of the sizes of the union and the intersection of two sets by the size of the union:

Contents 1 Similarity of asymmetric binary attributes 2 Tanimoto coefficient (extended Jaccard coefficient) 3 See also 4 References 5 External links

[edit] Similarity of asymmetric binary attributes

Given two objects, A and B, each with n binary attributes, the Jaccard coefficient is a useful measure of the overlap that A and B share with their attributes. Each attribute of A and B can either be 0 or 1. The total number of each combination of attributes for both A and B are specified as follows:

M₁₁ represents the total number of attributes where A and B both have a value of 1.

M₀₁ represents the total number of attributes where the attribute of A is 0 and the attribute of B is 1.

M₁₀ represents the total number of attributes where the attribute of A is 1 and the attribute of B is 0.

M₀₀ represents the total number of attributes where A and B both have a value of 0.

Each attribute must fall into one of these four categories, meaning that

M₁₁ + M₀₁ + M₁₀ + M₀₀ = n.

The Jaccard similarity coefficient, J, is given as

The Jaccard distance, J', is given as

[edit] Tanimoto coefficient (extended Jaccard coefficient)

Cosine similarity is a measure of similarity between two vectors of n dimensions by finding the angle between them, often used to compare documents in text mining. Given two vectors of attributes, A and B, the cosine similarity, θ, is represented using a dot product and magnitude as

For text matching, the attribute vectors A and B are usually the tf-idf vectors of the documents.

Since the angle, θ, is in the range of [0,π], the resulting similarity will yield the value of π as meaning exactly opposite, π / 2 meaning independent, 0 meaning exactly the same, with in-between values indicating intermediate similarities or dissimilarities.

This cosine similarity metric may be extended such that it yields the Jaccard coefficient in the case of binary attributes. This is the Tanimoto coefficient, T(A,B), represented as

[edit] See also

• Sørensen's quotient of similarity
• Mountford's index of similarity
• Hamming distance
• Correlation
• Dice's coefficient

[edit] References

• Pang-Ning Tan, Michael Steinbach and Vipin Kumar, Introduction to Data Mining (2005), ISBN 0-321-32136-7
• Paul Jaccard (1901) Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bulletin del la Société Vaudoise des Sciences Naturelles 37, 547-579.
• Tanimoto, T.T. (1957) IBM Internal Report 17th Nov. 1957.

[edit] External links

• Jaccard's index and species diversity
• Example of Jaccard's coefficient
• Introduction to Data Mining lecture notes from Tan, Steinbach, Kumar
• http://sourceforge.net/projects/simmetrics/ SimMetrics a sourceforge implementation of this and many other similarity metrics