Minimum spanning tree
From Wikipedia, the free encyclopedia
| This article is missing citations or needs footnotes. Please help add inline citations to guard against copyright violations and factual inaccuracies. (February 2009) |
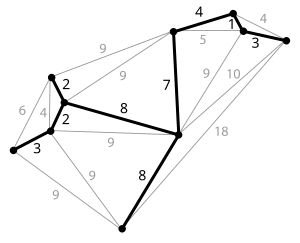
Given a connected, undirected graph, a spanning tree of that graph is a subgraph which is a tree and connects all the vertices together. A single graph can have many different spanning trees. We can also assign a weight to each edge, which is a number representing how unfavorable it is, and use this to assign a weight to a spanning tree by computing the sum of the weights of the edges in that spanning tree. A minimum spanning tree (MST) or minimum weight spanning tree is then a spanning tree with weight less than or equal to the weight of every other spanning tree. More generally, any undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of minimum spanning trees for its connected components.
One example would be a cable TV company laying cable to a new neighborhood. If it is constrained to bury the cable only along certain paths, then there would be a graph representing which points are connected by those paths. Some of those paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house. There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost.
Contents |
[edit] Properties
[edit] Possible multiplicity
There may be several minimum spanning trees of the same weight; in particular, if all weights are the same, every spanning tree is minimum.
[edit] Uniqueness
If each edge has a distinct weight then there will only be one, unique minimum spanning tree. This can be proved by induction or contradiction. This is true in many realistic situations, such as the cable TV company example above, where it's unlikely any two paths have exactly the same cost. This generalizes to spanning forests as well.
A proof of uniqueness by contradiction is as follows. Say we have an algorithm that finds an MST (which we will call A) based on the structure of the graph and the order of the edges when ordered by weight. (Such algorithms do exist, see below.) Assume for the moment that this MST is not unique and that there is another spanning tree, B, with equal weight. If there are n vertices in the graph, then each tree has n-1 edges. There are some edges which belong to B but not to A. What happens if we decrease the weight of one of these edges by a tiny amount ε so that we do not change the overall ordering of all the edges of the graph when ordered by weight? (This is possible because all weights are separated by positve amounts.) It will not change the result of our algorithm, which still gives tree A. But tree B will now have a weight ε less than what it had before, which means that A is not minimal, contrary to assumption. Because of this contradiction, we conclude that the assumption that there can be a second MST was false.
[edit] Minimum-cost subgraph
If the weights are non-negative, then a minimum spanning tree is in fact the minimum-cost subgraph connecting all vertices, since subgraphs containing cycles necessarily have more total weight.
[edit] Cycle property
For any cycle C in the graph, if the weight of an edge e of C is larger than the weights of other edges of C, then this edge cannot belong to an MST. Assuming the contrary, i.e. that e belongs to an MST T1, then deleting e will break T1 into two subtrees with the two ends of e in different subtrees. The remainder of C reconnects the subtrees, hence there is an edge f of C with ends in different subtrees, i.e., it reconnects the subtrees into a tree T2 with weight less than that of T1, because the weight of f is less than the weight of e.
[edit] Cut property
For any cut C in the graph, if the weight of an edge e of C is smaller than the weights of other edges of C, then this edge belongs to all MSTs of the graph. Indeed, assume the contrary, i.e., e does not belong to an MST T1. then adding e to T1 will produce a cycle, which must have another edge e2 from T1 in the cut C. Replacing e2 with e would produce a tree T1 of smaller weight.
[edit] Pseudocode
In the most general case, a greedy algorithm for computing an MST has the following form:
function MST(G,W):
T = {}
while T does not form a spanning tree:
find an edge in E that is safe for T
T = T union {(u,v)}
return T
where "safe" means that it forms an MST.
[edit] Algorithms
The first algorithm for finding a minimum spanning tree was developed by Czech scientist Otakar Borůvka in 1926 (see Borůvka's algorithm). Its purpose was an efficient electrical coverage of Moravia. There are now two algorithms commonly used, Prim's algorithm and Kruskal's algorithm. All three are greedy algorithms that run in polynomial time, so the problem of finding such trees is in FP, and related decision problems such as determining whether a particular edge is in the MST or determining if the minimum total weight exceeds a certain value are in P. Another greedy algorithm not as commonly used is the reverse-delete algorithm, which is the reverse of Kruskal's algorithm.
The fastest minimum spanning tree algorithm to date was developed by Bernard Chazelle, which is based on the Soft Heap, an approximate priority queue. [1] [2] Its running time is O(e α(e,v)), where e is the number of edges, v is the number of vertices and α is the classical functional inverse of the Ackermann function. The function α grows extremely slowly, so that for all practical purposes it may be considered a constant no greater than 4; thus Chazelle's algorithm takes very close to linear time.
What is the fastest possible algorithm for this problem? That is one of the oldest open questions in computer science. There is clearly a linear lower bound, since we must at least examine all the weights. If the edge weights are integers with a bounded bit length, then deterministic algorithms are known with linear running time. [3] For general weights, there are randomized algorithms whose expected running time is linear. [4] [5]
Whether there exists a deterministic algorithm with linear running time for general weights is still an open question. However, Seth Pettie and Vijaya Ramachandran have found a provably optimal deterministic minimum spanning tree algorithm, the computational complexity of which is unknown. [6]
More recently, research has focused on solving the minimum spanning tree problem in a highly parallelized manner. With a linear number of processors it is possible to solve the problem in O(logn) time. [7] [8]. A 2003 paper "Fast Shared-Memory Algorithms for Computing the Minimum Spanning Forest of Sparse Graphs" by David A. Bader and Guojing Cong demonstrates a pragmatic algorithm that can compute MSTs 5 times faster on 8 processors than an optimized sequential algorithm.[9] Typically, parallel algorithms are based on Boruvka's algorithm—Prim's and especially Kruskal's algorithm do not scale as well to additional processors.
Other specialized algorithms have been designed for computing minimum spanning trees of a graph so large that most of it must be stored on disk at all times. These external storage algorithms, for example as described in "Engineering an External Memory Minimum Spanning Tree Algorithm" by Roman Dementiev et al.,[10] can operate as little as 2 to 5 times slower than a traditional in-memory algorithm; they claim that "massive minimum spanning tree problems filling several hard disks can be solved overnight on a PC." They rely on efficient external storage sorting algorithms and on graph contraction techniques for reducing the graph's size efficiently.
The problem can also be approached in a distributed manner. If each node is considered a computer and no node knows anything except its own connected links, one can still calculate the distributed minimum spanning tree.
[edit] MST on complete graphs
Alan M. Frieze showed that given a complete graph on n vertices, with edge weights that are independent identically distributed random variables with distribution function F satisfying F'(0) > 0, then as n approaches infinity the expected weight of the MST approaches ζ(3) / F'(0), where ζ is the Riemann zeta function. Under the additional assumption of finite variance, Alan M. Frieze also proved convergence in probability. Subsequently, J. Michael Steele showed that the variance assumption could be dropped.
In later work, Svante Janson proved a central limit theorem for weight of the MST.
For uniform random weights in [0,1], the exact expected size of the minimum spanning tree has been computed for small complete graphs.
| Vertices | Expected size | Approximative expected size |
|---|---|---|
| 2 | 1 / 2 | 0.5 |
| 3 | 3 / 4 | 0.75 |
| 4 | 31 / 35 | 0.8857143 |
| 5 | 893 / 924 | 0.9664502 |
| 6 | 278 / 273 | 1.0183151 |
| 7 | 30739 / 29172 | 1.053716 |
| 8 | 199462271 / 184848378 | 1.0790588 |
| 9 | 126510063932 / 115228853025 | 1.0979027 |
[edit] Related problems
A related graph is the k-minimum spanning tree (k-MST) which is the tree that spans some subset of k vertices in the graph with minimum weight.
A set of k-smallest spanning trees is a subset of k spanning trees (out of all possible spanning trees) such that no spanning tree outside the subset has smaller weight. [11] (Note that this problem is unrelated to the k-minimum spanning tree.)
The Euclidean minimum spanning tree is a spanning tree of a graph with edge weights corresponding to the Euclidean distance between vertices.
In the distributed model, where each node is considered a computer and no node knows anything except its own connected links, one can consider Distributed minimum spanning tree. Mathematical definition of the problem is the same but has different approaches for solution.
For directed graphs, the minimum spanning tree problem can be solved in quadratic time using the Chu–Liu/Edmonds algorithm.
[edit] See also
- Reverse-Delete algorithm
- Dijkstra's algorithm
- Spanning tree protocol, used in switched networks
- Edmonds's algorithm
- Borůvka's algorithm
- Kruskal's algorithm
- Prim's algorithm
- Distributed minimum spanning tree
[edit] References
- Otakar Boruvka on Minimum Spanning Tree Problem (translation of the both 1926 papers, comments, history) (2000) Jaroslav Nesetril, Eva Milková, Helena Nesetrilová (section 7 gives his algorithm, which looks like a cross between Prim's and Kruskal's)
- Bernard Chazelle. A Minimum Spanning Tree Algorithm with Inverse-Ackermann Type Complexity. JACM 47(6):1028–1047, 2000.
- Bernard Chazelle. The Soft Heap: An Approximate Priority Queue with Optimal Error Rate. JACM 47(6):1012–1027, 2000.
- David Karger, Philip Klein, and Robert Tarjan. A Randomized Linear Time Algorithm to Find Minimum Spanning Trees. JACM 42(2):321–328, 1995.
- Seth Pettie and Vijaya Ramachandran. An Optimal Minimum Spanning Tree Algorithm. JACM 49(1):16–34, 2002.
- K. W. Chong, Y. Han, and T. W. Lam Concurrent Threads and Optimal Minimum Spanning Trees Algorithm. JACM 48(1)297–323, 2001.
- Seth Pettie and Vijaya Ramachandran. A Randomized Time-Work Optimal Algorithm to Find a Minimum Spanning Forest. SIAM J. Comput. 31(6):1879–1895, 2002.
- Michael Fredman and Dan Willard. Trans-dichotomous Algorithms for Minimum Spanning Trees and Shortest Paths. J. Comput. Syst. Sci. 48(3):533–551, 1994.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 23: Minimum Spanning Trees, pp.561–579.
- Two Algorithms for Generating Weighted Spanning Trees in Order, Harold Gabow, 1977
- State-of-the-Art Algorithms for Minimum Spanning Trees: A Tutorial Discussion, Jason Eisner, 1997

