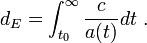Event horizon
From Wikipedia, the free encyclopedia
| General relativity | ||||||||||||
 |
||||||||||||
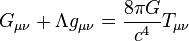| Einstein field equations | ||||||||||||
| Introduction to... Mathematical formulation of... Resources
|
||||||||||||
 |
This article includes a list of references or external links, but its sources remain unclear because it has insufficient inline citations. Please help to improve this article by introducing more precise citations where appropriate. (March 2009) |
In general relativity, an event horizon is a boundary in spacetime, most often an area surrounding a black hole, beyond which events cannot affect an outside observer. Light emitted from beyond the horizon can never reach the observer, and anything that passes through the horizon from the observer's side appears to freeze in place, with its image becoming more redshifted as time proceeds.
More specific types of horizon include the related but distinct absolute and apparent horizons found around a black hole. Still other distinct notions include the Cauchy and Killing horizon; the photon spheres and ergospheres of the Reissner-Nordström solution; particle and cosmological horizons relevant to cosmology; and isolated and dynamical horizons important in current black hole research.
Contents |
[edit] Event horizon of a black hole
The most commonly known example of an event horizon is defined around general relativity's description of a black hole, a celestial object so dense that no matter or radiation can escape its gravitational field. This is sometimes described as the boundary within which the black hole's escape velocity is greater than the speed of light. An alternate description is that within this horizon, all lightlike paths (paths that light could take), and hence all paths in the forward light cones of particles within the horizon, are warped so as to fall farther into the hole. Once a particle is inside the horizon, moving into the hole is as inevitable as moving forward in time (and can actually be thought of as equivalent to doing so, depending on the spacetime coordinate system used).
The surface at the Schwarzschild radius acts as an event horizon in a non-rotating body that fits inside this radius. (A rotating black hole operates slightly differently.) The Schwarzschild radius of an object is proportional to the mass. For the mass of the Sun it is approximately 3 km, and for that of the Earth about 9 mm. For a black hole created by the collapse of a star (which has a mass above the Chandrasekhar limit) the lower limit is about 4 km.
Black hole event horizons are especially noteworthy for three reasons. First, there are many examples near enough to study. Second, black holes tend to pull in matter from their environment, which provides examples where matter about to pass through an event horizon is expected to be observable. Third, the description of black holes given by general relativity is known to be an approximation, and it is expected that quantum gravity effects become significant near the vicinity of the event horizon. This allows observations of matter in the vicinity of a black hole's event horizon to be used to indirectly study general relativity and proposed extensions to it.
The definition of "event horizon" given by Hawking & Ellis,[1] Misner, Thorne & Wheeler,[2] and Wald[3] differs from the one presented here. Their definition rules out the cosmological and particle horizons presented below (as well as the apparent horizon). However, modern usage has brought those ideas under the umbrella of the term "event horizon".[4] To make the distinction clearer, some authors refer to their more specific notion of a horizon as an "absolute horizon". In the context of black holes, event horizon almost always refers to the absolute horizon, as distinct from the apparent horizon.
[edit] Event horizon of the observable universe
The particle horizon of the observable universe is the boundary that represents the maximum distance at which events can currently be observed. For events beyond that distance, light hasn't had time to reach our location, even if it were emitted at the time the universe began. How the particle horizon changes with time depends on the nature of the expansion of the universe. If the expansion has certain characteristics, there are parts of the universe that will never be observable, no matter how long the observer waits for light from those regions to arrive. The boundary past which events can't ever be observed is an event horizon, and it represents the maximum extent of the particle horizon.
The criterion for determining whether an event horizon for the universe exists is as follows. Define a comoving distance dE by
In this equation, a is the scale factor, c is the speed of light, and t0 is the age of the universe. If 
, (i.e. points arbitrarily as far away as can be observed), then no event horizon exists. If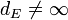 
, a horizon is present.
Examples of cosmological models without an event horizon are universes dominated by matter or by radiation. An example of a cosmological model with an event horizon is a universe dominated by the cosmological constant (a de Sitter universe).
[edit] Event horizon of an accelerated particle
If a particle is moving at a constant velocity in a non-expanding universe free of gravitational fields, any event that occurs in that universe will eventually be observable by the particle, because the forward light cones from these events intersect the particle's world line. On the other hand, if the particle is accelerating, in some situations light cones from some events never intersect the particle's world line. Under these conditions, an event horizon is present in the particle's (accelerating) reference frame, representing a boundary beyond which events are unobservable.
For example, this occurs with a uniformly accelerated particle. A spacetime diagram of this situation is shown in the figure to the right. As the particle accelerates, it approaches, but never reaches, the speed of light with respect to its original reference frame. On the spacetime diagram, its path is a hyperbola, which asymptotically approaches a 45 degree line (the path of a light ray). An event whose light cone's edge is this asymptote or is farther away than this asymptote can never be observed by the accelerating particle. In the particle's reference frame, there appears to be a boundary behind it from which no signals can escape (an event horizon).
While approximations of this type of situation can occur in the real world[citation needed] (in particle accelerators, for example), a true event horizon is never present, as the particle must be accelerated indefinitely (requiring arbitrarily large amounts of energy and an arbitrarily large apparatus).
[edit] Interacting with an event horizon
A misconception concerning event horizons, especially black hole event horizons, is that they represent an immutable surface that destroys objects that approach them. In practice, all event horizons appear to be some distance away from any observer, and objects sent towards an event horizon never appear to cross it from the sending observer's point of view (as the horizon-crossing event's light cone never intersects the observer's world line). Attempting to make an object approaching the horizon remain stationary with respect to an observer requires applying a force whose magnitude becomes unbounded (becoming infinite) the closer it gets.
For the case of a horizon perceived by a uniformly accelerating observer in empty space, the horizon seems to remain a fixed distance from the observer no matter how its surroundings move. Varying the observer's acceleration may cause the horizon to appear to move over time, or may prevent an event horizon from existing, depending on the acceleration function chosen. The observer never touches the horizon, and never passes a location where it appeared to be.
For the case of a horizon perceived by an occupant of a De Sitter Universe, the horizon always appears to be a fixed distance away for a non-accelerating observer. It is never contacted, even by an accelerating observer.
For the case of the horizon around a black hole, observers stationary with respect to a distant object will all agree on where the horizon is. While this seems to allow an observer lowered towards the hole on a rope to contact the horizon, in practice this cannot be done. If the observer is lowered very slowly, then, in the observer's frame of reference, the horizon appears to be very far away, and ever more rope needs to be paid out to reach the horizon. If the observer is quickly lowered by another observer, then indeed the first observer, and some of the rope can touch and even cross the (second observer's) event horizon. If the rope is pulled taut to fish the first observer back out, then the forces along the rope increase without bound as they approach the event horizon, and at some point the rope must break. Furthermore, the break must occur not at the event horizon, but at a point where the second observer can observe it.
Attempting to stick a rigid rod through the hole's horizon cannot be done: if the rod is lowered extremely slowly, then it is always too short to touch the event horizon, as the coordinate frames near the tip of the rod are extremely compressed. From the point of view of an observer at the end of the rod, the event horizon remains hopelessly out of reach. If the rod is lowered quickly, then the same problems as with the rope are encountered: the rod must break and the broken-off pieces inevitably fall in.
These peculiarities only occur because of the supposition that the observers be stationary with respect to some other distant observer. Observers who fall into the hole are moving with respect to the distant observer, and so perceive the horizon as being in a different location, seeming to recede in front of them so that they never contact it. Increasing tidal forces (and eventual impact with the hole's gravitational singularity) are the only locally noticeable effects. While this seems to allow an infalling observer to relay information from objects outside their perceived horizon but inside the distant observer's perceived horizon, in practice the horizon recedes by an amount small enough that by the time the infalling observer receives any signal from farther into the hole, they've already crossed what the distant observer perceived to be the horizon, and this reception event (and any retransmission) can't be seen by the distant observer.
[edit] Beyond general relativity
The description of event horizons given by general relativity is thought to be incomplete. When the conditions under which event horizons occur are modelled using a more complete picture of the way the universe works, that includes both relativity and quantum mechanics, event horizons are expected to have properties that are different from those predicted using general relativity alone.
At present, it is expected that the primary impact of quantum effects is for event horizons to possess a temperature and so emit radiation. For black holes, this manifests as Hawking radiation, and the larger question of how the black hole possesses a temperature is part of the topic of black hole thermodynamics. For accelerating particles, this manifests as the Unruh effect, which causes space around the particle to appear to be filled with matter and radiation.
A complete description of event horizons is expected to at minimum require a theory of quantum gravity. One such candidate theory is M-theory.
[edit] See also
[edit] References
- The Universe in a Nutshell by Stephen Hawking
- Kip Thorne (1994). Black Holes and Time Warps. W. W. Norton.
- Abhay Ashtekar and Badri Krishnan, “Isolated and Dynamical Horizons and Their Applications”, Living Rev. Relativity, 7, (2004), 10; Online Article, cited Feb.2009.
[edit] More technical references
- ^ S. W. Hawking and G. F. R. Ellis (1975). The large scale structure of space-time. Cambridge University Press.[page number needed]
- ^ Thorne, Kip S.; Misner, Charles; Wheeler, John (1973). Gravitation. W. H. Freeman and Company.[page number needed]
- ^ Wald, Robert M. (1984). General Relativity. Chicago: University of Chicago Press.[page number needed]
- ^ J. A. Peacock (1999). Cosmological Physics. Cambridge University Press.[page number needed]
 |
This section requires expansion. |
