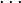Dot product
From Wikipedia, the free encyclopedia
In mathematics, the dot product, also known as the scalar product, is an operation which takes two vectors over the real numbers R and returns a real-valued scalar quantity. It is the standard inner product of the orthonormal Euclidean space. It contrasts with the cross product which produces a vector result.
Contents |
[edit] Definition
The dot product of two vectors a = [a1, a2, … , an] and b = [b1, b2, … , bn] is defined as:
where Σ denotes summation notation and n is the dimension of the vectors.
For example, the dot product of two three-dimensional vectors <1, 3, −5> and <4, −2, −1> is
For two complex column vectors the dot product is defined as
where
is the complex conjugate of bi; further note that in the complex case
The dot product is typically applied to vectors from orthonormal vector spaces. Its generalization to non-orthonormal vector spaces is described below.
[edit] Conversion to matrix multiplication
Using matrix multiplication and treating the vectors as n×1 matrices (i.e. "column matrices" or "column vectors"), the dot product can also be written as:
where aT denotes the transpose of the matrix a, and in this specific case, since a is a column matrix, the transpose of a is a "row matrix" or "row vector" (1×n matrix).
For instance, the dot product of the two above-mentioned three-dimensional vectors is equivalent to the product of a 1×3 matrix by a 3×1 matrix (which, by virtue of the matrix multiplication, results in a 1×1 matrix, i.e., a scalar):
[edit] Geometric interpretation
In Euclidean geometry, the dot product, length, and angle are related. For a vector a, the dot product a · a is the square of the length of a, or
where |a| denotes the length (magnitude) of a. More generally, if b is another vector
where
- |a| and |b| denote the length of a and b
- θ is the angle between them.
Thus, given two vectors, the angle between them can be found by rearranging the above formula:
As the cosine of 90° is zero, the dot product of two orthogonal vectors is always zero:
Moreover, two vectors can be considered orthogonal if and only if their dot product is zero, and they have non-null length. This property provides a simple method to test the condition of orthogonality.
Sometimes these properties are also used for defining the dot product, especially in 2 and 3 dimensions; this definition is equivalent to the above one. For higher dimensions the formula can be used to define the concept of angle.
The geometric properties rely on the basis being orthonormal, i.e. composed of vectors perpendicular to each other and having unit length.
[edit] Scalar projection
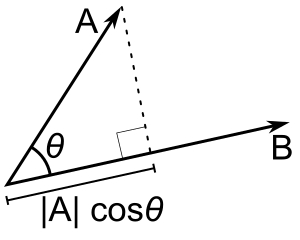
If both a and b have length one (i.e. they are unit vectors), their dot product simply gives the cosine of the angle between them.
If only b is a unit vector, then the dot product a · b gives |a| cos(θ), i.e. the magnitude of the projection of a in the direction of b, with a minus sign if the direction is opposite. This is called the scalar projection of a onto b, or scalar component of a in the direction of b (see figure). This property of the dot product has several useful applications (for instance, see next section).
If neither a nor b is a unit vector, then the magnitude of the projection of a in the direction of b, for example, would be a · (b / |b|) as the unit vector in the direction of b is b / |b|.
[edit] Rotation
A rotation of the orthonormal basis in terms of which vector a is represented is obtained with a multiplication of a by a rotation matrix R. This matrix multiplication is just a compact representation of a sequence of dot products.
For instance, let
- B1 = {x, y, z} and B2 = {u, v, w} be two different orthonormal bases of the same space R3, with B2 obtained by just rotating B1,
- a1 = (ax, ay, az) represent vector a in terms of B1,
- a2 = (au, av, aw) represent the same vector in terms of the rotated basis B2,
- u1, v1, w1 be the rotated basis vectors u, v, w represented in terms of B1.
Then the rotation from B1 to B2 is performed as follows:
Notice that the rotation matrix R is assembled by using the rotated basis vectors u1, v1, w1 as its rows, and these vectors are unit vectors. By definition, Ra1 consists of a sequence of dot products between each of the three rows of R and vector a1. Each of these dot products determines a scalar component of a in the direction of a rotated basis vector (see previous section).
If a1 is a row vector, rather than a column vector, then R must contain the rotated basis vectors in its columns, and must post-multiply a1:
[edit] The dot product in physics
In physics, magnitude is a scalar in the physical sense, i.e. a physical quantity independent of the coordinate system, expressed as the product of a numerical value and a physical unit, not just a number. The dot product is also a scalar in this sense, given by the formula, independent of the coordinate system. The formula in terms of coordinates is evaluated with not just numbers, but numbers times units. Therefore, although it relies on the basis being orthonormal, it does not depend on scaling.
Example:
- Mechanical work is the dot product of force and displacement
[edit] Properties
The following properties hold if a, b, and c are real vectors and r is a scalar.
The dot product is commutative:
The dot product is distributive over vector addition:
The dot product is not associative, but (for column vectors a, b, and c) with the help of the matrix-multiplication one can derive:
The dot product is bilinear:
When multiplied by a scalar value, dot product satisfies:
(these last two properties follow from the first two).
Two non-zero vectors a and b are perpendicular if and only if a • b = 0.
Unlike multiplication of ordinary numbers, where if ab = ac, then b always equals c unless a is zero, the dot product does not obey the cancellation law:
- If a • b = a • c and a ≠ 0:
- then we can write: a • (b − c) = 0 by the distributive law; and from the previous result above:
- If a is perpendicular to (b − c), we can have (b − c) ≠ 0 and therefore b ≠ c.
Provided that the basis is orthonormal, the dot product is invariant under isometric changes of the basis: rotations, reflections, and combinations, keeping the origin fixed. The above mentioned geometric interpretation relies on this property. In other words, for an orthonormal space with any number of dimensions, the dot product is invariant under a coordinate transformation based on an orthogonal matrix. This corresponds to the following two conditions:
- the new basis is again orthonormal (i.e., it is orthonormal expressed in the old one)
- the new base vectors have the same length as the old ones (i.e., unit length in terms of the old basis)
[edit] Derivative
If a and b are functions, then the derivative of a • b is a' • b + a • b'
[edit] Triple product expansion
This is a very useful identity (also known as Lagrange's formula) involving the dot- and cross-products. It is written as
which is easier to remember as “BAC minus CAB”, keeping in mind which vectors are dotted together. This formula is commonly used to simplify vector calculations in physics.
[edit] Proof of the geometric interpretation
Note: This proof is shown for 3-dimensional vectors, but is readily extendable to n-dimensional vectors.
Consider a vector
Repeated application of the Pythagorean theorem yields for its length v
But this is the same as
so we conclude that taking the dot product of a vector v with itself yields the squared length of the vector.
- Lemma 1

Now consider two vectors a and b extending from the origin, separated by an angle θ. A third vector c may be defined as
creating a triangle with sides a, b, and c. According to the law of cosines, we have
Substituting dot products for the squared lengths according to Lemma 1, we get
 (1)
(1)
But as c ≡ a − b, we also have
 ,
,
which, according to the distributive law, expands to
 (2)
(2)
Merging the two c • c equations, (1) and (2), we obtain
Subtracting a • a + b • b from both sides and dividing by −2 leaves
[edit] Generalization
The inner product generalizes the dot product to abstract vector spaces and is normally denoted by <a , b>. Due to the geometric interpretation of the dot product the norm ||a|| of a vector a in such an inner product space is defined as
such that it generalizes length, and the angle θ between two vectors a and b by
In particular, two vectors are considered orthogonal if their inner product is zero
The Frobenius inner product generalizes the dot product to matrices. It is defined as the sum of the products of the corresponding components of two matrices having the same size.
[edit] Matrix representation
An inner product can be represented using a square matrix and matrix multiplication. For example, given two vectors
with respect to the basis set S
any inner product can be represented as follows:
where M is a 3x3 matrix. Given the matrix of the inner products through S called CS, M can be calculated by solving the following system of equations.

If the basis set S is composed of orthogonal unit vectors (orthonormal basis), then both CS and M reduce to the identity matrix 1, and the inner product can be represented as a simple product between a row matrix and a column matrix:
Thus, if the basis is orthonormal, the square matrix M is not necessary and the inner product coincides with the dot product as defined above:
[edit] Example
Given a basis set
and a matrix of the inner product through S
we can set each element of CS equal to the inner product of two of the basis vectors as follows
which gives nine equations and nine unknowns. Solving these equations yields
[edit] See also
[edit] External links
- Eric W. Weisstein, Dot product at MathWorld.
- Interactive GeoGebra Applet
- Java demonstration of dot product
- Another Java demonstration of dot product
- Explanation of dot product including with complex vectors
- "Dot Product" by Bruce Torrence, Wolfram Demonstrations Project, 2007.
|
|||||
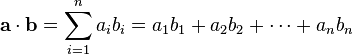

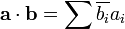




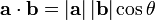


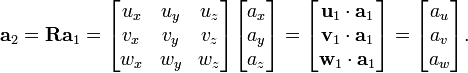






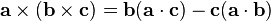



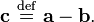




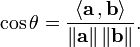





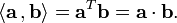


![\mathbf{C}_S[i,j] = \langle \mathrm{S}[i],\mathrm{S}[j] \rangle](http://upload.wikimedia.org/math/7/4/f/74f1e71fe5e466587e07a33015b4c0e7.png)
![\mathbf{C}_S[0,0] = 5 = \langle \mathbf{u,u} \rangle =
\begin{bmatrix} 1 & 0 & 0 \end{bmatrix}
\mathrm{M}
\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}](http://upload.wikimedia.org/math/1/9/f/19fdf9cc0ff058652e69823d5b7f78d5.png)
![\mathbf{C}_S[0,1] = 2 = \langle \mathbf{u,v} \rangle =
\begin{bmatrix} 1 & 0 & 0 \end{bmatrix}
\mathrm{M}
\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}](http://upload.wikimedia.org/math/c/8/3/c837aed0e110a77cca923bf8414ed3b3.png)