F-distribution

Fisher-Snedecor
	Probability density function;
	Cumulative distribution function;
Parameters	deg. of freedom
Support
Probability density function (pdf)
Cumulative distribution function (cdf)
Mean	for d2 > 2
Median
Mode	for d1 > 2
Variance	for d2 > 4
Skewness	; for d2 > 6
Excess kurtosis	see text
Entropy
Moment-generating function (mgf)	does not exist, raw moments defined elsewhere
Characteristic function	defined elsewhere

In probability theory and statistics, the F-distribution is a continuous probability distribution.^[1]^[2]^[3] It is also known as Snedecor's F distribution or the Fisher-Snedecor distribution (after R.A. Fisher and George W. Snedecor). The F-distribution arises frequently as the null distribution of a test statistic, especially in likelihood-ratio tests, perhaps most notably in the analysis of variance; see F-test.

[edit] Characterization

A random variate of the F-distribution arises as the ratio of two chi-squared variates:

$\frac{U_1/d_1}{U_2/d_2}$

where

U₁ and U₂ have chi-square distributions with d₁ and d₂ degrees of freedom respectively, and

The probability density function of an F(d₁, d₂) distributed random variable is given by

$f(x) = \frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\!$

for real x ≥ 0, where d₁ and d₂ are positive integers, and B is the beta function.

The cumulative distribution function is $F(x)=I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)$

The expectation, variance, and other details about the $F (d 1, d 2)$ are given in the sidebox; for $d 2 > 8$ , the kurtosis is

$\frac{20d_2-8d_2^2+d_2^3+44d_1-32d_1d_2+A}{d_1(d_2-6)(d_2-8)(d_1+d_2-2)/12}$

where $A=5d_2^2d_1-22d_1^2+5d_2d_1^2-16.$

A generalization of the (central) F-distribution is the noncentral F-distribution.

If $X \sim \mathrm{F}(\nu_1, \nu_2)$ then $Y = \lim_{\nu_2 \to \infty} \nu_1 X$ has the chi-square distribution $\chi^2_{\nu_{1}}$
$\operatorname{F}(\nu_1,\nu_2)$ is equivalent to the scaled Hotelling's T-square distribution $(\nu_1(\nu_1+\nu_2-1)/\nu_2)\operatorname{T}^2(\nu_1,\nu_1+\nu_2-1)$ .
If $X \sim \operatorname{F}(\nu_1,\nu_2),$ then $\frac{1}{X} \sim F(\nu_2,\nu_1)$ .
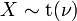if $X \sim \mathrm{t}(\nu)\!$ has a Student's t-distribution then $X^2 \sim \operatorname{F}(\nu_1 = 1, \nu_2 = \nu)$ .
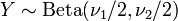if $X \sim \operatorname{F}(\nu_1,\nu_2)$ and $Y=\frac{\nu_1 X/\nu_2}{1+\nu_1 X/\nu_2}$ then $Y \sim \operatorname{Beta}(\nu_1/2,\nu_2/2)$ has a Beta-distribution.
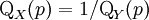if $\operatorname{Q}_X(p)$ is the quantile $p$ for $X\sim \operatorname{F}(\nu_1,\nu_2)$ and $\operatorname{Q}_Y(p)$ is the quantile $p$ for $Y\sim \operatorname{F}(\nu_2,\nu_1)$ then $\operatorname{Q}_X(p)=1/\operatorname{Q}_Y(p)$ .

^ ^a ^b ^c Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 26", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, ISBN 0-486-61272-4 .
^ NIST (2006). Engineering Statistics Handbook - F Distribution
^ Mood, Alexander; Franklin A. Graybill, Duane C. Boes (1974). Introduction to the Theory of Statistics (Third Edition, p. 246-249). McGraw-Hill. ISBN 0-07-042864-6.

Probability density function
Cumulative distribution function
Parameters	$d_1>0,\ d_2>0$ deg. of freedom
Support	$x \in [0, +\infty)\!$
Probability density function (pdf)	$\frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\!$
Cumulative distribution function (cdf)	$I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)\!$
Mean	$\frac{d_2}{d_2-2}\!$ for $d 2 > 2$
Median
Mode	$\frac{d_1-2}{d_1}\;\frac{d_2}{d_2+2}\!$ for $d 1 > 2$
Variance	$\frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!$ for $d 2 > 4$
Skewness	$\frac{(2 d_1 + d_2 - 2) \sqrt{8 (d_2-4)}}{(d_2-6) \sqrt{d_1 (d_1 + d_2 -2)}}\!$ for $d 2 > 6$
Excess kurtosis	see text
Entropy
Moment-generating function (mgf)	does not exist, raw moments defined elsewhere^[1]
Characteristic function	defined elsewhere^[1]