From Wikipedia, the free encyclopedia
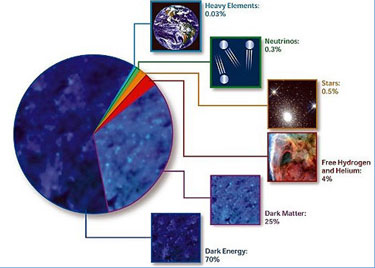
A
pie chart indicating the proportional composition of different energy-density components of the universe. Roughly ninety-five percent is exotic
dark matter and
dark energy.
ΛCDM or Lambda-CDM is an abbreviation for Lambda-Cold Dark Matter. It is frequently referred to as the concordance model of big bang cosmology, since it attempts to explain cosmic microwave background observations, as well as large scale structure observations and supernovae observations of the accelerating expansion of the universe. It is the simplest known model that is in general agreement with observed phenomena.
- Λ (Lambda) stands for the cosmological constant which is a dark energy term that allows for the current accelerating expansion of the universe. The cosmological constant is often described in terms of ΩΛ, the fraction of the energy density of a flat Universe in the form of the cosmological constant. Currently,
0.74, implying 74% of the energy density of the present universe is in this form.
- Cold dark matter is the model where the dark matter is explained as being cold (i.e. its velocity is non-relativistic (v<<c) at the epoch of radiation-matter equality), possibly non-baryonic, dissipationless (can not cool by radiating photons) and collisionless (i.e., the dark matter particles interact with each other and other particles only through gravity). This component makes up 22% of the energy density of the present universe. The remaining 4% is all of the matter (and energy) that makes up the atoms (and photons) that are the building blocks of planets, stars, and gas clouds in the universe.
These are the simplest assumptions for a consistent, physical model of cosmology. However, ΛCDM is a model. Cosmologists anticipate that all of these assumptions will not be borne out exactly, after more is learned about the applicable fundamental physics. In particular, cosmic inflation predicts spatial curvature at the level of 10−4 to 10−5. It would also be surprising if the temperature of dark matter were absolute zero. Moreover, ΛCDM says nothing about the fundamental physical origin of dark matter, dark energy and the nearly scale-invariant spectrum of primordial curvature perturbations: in that sense, it is merely a useful parameterization of ignorance.
[edit] Parameters
The model has six parameters. The Hubble constant determines the rate of expansion of the universe, as well as the critical density for closure of the universe, ρ0. Densities for baryons, dark matter and dark energy are given as Ωs, which are the ratio of the true density to the critical density: e.g. Ωb = ρb / ρ0. Since the ΛCDM model assumes a spatially flat universe, these densities sum to one, and the density of dark energy is not a free parameter. The optical depth to reionization determines the redshift of reionization. Information about the density fluctuations is determined by the amplitude of the primordial fluctuations (from cosmic inflation) and the spectral index, which measures how the fluctuations change with scale (ns = 1 corresponds to a scale-invariant spectrum).
The errors quoted are 1σ: that is, there is statistically a 68% likelihood that the true value falls within the upper and lower error bounds. The errors are not Gaussian, and they have been derived using a Markov chain Monte Carlo analysis by the Wilkinson Microwave Anisotropy Probe collaboration (Spergel et al. 2006) which also uses Sloan Digital Sky Survey and Type Ia supernova data.
[edit] Extended models
Possible extensions of the simplest ΛCDM model are to allow quintessence rather than a cosmological constant. In this case, the equation of state of dark energy is allowed to differ from −1. Cosmic inflation predicts tensor fluctuations (gravitational waves). Their amplitude is parameterized by the tensor-to-scalar ratio, which is determined by the energy scale of inflation. Other modifications allow for spatial curvature or a running spectral index, which are generally viewed as inconsistent with cosmic inflation.
Allowing these parameters will generally increase the errors in the parameters quoted above, and may also shift the observed values somewhat.
| Parameter |
Value |
Description |
| w |
 |
Equation of state |
| r |
< 0.55 (2σ) |
Tensor-to-scalar ratio |
| Ωk |
 |
Spatial curvature |
| α |
 |
Running of the spectral index |
| Σmν |
< 0.87 eV (2σ) |
Summed neutrino masses |
These are consistent with a cosmological constant, w = − 1, and no spatial curvature Ωk = 0. Some have suggested that there is a running spectral index, but no statistically significant study has revealed one. Theoretical expectations suggest that the tensor-to-scalar ratio r should be between 0 and 0.3, and so should be tested in the near future.
[edit] References
- D. N. Spergel et al. (WMAP collaboration) (March 2006). Wilkinson Microwave Anisotropy Probe (WMAP) three year results: implications for cosmology. http://lambda.gsfc.nasa.gov/product/map/current/map_bibliography.cfm.
- M. Tegmark et al. (SDSS collaboration), Cosmological Parameters from SDSS and WMAP, Phys. Rev. D69 103501 (2004).
- D. N. Spergel et al. (WMAP collaboration), First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: determination of cosmological parameters, Astrophys. J. Suppl. 148 175 (2003).
- R. Rebolo et al. (VSA collaboration), Cosmological parameter estimation using Very Small Array data out to l=1500, Monthly Notices of the Royal Astronomical Society, Volume 353, Issue 3, pp. 747-759
- J. P. Ostriker and P. J. Steinhardt, Cosmic Concordance, arXiv:astro-ph/9505066.
[edit] See also
km s-1 Mpc-1
kg/m3
years
