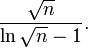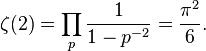Prime number

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Divisibility-based
sets of integers
Form of factorization:
Prime number
Composite number
Powerful number
Square-free number
Achilles number
Constrained divisor sums:
Perfect number
Almost perfect number
Quasiperfect number
Multiply perfect number
Hyperperfect number
Superperfect number
Unitary perfect number
Semiperfect number
Primitive semiperfect number
Practical number
Numbers with many divisors:
Abundant number
Highly abundant number
Superabundant number
Colossally abundant number
Highly composite number
Superior highly composite number
Other:
Deficient number
Weird number
Amicable number
Friendly number
Sociable number
Solitary number
Sublime number
Harmonic divisor number
Frugal number
Equidigital number
Extravagant number
See also:
Divisor function
Divisor
Prime factor
Factorization
This box: view • talk • edit

In mathematics, a prime number (or a prime) is a natural number which has exactly two distinct natural number divisors: 1 and itself. An infinitude of prime numbers exists, as demonstrated by Euclid around 300 BC. The first twenty-five prime numbers are:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 (sequence A000040 in OEIS).

See the list of prime numbers for a longer list. The number 1 is by definition not a prime number. The set of prime numbers is sometimes denoted by \mathbb{P}.

The property of being a prime is called primality, and the word prime is also used as an adjective. Since 2 is the only even prime number, the term odd prime refers to any prime number greater than 2.

The study of prime numbers is part of number theory. Prime numbers have been the subject of intense research, yet some fundamental questions, such as the Riemann hypothesis and the Goldbach conjecture, have been unresolved for more than a century. The problem of modelling the distribution of prime numbers is a popular subject of investigation for number theorists: when looking at individual numbers, the primes seem to be randomly distributed, but the “global” distribution of primes follows well-defined laws.

The notion of prime number has been generalized in many different branches of mathematics:

  • In ring theory, a branch of abstract algebra, the term “prime element” has a specific meaning. Here, a non-zero, non-unit ring element a is defined to be prime if whenever a divides bc for ring elements b and c, then a divides at least one of b or c. With this meaning, the additive inverse of any prime number is also prime. In other words, when considering the set of integers as a ring, −7 is a prime element. Without further specification, however, “prime number” always means a positive integer prime. Among rings of complex algebraic integers, Eisenstein primes and Gaussian primes may also be of interest.
  • In knot theory, a prime knot is a knot which can not be written as the knot sum of two lesser nontrivial knots.

Contents

[edit] Prime numbers and the fundamental theorem of arithmetic

Main article: Fundamental theorem of arithmetic

A natural number is called a prime, a prime number or just prime if it has exactly two distinct divisors. Otherwise it is called composite. Therefore, 1 is not prime, since it has only one divisor, namely 1. However, 2 and 3 are prime, since they have exactly two divisors, namely 1 and 2, and 1 and 3, respectively. Next, 4, is composite, since it has 3 divisors: 1, 2, and 4.

Using symbols, a number n > 1 is prime if it cannot be written as a product of two factors a and b, both of which are bigger than 1:

n = a · b.

The crucial importance of prime numbers to number theory and mathematics in general stems from the fundamental theorem of arithmetic which states that every positive integer larger than 1 can be written as a product of one or more primes in a way which is unique except possibly for the order of the prime factors. Primes can thus be considered the “basic building blocks” of the natural numbers. For example, we can write

23244 = 2 · 2 · 3 · 13 · 149 = 22 · 3 · 13 · 149. (22 denotes the square or second power of 2.)

As in this example, the same prime factor may occur multiple times. A decomposition

n = p1 · p2 · ... · pt

of a number n into (finitely many) prime factors p1, p2, ... to pt is called prime factorization of n. The fundamental theorem of arithmetic can be rephrased so as to say that any factorization into primes will be identical except for the order of the factors. So, albeit there are many prime factorization algorithms to do this in practice for larger numbers, they all have to yield the same result.

[edit] Examples and first properties

Illustration showing that 11 is a prime number while 12 is not.

The image at the right shows a graphical way to show that 12 is not prime. More generally, all prime numbers except 2 and 5, written in the usual decimal system, end in 1, 3, 7 or 9, since numbers ending in 0, 2, 4, 6 or 8 are multiples of 2 and numbers ending in 0 or 5 are multiples of 5. Similarly, all prime numbers above 3 are of the form 6n − 1 or 6n + 1, because all other numbers are divisible by 2 or 3. Generalizing this, all prime numbers above q are of form q#·n + m, where 0 < m < q, and m has no prime factor ≤ q.

If p is a prime number and p divides a product ab of integers, then p divides a or p divides b. This proposition is known as Euclid's lemma. It is used in some proofs of the uniqueness of prime factorizations.

[edit] Primality of one

The importance of this theorem is one of the reasons for the exclusion of 1 from the set of prime numbers. If 1 were admitted as a prime, the precise statement of the theorem would require additional qualifications, since 3 could then be decomposed in different ways

3 = 1 · 3 and 3 = 1 · 1 · 1 · 3 = 13 · 3.

Until the 19th century, most mathematicians considered the number 1 a prime, with the definition being just that a prime is divisible only by 1 and itself but not requiring a specific number of distinct divisors. There is still a large body of mathematical work that is valid despite labelling 1 a prime, such as the work of Stern and Zeisel. Derrick Norman Lehmer's list of primes up to 10,006,721, reprinted as late as 1956,[1] started with 1 as its first prime.[2] Henri Lebesgue is said to be the last professional mathematician to call 1 prime.[citation needed] The change in label occurred so that the fundamental theorem of arithmetic, as stated, is valid, i.e., “each number has a unique factorization into primes.”[3][4] Furthermore, the prime numbers have several properties that the number 1 lacks, such as the relationship of the number to its corresponding value of Euler's totient function or the sum of divisors function.[5]

[edit] History

The Sieve of Eratosthenes is a simple, ancient algorithm for finding all prime numbers up to a specified integer. It is the predecessor to the modern Sieve of Atkin, which is faster but more complex. The eponymous Sieve of Eratosthenes was created in the 3rd century BC by Eratosthenes, an ancient Greek mathematician.

There are hints in the surviving records of the ancient Egyptians that they had some knowledge of prime numbers: the Egyptian fraction expansions in the Rhind papyrus, for instance, have quite different forms for primes and for composites. However, the earliest surviving records of the explicit study of prime numbers come from the Ancient Greeks. Euclid's Elements (circa 300 BC) contain important theorems about primes, including the infinitude of primes and the fundamental theorem of arithmetic. Euclid also showed how to construct a perfect number from a Mersenne prime. The Sieve of Eratosthenes, attributed to Eratosthenes, is a simple method to compute primes, although the large primes found today with computers are not generated this way.

After the Greeks, little happened with the study of prime numbers until the 17th century. In 1640 Pierre de Fermat stated (without proof) Fermat's little theorem (later proved by Leibniz and Euler). A special case of Fermat's theorem may have been known much earlier by the Chinese. Fermat conjectured that all numbers of the form 22n + 1 are prime (they are called Fermat numbers) and he verified this up to n = 4 (or 216 + 1). However, the very next Fermat number 232 + 1 is composite (one of its prime factors is 641), as Euler discovered later, and in fact no further Fermat numbers are known to be prime. The French monk Marin Mersenne looked at primes of the form 2p − 1, with p a prime. They are called Mersenne primes in his honor.

Euler's work in number theory included many results about primes. He showed the infinite series 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + … is divergent. In 1747 he showed that the even perfect numbers are precisely the integers of the form 2p−1(2p − 1), where the second factor is a Mersenne prime.

At the start of the 19th century, Legendre and Gauss independently conjectured that as x tends to infinity, the number of primes up to x is asymptotic to x/ln(x), where ln(x) is the natural logarithm of x. Ideas of Riemann in his 1859 paper on the zeta-function sketched a program which would lead to a proof of the prime number theorem. This outline was completed by Hadamard and de la Vallée Poussin, who independently proved the prime number theorem in 1896.

Proving a number is prime is not done (for large numbers) by trial division. Many mathematicians have worked on primality tests for large numbers, often restricted to specific number forms. This includes Pépin's test for Fermat numbers (1877), Proth's theorem (around 1878), the Lucas–Lehmer test for Mersenne numbers (originated 1856),[6] and the generalized Lucas–Lehmer test. More recent algorithms like APRT-CL, ECPP and AKS work on arbitrary numbers but remain much slower.

For a long time, prime numbers were thought to have extremely limited application outside of pure mathematics;[citation needed] this changed in the 1970s when the concepts of public-key cryptography were invented, in which prime numbers formed the basis of the first algorithms such as the RSA cryptosystem algorithm.

Since 1951 all the largest known primes have been found by computers. The search for ever larger primes has generated interest outside mathematical circles. The Great Internet Mersenne Prime Search and other distributed computing projects to find large primes have become popular in the last ten to fifteen years, while mathematicians continue to struggle with the theory of primes.

[edit] Arithmetic modulo a prime p

Main article: Modular arithmetic

Modular arithmetic is a modification of usual arithmetic, by doing all calculations "modulo" a fixed number n. All calculations of modular arithmetic take place in the finite set

{0, 1, 2, ..., n − 1}.

Calculating modulo n means that sums, differences and products are calculated as usual, but then only the remainder after division by n is considered. For example, let n = 7. Then, in modular arithmetic modulo 7, the sum 3 + 5 is 1 instead of 8, since 8 divided by 7 has remainder 1. Similarly, 6 + 1 = 0 modulo 7, 2 − 5 = 4 modulo 7 (since −3 + 7 = 4) and 3 · 4 = 5 modulo 7 (12 has remainder 5). The set {0, 1, 2, ..., n − 1}, with this modified addition and multiplication is denoted Z/nZ for all n. Standard properties of addition and multiplication familiar from the number system of the integers or rational numbers remain valid, for example

(a + b) · c = a · c + b · c (law of distributivity).

(In the parlance of abstract algebra, Z/nZ is a ring.) In general it is, however not possible to divide in this setting. For example, for n = 6, the equation

3 · x = 2 (modulo 6),

a solution x of which would be an analogue of 2/3, cannot be solved, as one can see by calculating 3 · 0, ..., 3 · 5 modulo 6.

The distinctive feature of prime numbers is the following: division is possible in modular arithmetic if and only if n is a prime. For n = 7, the equation

3 · x = 2 (modulo 7)

has a unique solution, x = 3. In abstract algebra, Z/pZ is called a finite field. Equivalently, n is prime if and only if all integers m satisfying 2 ≤ m ≤ n − 1 are coprime to n, i.e., their greatest common divisor is 1. Using Euler's totient function, n is prime if and only if φ(n) = n − 1.

A number of theorems can be derived from inspecting Z/pZ in an abstract way, for any prime p. For example Fermat's little theorem: if a is any integer, then ap − a is divisible by p. A consequence of this is the following: if p is a prime number other than 2 and 5, 1/p is always a recurring decimal, whose period is p − 1 or a divisor of p − 1. This can be deduced directly from Fermat's little theorem. 1/p expressed likewise in base q (rather than base 10) has similar effect, provided that p is not a prime factor of q. The article on recurring decimals shows some of the interesting properties. Wilson's theorem says that an integer p > 1 is prime if and only if the factorial (p − 1)! + 1 is divisible by p. Conversely, an integer n > 4 is composite if and only if (n − 1)! is divisible by n.

[edit] The number of prime numbers

[edit] There are infinitely many prime numbers

The oldest known proof for the statement that there are infinitely many prime numbers is given by the Greek mathematician Euclid in his Elements (Book IX, Proposition 20). Euclid states the result as "there are more than any given [finite] number of primes", and his proof is essentially the following:

Consider any finite set of primes. Multiply all of them together and add 1 (see Euclid number). The resulting number is not divisible by any of the primes in the finite set we considered, because dividing by any of these would give a remainder of 1. Because all non-prime numbers can be decomposed into a product of underlying primes, then either this resultant number is prime itself, or there is a prime number or prime numbers which the resultant number could be decomposed into but are not in the original finite set of primes. Either way, there is at least one more prime that was not in the finite set we started with. This argument applies no matter what finite set we began with. So there are more primes than any given finite number.

This previous argument explains why the product P of finitely many primes plus 1 must be divisible by some prime (possibly itself) not among those finitely many primes.

The proof is sometimes phrased in a way that falsely leads some readers to think that P + 1 must itself be prime, and think that Euclid's proof says the prime product plus 1 is always prime. This confusion arises when the proof is presented as a proof by contradiction and P is assumed to be the product of the members of a finite set containing all primes. Then it is asserted that if P + 1 is not divisible by any members of that set, then it is not divisible by any primes and "is therefore itself prime" (quoting G. H. Hardy[7]). This sometimes leads readers to conclude mistakenly that if P is the product of the first n primes then P + 1 is prime. That conclusion relies on a hypothesis later proved false, and so cannot be considered proved. The smallest counterexample with composite P + 1 is (2 × 3 × 5 × 7 × 11 × 13) + 1 = 30,031 = 59 × 509 (both primes). See also Euclid's theorem.

Adding the reciprocals of all primes together results in a divergent infinite series (proof). More precisely, if S(x) denotes the sum of the reciprocals of all prime numbers p with p ≤ x, then S(x) = ln ln x + O(1) for x → ∞. This was shown by Euler.

Another proof based on Fermat numbers was given by Goldbach.[8] Kummer's is particularly elegant[9] and Harry Furstenberg provides one using general topology.[10]

In every arithmetic progression a, a + q, a + 2q, a + 3q, … where the positive integers a and q are coprime, there are infinitely many primes (Dirichlet's theorem on arithmetic progressions).

[edit] Verifying primality

Main article: Primality test

In order to use primes, verifying that a given number n is prime or not is of crucial interest. There are several ways to achieve this aim. The most basic method known as trial division works as follows: given a number n, one divides n by all numbers m less than or equal to the square root of that number. If any of the divisions come out as an integer, then the original number is not a prime. Otherwise, it is a prime. Actually it suffices to do these trial divisions for m prime, only. While an easy algorithm, it quickly becomes impractical for testing large integers because the number of possible factors grows too rapidly as the number-to-be-tested increases: The number of prime numbers less than n is near n / (ln (n) − 1). So, to check n for primality the largest prime factor needed is just less than 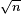\scriptstyle\sqrt{n}, and so the number of such prime factor candidates would be close to

\frac {\sqrt{n}}{\ln\sqrt{n} - 1}.

This increases ever more slowly with n, but, because there is interest in large values for n, the count is large also: for n = 10 20 it is 450 million.

The sieve of Eratosthenes (see above) is related, simple way to compute all prime numbers up to a given limit, but it is similarly slow. The modern sieve of Atkin is more complicated, but faster when properly optimized. In practice one often wants to check whether a given number is prime, rather than generate a list of primes as the two mentioned sieve algorithms do.

Primality test algorithms can be divided into two main classes, deterministic and probabilistic algorithms. Probabilistic algorithms may report a composite number as a prime, but certainly does not identify primes as composite numbers; deterministic algorithms on the other hand do not have the possibility of such erring. The interest of probabilistic algorithms lies in the fact that they are often quicker than deterministic ones; in addition for most such algorithms the probability of erroneously identifying a composite number as prime is known. They typically pick a random number a called a "witness" and check some formula involving the witness and the potential prime n. After several iterations, they declare n to be "definitely composite" or "probably prime". For example, Fermat's primality test relies on Fermat's little theorem (see above). Thus, if

ap − 1 (mod p)

is unequal to 1, p is definitely composite. However, p may be composite even if ap − 1 = 1 (mod p) for all witnesses a, namely when p is a Carmichael number. In general, composite numbers that will be declared probably prime no matter what witness is chosen are called pseudoprimes for the respective test. However, the most popular probabilistic tests do not suffer from this drawback.

[edit] Special types of primes

Further information: List of prime numbers
Construction of a regular pentagon. 5 is a Fermat prime.

There are many particular types of primes, for example qualified by various formulae, or by considering its decimal digits. Primes of the form 2p − 1, where p is a prime number, are known as Mersenne primes. Their importance lies in the fact that there are comparatively quick algorithms testing primality for Mersenne primes. Primes of the form 22n + 1 are known as Fermat primes; a regular n-gon is constructible using straightedge and compass if and only if

n = 2i · p

where p is a Fermat prime and i is any natural number, including zero. Only four Fermat primes are known: 3, 5, 17, 257, and 65,537. Prime numbers p where 2p + 1 is also prime are known as Sophie Germain primes. A prime p is called primorial or prime-factorial if it has the form

p = n# ± 1

for some number n, where n# stands for the product 2 · 3 · 5 · 7 · … of all the primes ≤ n. A prime is called factorial if it is of the form n! ± 1. It is not known whether there are infinitely many primorial or factorial primes.

[edit] Location of the largest known prime

Main articles: Largest known prime and Mersenne prime

Historically, the largest known prime has almost always been a Mersenne prime since the dawn of electronic computers, because there exists a particularly fast primality test for numbers of this form, the Lucas–Lehmer test for Mersenne numbers. The following table gives the largest known primes of the mentioned types.

Prime Number of decimal digits Type Date Found by
243,112,609 − 1 12,978,189 Mersenne prime (46th) August 23, 2008 Great Internet Mersenne Prime Search
19,249 × 213,018,586 + 1 3,918,990 not a Mersenne prime (Proth number) March 26, 2007 Seventeen or Bust
392113# + 1 169,966 primorial prime 2001 Heuer[11]
34790! − 1 142,891 factorial prime 2002 Marchal, Carmody and Kuosa [12]
2003663613 · 2195000 ± 1 58,711 twin primes 2007 Twin prime search [13]

Some of the largest primes not known to have any particular form (that is, no simple formula such as that of Mersenne primes) have been found by taking a piece of semi-random binary data, converting it to a number n, multiplying it by 256k for some positive integer k, and searching for possible primes within the interval [256kn + 1, 256k(n + 1) − 1].

The Electronic Frontier Foundation has offered a US$100,000 prize to the first discoverers of a prime with at least 10 million digits. The price may be awarded to GIMPS and the UCLA mathematics department for discovering the 46th Mersenne prime mentioned in the table.[1][2] They also offer $150,000 and $250,000 for 100 million digits and 1 billion digits, respectively.

[edit] Generating prime numbers

Main article: Formula for primes

There is no known formula for primes which is more efficient at finding primes than the methods mentioned above under “Finding prime numbers”.

There is a set of Diophantine equations in 9 variables and one parameter with the following property: the parameter is prime if and only if the resulting system of equations has a solution over the natural numbers. This can be used to obtain a single formula with the property that all its positive values are prime.

There is no polynomial, even in several variables, that takes only prime values. However, there are polynomials in several variables, whose positive values (as the variables take all positive integer values) are exactly the primes (for an example, see formula for primes).

Another formula is based on Wilson's theorem mentioned above, and generates the number 2 many times and all other primes exactly once. There are other similar formulas which also produce primes.

[edit] Distribution

Further information: Prime number theorem
The Ulam spiral. Black pixels show prime numbers.

Given the fact that there is an infinity of primes, it is natural to seek for patterns or irregularities in the distribution of primes. The problem of modeling the distribution of prime numbers is a popular subject of investigation for number theorists. The occurrence of individual prime numbers among the natural numbers is (so far) unpredictable, even though there are laws (such as the prime number theorem and Bertrand's postulate) that govern their average distribution. Leonhard Euler commented

Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the mind will never penetrate.[14]

In a 1975 lecture, Don Zagier commented

There are two facts about the distribution of prime numbers of which I hope to convince you so overwhelmingly that they will be permanently engraved in your hearts. The first is that, despite their simple definition and role as the building blocks of the natural numbers, the prime numbers grow like weeds among the natural numbers, seeming to obey no other law than that of chance, and nobody can predict where the next one will sprout. The second fact is even more astonishing, for it states just the opposite: that the prime numbers exhibit stunning regularity, that there are laws governing their behavior, and that they obey these laws with almost military precision.[15]

Euler noted that the function

n2 + n + 41

gives prime numbers for n ≤ 40 (but not necessarily so for bigger n), a remarkable fact leading into deep algebraic number theory, more specifically Heegner numbers. The Ulam spiral depicts all natural numbers in a spiral-like way. Surprisingly, prime numbers cluster on certain diagonals and not others.

[edit] The number of prime numbers below a given number

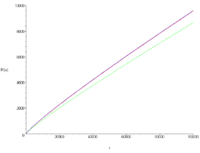
Main article: Prime counting function
A chart depicting π(n) (blue), n / ln (n) (green) and Li (n), the offset logarithmic integral (red).

The prime-counting function π(n) is defined as the number of primes up to n. For example π(11) = 5, since there are five primes less or equal to 11. There are known algorithms to compute exact values of π(n) faster than it would be possible to compute each prime up to n. Values as large as π(1020) can be calculated quickly and accurately with modern computers.

For larger values of n, beyond the reach of modern equipment, the prime number theorem provides an estimate: π(n) is approximately n/ln(n). In other words, as n gets very large, the likelihood that a number less than n is prime is inversely proportional to the number of digits in n. Even better estimates are known; see for example Prime number theorem#The prime-counting function in terms of the logarithmic integral.

If n is a positive integer greater than 1, then there is always a prime number p with n < p < 2n (Bertrand's postulate).

[edit] Gaps between primes

Main article: Prime gap

A sequence of consecutive integers none of which is prime constitutes a prime gap. There are arbitrarily long prime gaps: for any natural number n larger than 1, the sequence (for the notation n! read factorial)

n! + 2, n! + 3, …, n! + n

is a sequence of n − 1 consecutive composite integers, since

n! + m = m · (1 · 2 · … · (m − 1) · (m + 1) … n + 1)

is composite for any 2 ≤ m ≤ n. On the other hand, the gaps get arbitrarily small in proportion to the primes: the quotient

(pi + 1 − pi) / pi,

where pi denotes the ith prime number (i.e., p1 = 2, p2 = 3, etc.), approaches zero as i approaches infinity.

[edit] Open questions

[edit] The Riemann hypothesis

Main article: Riemann hypothesis

To state the Riemann hypothesis, one of the oldest, yet, as of 2009, unproven mathematical conjectures, it is necessary to understand the Riemann zeta function (s is a complex number with real part bigger than 1)

\zeta(s)=\sum_{n=1}^\infin \frac{1}{n^s} = \prod_{p} \frac{1}{1-p^{-s}}.

The second equality is a consequence of the fundamental theorem of arithmetics, and shows that the zeta function is deeply connected with prime numbers. For example, the fact (see above) that there are infinitely many primes can be read off from the divergence of the harmonic series:

\zeta(1) = \sum_{n=1}^\infin \frac{1}{n} = \prod_{p} \frac{1}{1-p^{-1}} = \infty

Another example of the richness of the zeta function and a glimpse of modern algebraic number theory is the following identity (Basel problem), due to Euler,

\zeta(2) = \prod_{p} \frac{1}{1-p^{-2}}= \frac{\pi^2}{6}.

Riemann's hypothesis is concerned with the zeroes of the ζ-function (i.e., s such that ζ(s) = 0). The connection to prime numbers is that it essentially says that the primes are as regularly distributed as possible. From a physical viewpoint, it roughly states that the irregularity in the distribution of primes only comes from random noise. From a mathematical viewpoint, it roughly states that the asymptotic distribution of primes (about 1/ log x of numbers less than x are primes, the prime number theorem) also holds for much shorter intervals of length about the square root of x (for intervals near x). This hypothesis is generally believed to be correct. In particular, the simplest assumption is that primes should have no significant irregularities without good reason.

[edit] Other conjectures

Further information: Category:Conjectures about prime numbers

Besides the Riemann hypothesis, there are many more conjectures about prime numbers, many of which are old: for example, all four of Landau's problems from 1912 (the Goldbach, twin prime, Legendre conjecture and conjecture about n2+1 primes) are still unsolved.

Many conjectures deal with the question whether an infinity of prime numbers subject to certain constraints exists. For example, it is conjectured that there are infinitely many twin primes, pairs of primes with difference 2 (twin prime conjecture). Polignac's conjecture is a strengthening of that conjecture, it states that for every positive integer n, there are infinitely many pairs of consecutive primes which differ by 2n. It is conjectured there are infinitely many primes of the form n2 + 1.[16] These conjectures are special cases of the broad Schinzel's hypothesis H.[citation needed]

It is conjectured that there are infinitely many Fibonacci primes[17] and infinitely many Mersenne primes, but not Fermat primes.[18] It is not known whether or not there are an infinite number of prime Euclid numbers.

Other conjectures relate the additive aspects of numbers with prime numbers: Goldbach's conjecture asserts that every even integer greater than 2 can be written as a sum of two primes, while the weak version states that every odd integer greater than 5 can be written as a sum of three primes.

  • Legendre's conjecture: There is a prime number between n2 and (n + 1)2 for every positive integer n.
  • Cramér's conjecture: \limsup_{n\rightarrow\infty} \frac{p_{n+1}-p_n}{(\log p_n)^2} = 1. This conjecture implies Legendre's, but its status is more unsure.
  • Brocard's conjecture: There are always at least four primes between the squares of consecutive primes greater than 2.

[edit] Applications

For a long time, number theory in general, and the study of prime numbers in particular, was seen as the canonical example of pure mathematics, with no applications outside of the self-interest of studying the topic. In particular, number theorists such as British mathematician G. H. Hardy prided themselves on doing work that had absolutely no military significance.[19] However, this vision was shattered in the 1970s, when it was publicly announced that prime numbers could be used as the basis for the creation of public key cryptography algorithms. Prime numbers are also used for hash tables and pseudorandom number generators.

Some rotor machines were designed with a different number of pins on each rotor, with the number of pins on any one rotor either prime, or coprime to the number of pins on any other rotor. This helped generate the full cycle of possible rotor positions before repeating any position.

Many mathematical domains make great use of prime numbers. An example from the theory of finite groups are the Sylow theorems: if G is a finite group and pn is the highest power of the prime p which divides the order of G, then G has a subgroup of order pn. Also, any group of prime order is cyclic (Lagrange's theorem).

[edit] Public-key cryptography

Main article: Public key cryptography

Several public-key cryptography algorithms, such as RSA or the Diffie-Hellman key exchange are based on large prime numbers (for example with 512 bits). They rely on the fact that it is much more easier (i.e., more efficient) to perform the multiplication of two (large) numbers x and y than to calculate x and y (assumed coprime) if only the product xy is known.

[edit] Prime numbers in nature

Inevitably, some of the numbers that occur in nature are prime. There are, however, relatively few examples of numbers that appear in nature because they are prime.

One example of the use of prime numbers in nature is as an evolutionary strategy used by cicadas of the genus Magicicada.[20] These insects spend most of their lives as grubs underground. They only pupate and then emerge from their burrows after 13 or 17 years, at which point they fly about, breed, and then die after a few weeks at most. The logic for this is believed to be that the prime number intervals between emergences makes it very difficult for predators to evolve that could specialise as predators on Magicicadas.[21] If Magicicadas appeared at a non-prime number intervals, say every 12 years, then predators appearing every 2, 3, 4, 6, or 12 years would be sure to meet them. Over a 200-year period, average predator populations during hypothetical outbreaks of 14- and 15-year cicadas would be up to 2% higher than during outbreaks of 13- and 17-year cicadas.[22] Though small, this advantage appears to have been enough to drive natural selection in favour of a prime-numbered life-cycle for these insects.

There is speculation that the zeros of the zeta function are connected to the energy levels of complex quantum systems.[23]

[edit] Generalizations

The concept of prime number is so important that it has been generalized in different ways in various branches of mathematics. Generally, "prime" indicates minimality or indecomposability, in an appropriate sense. For example, the prime field is the smallest subfield of a field F containing both 0 and 1. It is either Q or the finite field with p elements, whence the name. Often a second, additional meaning is intended by using the word prime, namely that any object can be, essentially uniquely, decomposed into its prime components. For example, in knot theory, a prime knot is a knot which is indecomposable in the sense that it cannot be written as the knot sum of two nontrivial knots. Any knot can be uniquely expressed as a connected sum of prime knots.[24] Prime models and prime 3-manifolds are other examples of this type.

[edit] Prime elements in rings

Prime numbers give rise to two more general concepts that apply to elements of any ring R, an algebraic structure where addition, subtraction and multiplication are defined: prime elements and irreducible elements. An element p of R is called prime if it is not a unit (i.e., does not have a multiplicative inverse) and the following property holds: given x and y in R such that p divides the product, then p divides at least one factor. Irreducible elements are ones which cannot be written as a product of two ring elements that are not units. In general, this is a weaker condition, but for any unique factorization domain, such as the ring Z of integers, the set of prime elements equals the set of irreducible elements, which for Z is {…, −11, −7, −5, −3, −2, 2, 3, 5, 7, 11, …}.

A common example are the Gaussian integers Z[i], that is, the set of complex numbers of the form a + bi with a and b in Z. This is an integral domain, its prime elements are known as Gaussian primes. Not every prime (in Z) is a Gaussian prime: in the bigger ring Z[i], 2 factors into the product of the two Gaussian primes (1 + i) and (1 − i). Rational primes (i.e. prime elements in Z) of the form 4k + 3 are Gaussian primes, whereas rational primes of the form 4k + 1 are not.

[edit] Prime ideals

Main article: Prime ideals

In ring theory, the notion of number is generally replaced with that of ideal. Prime ideals, which generalize prime elements in the sense that the principal ideal generated by a prime element is a prime ideal, are an important tool and object of study in commutative algebra, algebraic number theory and algebraic geometry. The prime ideals of the ring of integers are the ideals (0), (2), (3), (5), (7), (11), … The fundamental theorem of arithmetic generalizes to the Lasker-Noether theorem which expresses any ideal in a Noetherian commutative ring as the intersection of primary ideals, which are the appropriate generalizations of prime powers.

Prime ideals are the points of algebro-geometric objects, via the notion of the spectrum of a ring. Arithmetic geometry also benefits from this notion, and many concepts exist in both geometry and number theory. For example, the central problem in algebraic number theory, concerned with how a prime ideal factors or ramifies when it is lifted to an extension field, bears some resemblance with ramification in geometry.

[edit] Primes in valuation theory

In algebraic number theory, yet another generalization is used. A starting point for valuation theory is the p-adic valuations, where p is a prime number. It tells what highest power p divides a given number n. Using that, the p-adic norm is set up, which, in contrast to the usual absolute value, gets smaller when a number is multiplied by p. The completion of Q (the field of rational numbers) with respect to this norm leads to Qp, the field of p-adic numbers, as opposed to R, the reals, which are the completion with respect to the usual absolute value. In order to highlight the connection to primes, the absolute value is often called the infinite prime. These are essentially all possible ways to complete Q, by Ostrowski's theorem.

In an arbitrary field K, one considers valuations on K, certain functions from K to the real numbers R. Every such valuation yields a topology on K, and two valuations are called equivalent if they yield the same topology. A prime of K (sometimes called a place of K) is an equivalence class of valuations.

Arithmetic questions related to, global fields such as Q may, in certain cases, be transferred back and forth to the completed fields (known as local fields), a concept known as local-global principle. This again underlines the importance of primes to number theory.

[edit] In the arts and literature

Prime numbers have influenced many artists and writers. The French composer Olivier Messiaen used prime numbers to create ametrical music through "natural phenomena". In works such as La Nativité du Seigneur (1935) and Quatre études de rythme (1949-50), he simultaneously employs motifs with lengths given by different prime numbers to create unpredictable rhythms: the primes 41, 43, 47 and 53 appear in one of the études. According to Messiaen this way of composing was "inspired by the movements of nature, movements of free and unequal durations". [25]

In his science fiction novel Contact, later made into a film of the same name, the NASA scientist Carl Sagan suggested that prime numbers could be used as a means of communicating with aliens, an idea that he had first developed informally with American astronomer Frank Drake in 1975. [26]

Tom Stoppard's 1993 play Arcadia was a conscious attempt to discuss mathematical ideas on the stage. In the opening scene, the 13 year old heroine puzzles over Fermat's Last Theorem, a theorem involving prime numbers.[27][28] Many films reflect a popular fascination with the mysteries of prime numbers and cryptography: films such as Cube, Sneakers, The Mirror Has Two Faces and A Beautiful Mind, the latter of which is based on the biography of the mathematician and Nobel laureate John Forbes Nash by Sylvia Nasar.[29] [30] In the novel PopCo by Scarlett Thomas the main character, Alice Butler's grandmother works on proving the Riemann Hypothesis. In the book, a table of the first 1000 prime numbers is displayed.[31]

[edit] See also

[edit] Distributed computing projects that search for primes

[edit] Notes

  1. ^ Riesel 1994, p. 36.
  2. ^ Conway & Guy 1996, pp. 129–130.
  3. ^ Gowers 2002, p. 118 "The seemingly arbitrary exclusion of 1 from the definition of a prime … does not express some deep fact about numbers: it just happens to be a useful convention, adopted so there is only one way of factorizing any given number into primes."
  4. ^ ""Why is the number one not prime?"". Retrieved 2007-10-02.
  5. ^ ""Arguments for and against the primality of 1".
  6. ^ The Largest Known Prime by Year: A Brief History Prime Curios!: 17014…05727 (39-digits)
  7. ^ Hardy 1908, pp. 122–123.
  8. ^ Letter in Latin from Goldbach to Euler, July 1730.
  9. ^ Ribenboim 2004, p. 4.
  10. ^ Furstenberg 1955.
  11. ^ The Top Twenty: Primorial
  12. ^ The Top Twenty: Factorial
  13. ^ The Top Twenty: Twin Prime Search
  14. ^ Havil 2003, p. 163.
  15. ^ Havil 2003, p. 171.
  16. ^ Eric W. Weisstein, Landau's Problems at MathWorld.
  17. ^ Caldwell, Chris, The Top Twenty: Lucas Number at The Prime Pages.
  18. ^ E.g., see Guy 1981, problem A3, pp. 7–8.
  19. ^ Hardy 1940 "No one has yet discovered any warlike purpose to be served by the theory of numbers or relativity, and it seems unlikely that anyone will do so for many years."
  20. ^ Goles, E., Schulz, O. and M. Markus (2001). "Prime number selection of cycles in a predator-prey model", Complexity 6(4): 33-38
  21. ^ Paulo R. A. Campos, Viviane M. de Oliveira, Ronaldo Giro, and Douglas S. Galvão. (2004). "Emergence of Prime Numbers as the Result of Evolutionary Strategy". Phys. Rev. Lett. 93: 098107. doi:10.1103/PhysRevLett.93.098107. http://link.aps.org/abstract/PRL/v93/e098107. Retrieved on 2006-11-26. 
  22. ^ "Invasion of the Brood". The Economist. May 6, 2004. http://economist.com/PrinterFriendly.cfm?Story_ID=2647052. Retrieved on 2006-11-26. 
  23. ^ Ivars Peterson (June 28, 1999). "The Return of Zeta". MAA Online. http://www.maa.org/mathland/mathtrek_6_28_99.html. Retrieved on 2008-03-14. 
  24. ^ Schubert, H. "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten". S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), 57–104.
  25. ^ Hill, ed. 1995.
  26. ^ Carl Pomerance, Prime Numbers and the Search for Extraterrestrial Intelligence, Retrieved on December 22, 2007
  27. ^ Stoppard 1993.
  28. ^ Kelly, ed. 2001.
  29. ^ Music of the Spheres, Marcus du Sautoy's selection of films featuring prime numbers
  30. ^ A Beautiful Mind
  31. ^ - A Mathematician reviews PopCo

[edit] References

[edit] Further references

[edit] External links

Sister project Wikinews has related news: Two largest known prime numbers discovered just two weeks apart, one qualifies for $100k prize

[edit] Prime number generators & calculators

Retrieved from "http://en.wikipedia.org/wiki/Prime_number"
Personal tools