Log-normal distribution

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Log-normal
Probability density function
Plot of the Lognormal PMF
μ=0
Cumulative distribution function
Plot of the Lognormal CMF
μ=0
Parameters σ > 0
-\infty < \mu < \infty
Support [0,+\infty)\!
Probability density function (pdf) \frac{1}{x\sigma\sqrt{2\pi}}\exp\left[-\frac{\left(\ln(x)-\mu\right)^2}{2\sigma^2}\right]
Cumulative distribution function (cdf) \frac{1}{2}+\frac{1}{2} \mathrm{erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]
Mean e^{\mu+\sigma^2/2}
Median e^{\mu}\,
Mode e^{\mu-\sigma^2}
Variance (e^{\sigma^2}\!\!-1) e^{2\mu+\sigma^2}
Skewness (e^{\sigma^2}\!\!+2)\sqrt{e^{\sigma^2}\!\!-1}
Excess kurtosis {e^{4\sigma^2}+2e^{3\sigma^2}+3e^{2\sigma^2}-6}
Entropy \frac{1}{2}+\frac{1}{2}\ln(2\pi\sigma^2) + \mu
Moment-generating function (mgf) (see text for raw moments)
Characteristic function needs your contribution

In probability and statistics, the log-normal distribution is the single-tailed probability distribution of any random variable whose logarithm is normally distributed. If X is a random variable with a normal distribution, then Y = exp(X) has a log-normal distribution; likewise, if Y is log-normally distributed, then log(Y) is normally distributed. (The base of the logarithmic function does not matter: if loga(Y) is normally distributed, then so is logb(Y), for any two positive numbers a, b ≠ 1.)

Log-normal is also written log normal or lognormal.

A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many independent random variables each of which is positive. For example, in finance, a long-term discount factor can be derived from the product of short-term discount factors. In wireless communication, the attenuation caused by shadowing or slow fading from random objects is often assumed to be log-normally distributed. See log-distance path loss model‎.

Contents

[edit] Characterization

[edit] Probability density function

The log-normal distribution has the probability density function

f(x;\mu,\sigma) = \frac{1}{x \sigma \sqrt{2 \pi}}e^{-\frac{(\ln (x) - \mu)^2}{2\sigma^2}}

for x > 0, where μ and σ are the mean and standard deviation of the variable's natural logarithm (by definition, the variable's logarithm is normally distributed).

[edit] Cumulative distribution function

\frac{1}{2}+\frac{1}{2} \mathrm{erf}\left[\frac{\ln(x)-\mu}{\sigma\sqrt{2}}\right]

[edit] Properties

[edit] Mean and standard deviation

If X is a lognormally distributed variable, its expected value (mean) is

\mathrm{E}(X) = e^{\mu + \sigma^2/2}\,\!

and its variance is

\mathrm{Var}(X) = (e^{\sigma^2} - 1) e^{2\mu + \sigma^2}\,\!

hence the standard deviation is

\mathrm{Std Dev}(X) = \sqrt{\mathrm{Var}(X)} = e^{\mu + \sigma^2/2}\sqrt{(e^{\sigma^2} - 1)}\,\!

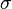Equivalent relationships may be written to obtain \mu\,\! and \sigma\,\! given the expected value and variance:

\mu = \ln(\mathrm{E}(X))-\frac{1}{2}\ln\left(1+\frac{\mathrm{Var}(X)}{(\mathrm{E}(X))^2}\right)\,\!
\sigma^2 = \ln\left(\frac{\mathrm{Var}(X)}{(\mathrm{E}(X))^2}+1\right)\,\!

[edit] Mode and median

The mode is

\mathrm{Mode}(X) = e^{\mu - \sigma^2}\,\!

The median is

\tilde{X} = e^{\mu}\,\!

[edit] Geometric mean and geometric standard deviation

The geometric mean of the log-normal distribution is e^{\mu}\,\!, and the geometric standard deviation is equal to e^{\sigma}\,\!.

If a sample of data is determined to come from a log-normally distributed population, the geometric mean and the geometric standard deviation may be used to estimate confidence intervals akin to the way the arithmetic mean and standard deviation are used to estimate confidence intervals for a normally distributed sample of data.

Confidence interval bounds log space geometric
3σ lower bound \mu - 3\sigma\,\! \mu_\mathrm{geo} / \sigma_\mathrm{geo}^3\,\!
2σ lower bound \mu - 2\sigma\,\! \mu_\mathrm{geo} / \sigma_\mathrm{geo}^2\,\!
1σ lower bound \mu - \sigma\,\! \mu_\mathrm{geo} / \sigma_\mathrm{geo}\,\!
1σ upper bound \mu + \sigma\,\! \mu_\mathrm{geo} \sigma_\mathrm{geo}\,\!
2σ upper bound \mu + 2\sigma\,\! \mu_\mathrm{geo} \sigma_\mathrm{geo}^2\,\!
3σ upper bound \mu + 3\sigma\,\! \mu_\mathrm{geo} \sigma_\mathrm{geo}^3\,\!

Where geometric mean \mu_\mathrm{geo} = \exp(\mu)\,\! and geometric standard deviation \sigma_\mathrm{geo} = \exp(\sigma)\,\!

[edit] Moments

For any real number s, the sth moment is given by

\operatorname{E}(X^s)=e^{s\mu+s^2\sigma^2/2}.

A log-normal distribution is not uniquely determined by its moments E(Xk) for k ≥ 1, that is, there exists some other distribution with the same moments for all k.

[edit] Moment generating function

The moment-generating function for the log-normal distribution does not exist on the domain R, but the moment generating function does exist on (−∞, 0]. The set {t : g(t) < ∞}, where g is the moment-generating function, contains (−∞, 0].

[edit] Partial expectation

The partial expectation of a random variable X with respect to a threshold k is defined as

g(k)=\int_k^\infty x f(x)\, dx\,\!

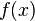where f(x)\,\! is the density. For a lognormal density it can be shown that

g(k)=\exp(\mu+\sigma^2/2)\Phi\left(\frac{-\ln(k)+\mu+\sigma^2}{\sigma}\right)\,\!

where \scriptstyle\Phi\,\! is the cumulative distribution function of the standard normal. The partial expectation of a lognormal has applications in insurance and in economics (for example it can be used to derive the Black–Scholes formula).

[edit] Maximum likelihood estimation of parameters

For determining the maximum likelihood estimators of the log-normal distribution parameters μ and σ, we can use the same procedure as for the normal distribution. To avoid repetition, we observe that

f_L (x;\mu, \sigma) = \frac 1 x \, f_N (\ln x; \mu, \sigma)

where by ƒL we denote the probability density function of the log-normal distribution and by ƒN that of the normal distribution. Therefore, using the same indices to denote distributions, we can write the log-likelihood function thus:

\begin{align} \ell_L (\mu,\sigma | x_1, x_2, \dots, x_n) & {} = - \sum _k \ln x_k + \ell_N (\mu, \sigma | \ln x_1, \ln x_2, \dots, \ln x_n) \\ & {} = \operatorname {constant} + \ell_N (\mu, \sigma | \ln x_1, \ln x_2, \dots, \ln x_n). \end{align}

Since the first term is constant with regard to μ and σ, both logarithmic likelihood functions, \ell_L and \ell_N, reach their maximum with the same μ and σ. Hence, using the formulas for the normal distribution maximum likelihood parameter estimators and the equality above, we deduce that for the log-normal distribution it holds that

\widehat \mu = \frac {\sum_k \ln x_k} n, \ \widehat \sigma^2 = \frac {\sum_k {\left( \ln x_k - \widehat \mu \right)^2}} {n}.


[edit] Generating Log-normally-distributed random variates

Given a random variate N drawn from the normal distribution with 0 mean and 1 standard deviation, then the variate

X= e^{\mu + \sigma N}\,

has a Log-normal distribution with parameters μ and σ.

[edit] Related distributions

  • If 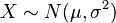X \sim N(\mu, \sigma^2) is a normal distribution then \exp(X) \sim \operatorname{Log-N}(\mu, \sigma^2).
  • If Y \sim \operatorname{Log-N}(\mu, \sigma^2) is a log-normally distributed random variable then ln(Y)˜N(μ,σ2) is a normally distributed random variable.
  • If X_m \sim \operatorname {Log-N} (\mu, \sigma_m^2), \ m = 1,\dots, n are independent log-normally distributed variables with the same μ parameter and possibly varying σ, and Y = \prod_{m=1}^n X_m, then Y is a log-normally distributed variable as well:
Y \sim \operatorname {Log-N} \left( n\mu, \sum _{m=1}^n \sigma_m^2 \right).
  • Let X_m \sim \operatorname {Log-N} (\mu_m,\sigma_m^2), \ m={1,\dots,n} \ be independent log-normally distributed variables with

possibly varying σ and μ parameters, and Y=\sum_{m=1}^n X_m. The distribution of Y has no closed-form expression, but can be reasonably approximated by another log-normal distribution Z at the right tail. Its probability density function at the neighborhood of 0 is characterized in (Gao et al., 2009) and it does not resemble any log-normal distribution. A commonly used approximation (due to Fenton and Wilkinson) is obtained by matching the mean and variance:

\sigma^2_Z = \log\left[ \frac{\sum e^{2\mu_m+\sigma_m^2}(e^{\sigma_m^2}-1)}{(\sum e^{\mu_m+\sigma_m^2/2})^2}+1\right]
\mu_Z = \log\left( \sum e^{\mu_m+\sigma_m^2/2} \right)- \frac{\sigma^2_Z}{2}.

In the case that all Xm have the same variance parameter σm = σ, these formulas simplify to

\sigma^2_Z = \log\left[ (e^{\sigma^2}-1)\frac{\sum e^{2\mu_m}}{(\sum e^{\mu_m})^2}+1\right]
\mu_Z = \log\left( \sum e^{\mu_m} \right) + \frac{\sigma^2}{2} - \frac{\sigma^2_Z}{2}.
  • A substitute for the log-normal whose integral can be expressed in terms of more elementary functions (Swamee, 2002) can be obtained based on the logistic distribution to get the CDF
F(x;\mu,\sigma) = \left[\left(\frac{e^\mu}{x}\right)^{\pi/(\sigma \sqrt{3})} +1\right]^{-1}.

This is a log-logistic distribution.

  • If X \sim \operatorname {Log-N} (\mu, \sigma^2) then X + c is called shifted log-normal.

[edit] Further reading

[edit] References

[edit] See also

v • d • e
Probability distributions
 
Continuous univariate supported on a semi-infinite interval, usually [0,∞)
Retrieved from "http://en.wikipedia.org/wiki/Log-normal_distribution"
Personal tools