Isometric projection

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Part of a series on:
Graphical projection
v • d • e

Isometric projection is a form of graphical projection, more specifically, a form of axonometric projection. It is a method of visually representing three-dimensional objects in two dimensions, in which the three coordinate axes appear equally foreshortened and the angles between any two of them are 120°.

Isometric projection is one of the projections used in technical and engineering drawings.

Contents

[edit] Overview

The term "isometric" comes from the Greek for "equal measure", reflecting that the scale along each axis of the projection is the same (this is not true of some other forms of graphical projection).

Isometric drawing of a cube.

An isometric view of an object can be obtained by choosing the viewing direction in a way that the angles between the projection of the x, y, and z axes are all the same, or 120°. For example when taking a cube, this is done by first looking straight towards one face. Next the cube is rotated ±45° about the vertical axis, followed by a rotation of approximately ±35.264° (precisely arcsin(tan 30°) ) about the horizontal axis. Note that with the cube (see image) the perimeter of the 2D drawing is a perfect regular hexagon: all the black lines are of equal length and all the cube's faces are the same area.

In a similar way an isometric view can be obtained for example in a 3D scene editor. Starting with the camera aligned parallel to the floor and aligned to the coordinate axes, it is first rotated downwards around the horizontal axes by about 35.264° as above, and then rotated ±45° around the vertical axes.

Another way in which isometric projection can be visualized is by considering a view within a cubical room starting in an upper corner and looking towards the opposite, lower corner. The x-axis extends diagonally down and right, the y-axis extends diagonally down and left, and the z-axis is straight up. Depth is also shown by height on the image. Lines drawn along the axes are at 120° to one another.

[edit] Mathematics

There are 8 different orientations to obtain an isometric view, depending into which octant the viewer looks. The isometric transform from a point ax,y,z in 3D space to a point bx,y in 2D space looking into the first octant can be written mathematically with rotation matrices as:

\begin{bmatrix} \mathbf{c}_x \\ \mathbf{c}_y \\ \mathbf{c}_z \\ \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & {\cos\alpha} & {\sin\alpha} \\ 0 & { - \sin\alpha} & {\cos\alpha} \\ \end{bmatrix}\begin{bmatrix} {\cos\beta } & 0 & { - \sin\beta } \\ 0 & 1 & 0 \\ {\sin\beta } & 0 & {\cos\beta } \\ \end{bmatrix}\begin{bmatrix} \mathbf{a}_x \\ \mathbf{a}_y \\ \mathbf{a}_z \\ \end{bmatrix}=\frac{1}{\sqrt{6}}\begin{bmatrix} \sqrt{3} & 0 & -\sqrt{3} \\ 1 & 2 & 1 \\ \sqrt{2} & -\sqrt{2} & \sqrt{2} \\ \end{bmatrix}\begin{bmatrix} \mathbf{a}_x \\ \mathbf{a}_y \\ \mathbf{a}_z \\ \end{bmatrix}

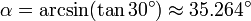where \alpha = \arcsin(\tan30^\circ)\approx35.264^\circ and \beta = 45^\circ. As explained above, this is a rotation around the vertical (here y) axis by β, followed by a rotation around the horizontal (here x) axis by α. This is then followed by an orthographic projection to the x-y plane:

\begin{bmatrix} \mathbf{b}_x \\ \mathbf{b}_y \\ 0 \\ \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\begin{bmatrix} \mathbf{c}_x \\ \mathbf{c}_y \\ \mathbf{c}_z \\ \end{bmatrix}

The other seven possibilities are obtained by either rotating to the opposite sides or not, and then inverting the view direction or not.[1]

[edit] Limits of axonometric projection

Example of limitations

As with all types of parallel projection, objects drawn with axonometric projection do not appear larger or smaller as they extend closer to or away from the viewer. While advantageous for architectural drawings, this results in a perceived distortion, as unlike perspective projection, it is not how our eyes or photography normally work. It also can easily result in situations where depth and altitude are difficult to gauge, as is shown in the illustration to the right.

Once popular in sprite-based video games, most contemporary video games have avoided these sorts of situations by switching over to perspective 3D instead.

Such illusions were also popular in Op art such as M. C. Escher's "impossible architecture" drawings. Waterfall (1961), in which the drawing of the building makes use of axonometric projection, but the faded background uses perspective projection, is a well-known example. Another advantage is that, in engineering drawings, 60° angles are easier for novices to construct using only a compass and straightedge.

In this isometric drawing for example, the blue sphere is two levels higher than the red one. However, this difference in elevation is not apparent if one covers the right half of the picture, as the boxes (which serve as clues suggesting height) are then obscured.

[edit] Isometric projection in video games and pixel art

A television set drawn in near- isometric pixel art.[2]

In the fields of computer and video games and pixel art, axonometric projection has been popular because of the ease with which 2D sprites and tile-based graphics can be made to represent a 3D gaming environment. Because objects do not change size as they move about the game field, there is no need for the computer to scale sprites or do the calculations necessary to simulate visual perspective. This allowed older 8-bit and 16-bit game systems (and, more recently, handheld systems) to portray large 3D areas easily. While the depth confusion problems illustrated above can sometimes be a problem, good game design can alleviate this. With the advent of more powerful graphics systems, axonometric projection is becoming less common.

Corresponding camera rotations for true isometric projection (at left) and the form of dimetric perspective commonly found in video games and pixel art (at right).[3]

The projection used in videogames usually deviates slightly from "true" isometric due to the limitations of raster graphics. Lines in the x and y directions would not follow a neat pixel pattern if drawn in the required 30° to the horizontal. While modern computers can eliminate this problem using anti-aliasing, earlier computer graphics did not support enough colors or possess enough CPU power to accomplish this. So instead, a 2:1 pixel pattern ratio would be used to draw the x and y axis lines, resulting in these axes following a 26.565° (arctan 0.5) angle to the horizontal. (Game systems that do not use square pixels could, however, yield different angles, including true isometric.) Therefore, this form of projection is more accurately described as a variation of dimetric projection, since only two of the three angles between the axes are equal (116.565°, 116.565°, 126.87°). Many in video game and pixel art communities, however, continue to colloquially refer to this projection as "isometric perspective"; the terms "3/4 perspective" and "2.5D" are also commonly used.

The term has also been applied to games that do not use the 2:1 pixel pattern ratio, including Fallout[4] and SimCity 4[5] (which use trimetric projection); The Legend of Zelda: A Link to the Past[6] and Ultima Online[7] (which use oblique projection); and The Age of Decadence[8] and Silent Storm[9] (which use perspective projection and a bird's eye view).

[edit] History of isometric video games

Q*bert from 1982 was one of the first games to use isometric graphics.
For a comprehensive list of isometric video games, see Category:Video games with isometric graphics‎.

While the history of computer games saw some true 3D games as soon as the early 1970s, the first video games to use the distinct visual style of isometric projection in the meaning described above were arcade games in the early 1980s.

Q*bert[10] and Zaxxon[11] were both released in 1982. Q*bert showed a static pyramid drawn in an isometric perspective, with the player controlling a person which could jump around on the pyramid. Zaxxon employed scrolling isometric levels where the player controlled a plane to fly through the levels. A year later in 1983 the arcade game Congo Bongo was released, running on the same hardware as Zaxxon[12]. It allowed the player character to move around in bigger isometric levels, including true three-dimensional climbing and falling. The same was possible in the 1984 arcade title Marble Madness.

Knight Lore from 1984 is considered to first define the genre of isometric adventure games.

At this time, isometric games were no longer exclusive to the arcade market and also entered home computers with the release of Ant Attack for the ZX Spectrum in 1983. The player could now move forward in any direction of the scrolling game, offering complete free movement rather than fixed to one axis as with Zaxxon. The views could also be changed around a 90 degrees axis. [13] The ZX Crash magazine consequently awarded it 100% in the graphics category for this new technique, known as "Soft Solid 3-D".[14]

A year later the ZX saw the release of Knight Lore, which is generally regarded as a revolutionary title[15] that defined the subsequent genre of isometric adventure games.[16] Following Knight Lore, many isometric titles were seen on home computers - to an extent that it once was regarded as being the second most cloned piece of software after WordStar.[17] One big success out of those was the 1987 game Head Over Heels.[18] Isometric perspective was not limited to arcade/adventure games, though; for example, the 1989 strategy game Populous used isometric perspective.

Throughout the 1990s some very successful games like Civilization II and Diablo used a fixed isometric perspective. But with the advent of 3D acceleration on personal computers and gaming consoles, games using a 3D perspective generally started using true 3D instead of isometric perspective. This can be seen by successors of the above games; starting with Civilization IV, the Civilization series uses full 3D. Diablo II used a fixed perspective like its predecessor, but optionally allowed for perspective scaling of the sprites in the distance to lend a pseudo-3D perspective.[19]

[edit] See also

[edit] References

  1. ^ Ingrid Carlbom, Joseph Paciorek (December 1978). "Planar Geometric Projections and Viewing Transformations". ACM Computing Surveys (CSUR) (ACM) 10 (4): 465–502. doi:10.1145/356744.356750. ISSN 0360-0300. 
  2. ^ Note the 2:1 pixel pattern ratio in this blown-up image
  3. ^ Note: the blue vectors point towards the camera positions. The red arcs represent the rotations around the horizontal and vertical axes. The white box matches the one shown in the image at the top of the article.
  4. ^ Green, Jeff (2000-02-29). "GameSpot Preview: Arcanum" (HTML). GameSpot. CNET Networks, Inc. http://www.gamespot.com/features/arcanum_pre/. Retrieved on 2008-01-10. 
  5. ^ Butts, Steve (2003-09-09). "SimCity 4: Rush Hour Preview" (HTML). IGN PC. IGN Entertainment, Inc. http://pc.ign.com/articles/437/437280p1.html. Retrieved on 2008-01-10. 
  6. ^ "GDC 2004: The History of Zelda" (HTML). IGN GameCube. IGN Entertainment, Inc. 2004-03-25. http://cube.ign.com/articles/501/501970p1.html. Retrieved on 2007-12-17. 
  7. ^ Greely, Dave; Ben Sawyer (1997-08-19A). "Has Origin Created the First True Online Game World?" (HTML). Gamasutra. CMP Media LLC. http://www.gamasutra.com/features/19970819/sawyer_01.htm. Retrieved on 2007-12-17. 
  8. ^ "Age of Decadence" (HTML). Iron Tower Studios. http://www.irontowerstudio.com/index.htm. Retrieved on 2007-07-10. 
  9. ^ O'Hagan, Steve (2008-08-07). "PC Previews: Silent Storm" (HTML). ComputerAndVideoGames.com. Future Publishing Limited. http://www.computerandvideogames.com/article.php?id=94816. Retrieved on 2007-12-13. 
  10. ^ Q*bert at the Killer List of Videogames
  11. ^ Zaxxon at the Killer List of Videogames
  12. ^ Congo Bongo at the Killer List of Videogames
  13. ^ "Sculptin the new shape of Spectrum games". Sinclair User (21). December 1983. http://www.worldofspectrum.org/showmag.cgi?mag=SinclairUser/Issue021/Pages/SinclairUser02100088.jpg. Retrieved on 2009-03-02. 
  14. ^ "Soft Solid 3D Ant Attack". CRASH (1). February 1984. http://www.crashonline.org.uk/01/antattack.htm. Retrieved on 2008-09-29. 
  15. ^ "Ultimate Play The Game—Company Lookback". Retro Micro Games Action - The Best of gamesTM Retro Volume 1. Highbury Entertainment. 2006. p. 25. 
  16. ^ Steven Collins. "Game Graphics During the 8-bit Computer Era". Computer Graphics Newsletters. SIGGRAPH. http://www.siggraph.org/publications/newsletter/v32n2/contributions/collins.html. Retrieved on 2007-08-16. 
  17. ^ Krikke, J. (Jul/August 2000). "Axonometry: a matter of perspective". Computer Graphics and Applications (IEEE) 20 (4): 7–11. doi:10.1109/38.851742. 
  18. ^ "Looking for an old angle". CRASH (51). April 1988. http://www.crashonline.org.uk/51/runagain.htm. Retrieved on 2008-09-29. 
  19. ^ "Diablo II Nears Completion As Blizzard Prepares For Final Phase Of Beta Testing". FindArticles. Marketwire (BNET Business Network). May 2000. http://findarticles.com/p/articles/mi_pwwi/is_200005/ai_mark15009744. Retrieved on 2008-09-29. 
 This article needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (March 2009)

[edit] External links

Sister project Wikimedia Commons has media related to: Isometric projection
Retrieved from "http://en.wikipedia.org/wiki/Isometric_projection"
Personal tools