Natural units

From Wikipedia, the free encyclopedia

In physics, natural units are physical units of measurement defined in such a way that certain selected universal physical constants are normalized to unity; that is, their numerical value becomes exactly 1 when measured in some system of natural units.

1 Introduction
2 Candidate physical constants used in natural unit systems
3 Planck units
4 Stoney units
5 "Schrödinger" units
6 Atomic units (Hartree)
7 Electronic system of units
8 Quantum chromodynamical system of units (Strong)
9 Geometrized units
10 N-body units
11 See also
12 References
13 External links

[edit] Introduction

Natural units are intended to elegantly simplify particular algebraic expressions appearing in physical law or to normalize some chosen physical quantities that are properties of universal elementary particles and that may be reasonably believed to be constant. However, what may be believed and forced to be constant in one system of natural units can very well be allowed or even assumed to vary in another natural unit system.

Natural units are natural because the origin of their definition comes only from properties of nature and not from any human construct. Planck units are often, without qualification, called "natural units," when in fact they are only one of several systems of natural units, albeit the best known such system. Planck units might be considered unique in that the set of units are not based on properties of any prototype, object, or particle but are solely derived from the properties of free space.

As with any set of base units or fundamental units the base units of a set of natural units will include definitions and values for length, mass, time, temperature, and electric charge. Some physicists do not recognize temperature as a fundamental physical quantity, since it simply expresses the energy per degree of freedom of a particle, which can be expressed in terms of energy (or mass, length, and time). Virtually every system of natural units normalizes the Boltzmann constant to k=1, which can be thought of as simply a way of defining the unit temperature.

In addition, some physicists recognize electric charge as a separate fundamental dimension of physical quantity, even if it has been expressed in terms of mass, length, and time in unit systems such as the electrostatic cgs system. Virtually every system of natural units normalizes the permittivity of free space to ε₀=(4π)^-1, an expression which can be thought of as defining the unit charge. This suggests that the controversial^[1] adoption, first in CGS units and subsequently in SI units, of Georgi's preference for expressing Coulomb's law in the "rationalized" form F= (4πε₀)^-1q₁q₂r^-2, rather than as F=kq₁q₂r^-2, may not have been the most natural choice after all.

[edit] Candidate physical constants used in natural unit systems

The candidate physical constants to be normalized are chosen from those in the following table. Note that only a smaller subset of the following can be normalized in any one system of units without contradiction in definition (e.g., m_e and m_p cannot both be defined as the unit mass in a single system).

Constant	Symbol	Dimension
speed of light in vacuum	${ c } \$	L T^-1
Gravitational constant	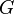${ G } \$	M^-1L³T^-2
Planck's constant (reduced)	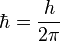$\hbar=\frac{h}{2 \pi}$	ML²T^-1
Coulomb force constant	$\frac{1}{4 \pi \epsilon_0}$ where ${ \epsilon_0 } \$ is the permittivity of free space	Q^-2 M L³ T^-2
Elementary charge	$e \$	Q
Electron mass	$m_e \$	M
Proton mass	$m_p \$	M
Boltzmann constant	${ k } \$	ML²T^-2Θ^-1

Dimensionless physical constants such as the fine-structure constant

$\alpha \ \equiv \frac{e^2}{\hbar c (4 \pi \epsilon_0)} = \frac{1}{137.03599911}$

cannot take on a different numerical value no matter what system of units is used. Judiciously choosing units can only normalize physical constants that have dimension. Since α is a fixed dimensionless number not equal to 1, it is not possible to define a system of natural units that will normalize all of the physical constants that comprise α. Any 3 of the 4 constants: c, 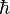$\hbar$ , e, or 4πε₀, can be normalized (leaving the remaining physical constant to take on a value that is a simple function of α, attesting to the fundamental nature of the fine-structure constant) but not all 4.

[edit] Planck units

Main article: Planck units

Quantity	Expression	Metric value
Length (L)	$l_P = \sqrt{\frac{\hbar G}{c^3}}$	1.61609735×10^-35 m
Mass (M)	$m_P = \sqrt{\frac{\hbar c}{G}}$	21.7664598 μg
Time (T)	$t_P = \sqrt{\frac{\hbar G}{c^5}}$	5.3907205×10^-44 s
Electric charge (Q)	$q_P = \sqrt{\hbar c (4 \pi \epsilon_0)}$	1.87554573×10^-18 C
Temperature (Θ)	$T_P = \sqrt{\frac{\hbar c^5}{G k^2}}$	1.4169206×10³² K

$c = 1 \$

$G = 1 \$

$\hbar = 1 \$

$\frac{1}{4 \pi \epsilon_0} = 1$

$k = 1 \$

$e = \sqrt{\alpha} \$

Planck units hold pride of place among systems of natural units, because they do not invoke any properties (specifically, the charge, mass, or orbital radius) of any elementary particle. For example, the proton and electron are equally sensible choices, and thus are equally arbitrary. But their masses differ considerably, a fact having nontrivial implications for all other systems of natural units, because these all invoke one or more properties of protons or electrons.

By contrast, the physical constants that Planck units normalize are all properties of free space. In particular, the definition of Planck units does not invoke the elementary charge, whose numerical value, when measured in units of Planck charge, is the square root of the fine-structure constant α. Hence any observed variation over space or time in the value of α is attributed to variation in the elementary charge.

[edit] Stoney units

Quantity	Expression	Metric Value
Length (L)	$l_S = \sqrt{\frac{G e^2}{c^4 (4 \pi \epsilon_0)}}$	1.38068×10^-36 m
Mass (M)	$m_S = \sqrt{\frac{e^2}{G (4 \pi \epsilon_0)}}$	1.85921×10^-9 kg
Time (T)	$t_S = \sqrt{\frac{G e^2}{c^6 (4 \pi \epsilon_0)}}$	4.60544×10^-45 s
Electric charge (Q)	$q_S = e \$	1.60218×10^-19 C
Temperature (Θ)	$T_S = \sqrt{\frac{c^4 e^2}{G (4 \pi \epsilon_0) k^2}}$	1.21028×10³¹ K

$c = 1 \$

$G = 1 \$

$e = 1 \$

$\frac{1}{4 \pi \epsilon_0} = 1$

$k = 1 \$

$\hbar = \frac{1}{\alpha} \$

George Johnstone Stoney was the first physicist to introduce the concept of natural units. He presented the idea in a lecture entitled "On the Physical Units of Nature" delivered to the British Association in 1874.^[2] Stoney units fix the elementary charge and allow Planck's constant (only discovered after Stoney's proposal) to float. They can be obtained from Planck units with the substitution:

$\hbar \leftarrow \alpha \hbar = \frac{e^2}{c (4 \pi \epsilon_0)}$ .

This removes Planck's constant from the definitions and the value it takes on in Stoney units is the reciprocal of the fine-structure constant, 1/α. Hence any observed variation over space or time in the value of α is attributed to variation in Planck's constant.

[edit] "Schrödinger" units

Quantity	Expression	Metric Value
Length (L)	$l_{\psi} = \sqrt{\frac{\hbar^4 G (4 \pi \epsilon_0)^3}{e^6}}$	2.59276×10^-32 m
Mass (M)	$m_{\psi} = \sqrt{\frac{e^2}{G (4 \pi \epsilon_0)}}$	1.85921×10^-9 kg
Time (T)	$t_{\psi} = \sqrt{\frac{\hbar^6 G (4 \pi \epsilon_0)^5}{e^{10}}}$	1.18516×10^-38 s
Electric charge (Q)	$q_{\psi} = e \$	1.602176487×10^-19 C
Temperature (Θ)	$T_{\psi} = \sqrt{\frac{e^{10}}{\hbar^4 (4 \pi \epsilon_0)^5 G k^2}}$	6.44490×10²⁶ K

$e = 1 \$

$G = 1 \$

$\hbar = 1 \$

$\frac{1}{4 \pi \epsilon_0} = 1$

$k = 1 \$

$c = \frac{1}{\alpha} \$

The name was coined by Michael Duff [1]. They can be obtained from Planck units with the substitution:

$c \leftarrow \alpha c = \frac{e^2}{\hbar (4 \pi \epsilon_0)}$ .

This removes the speed of light from the definitions and the value it takes on in Schrödinger units is the reciprocal of the fine-structure constant, 1/α. Hence any observed variation over space or time in the value of α is attributed to variation in the speed of light,

[edit] Atomic units (Hartree)

Main article: Atomic units

Quantity	Expression
Length (L)	$l_A = \frac{\hbar^2 (4 \pi \epsilon_0)}{m_e e^2}$
Mass (M)	$m_A = m_e \$
Time (T)	$t_A = \frac{\hbar^3 (4 \pi \epsilon_0)^2}{m_e e^4}$
Electric charge (Q)	$q_A = e \$
Temperature (Θ)	$T_A = \frac{m_e e^4}{\hbar^2 (4 \pi \epsilon_0)^2 k}$

$e = 1 \$

$m_e = 1 \$

$\hbar = 1 \$

$\frac{1}{4 \pi \epsilon_0} = 1$

$k = 1 \$

$c = \frac{1}{\alpha} \$

First proposed by Douglas Hartree to simplify the physics of the Hydrogen atom. Michael Duff [2] calls these "Bohr units". The unit energy in this system is the total energy of the electron in the first circular orbit of the Bohr atom and called the Hartree energy, E_h. The unit velocity is the velocity of that electron, the unit mass is the electron mass, m_e, and the unit length is the Bohr radius, $a_0 = 4 \pi \epsilon_0\hbar^2/m_e e^2 \$ . They can be obtained from "Schrödinger" units with the substitution:

$G \leftarrow \alpha G \left( \frac{m_P}{m_e} \right)^2 = \frac{e^2}{4 \pi \epsilon_0 m_e^2} \$ .

This removes the speed of light (as well as the gravitational constant) from the definitions and its numerical value in atomic units is the reciprocal of the fine-structure constant, 1/α. Hence any observed variation over space or time in the value of α is attributed to variation in the speed of light.

[edit] Electronic system of units

Quantity	Expression
Length (L)	$l_e = \frac{e^2}{c^2 m_e (4 \pi \epsilon_0)}$
Mass (M)	$m_e = m_e \$
Time (T)	$t_e = \frac{e^2}{c^3 m_e (4 \pi \epsilon_0)}$
Electric charge (Q)	$q_e = e \$
Temperature (Θ)	$T_e = \frac{m_e c^2}{k}$

$c = 1 \$

$e = 1 \$

$m_e = 1 \$

$\frac{1}{4 \pi \epsilon_0} = 1$

$k = 1 \$

$\hbar = \frac{1}{\alpha} \$

Michael Duff [3] calls these "Dirac units". They can be obtained from Stoney units via the substitution:

$G \leftarrow \alpha G \left( \frac{m_P}{m_e} \right)^2 = \frac{e^2}{4 \pi \epsilon_0 m_e^2} \$ .

They can be also obtained from atomic units with the substitution:

$\hbar \leftarrow \alpha \hbar = \frac{e^2}{c (4 \pi \epsilon_0)}$ .

As is the case with Stoney units, any observed variation over space or time in the value of α is attributed to variation in Planck's constant.

[edit] Quantum chromodynamical system of units (Strong)

Quantity	Expression
Length (L)	$l_{\mathrm{QCD}} = \frac{\hbar}{m_p c}$
Mass (M)	$m_{\mathrm{QCD}} = m_p \$
Time (T)	$t_{\mathrm{QCD}} = \frac{\hbar}{m_p c^2}$
Electric charge (Q)	$q_{\mathrm{QCD}} = e \$
Temperature (Θ)	$T_{\mathrm{QCD}} = \frac{m_p c^2}{k}$

$c = 1 \$

$e = 1 \$

$m_p = 1 \$

$\hbar = 1 \$

$k = 1 \$

$\frac{1}{4 \pi \epsilon_0} = \alpha$

The electron mass is replaced with that of the proton and the permittivity of free space is not fixed by definition. Strong units are convenient for work in QCD and nuclear physics, where quantum mechanics and relativity are omnipresent and the proton is an object of central interest^[3]. In QCD, any observed variation over space or time in the value of α is attributed to variation in $\epsilon_0 \$ .

[edit] Geometrized units

Main article: Geometrized unit system

$c = 1 \$

$G = 1 \$

The geometrized unit system is not a completely defined or unique system. In this system, the base physical units are chosen so that the speed of light and the gravitational constant are set equal to unity leaving latitude to also set some other constant such as the Boltzmann constant and Coulomb force constant equal to unity:

$k = 1 \$

$\frac{1}{4 \pi \epsilon_0} = 1$

If the reduced Planck constant is also set equal to unity,

$\hbar = 1 \$

then geometrized units are identical to Planck units.

[edit] N-body units

Quantity	Expression
Length (R)	$\frac{1}{R} = \frac{1}{N(N-1)} \sum_{i=1}^{N} \sum_{j=1}^{N} \frac{1}{r_j-r_i}$
Mass (M)	$M = \sum_{i=1}^{N} m_i$

$M = 1 \$

$G = 1 \$

$R = 1 \$

N-body units are a completely self-contained system of units used for N-body simulations of self gravitating systems in astrophysics. In this system, the base physical units are chosen so that the total mass (M), the gravitational constant (G) and the virial radius (R) are set equal to unity. The underlying assumption is that the system of N objects (stars) satisfies the virial theorem. The consequence of standard N-body units is that the velocity dispersion of the system is $v = 1/\sqrt{2}$ and that the dynamical -crossing- time scales as $t = 2\sqrt{2}$ . The first mention of standard N-body units was by Michel Hénon (1971) [4]. They were taken up by Haldan Cohn (1979) [5] and later widely advertised and generalized by Douglas Heggie and Robert Mathieu (1986). [6]

[edit] See also

[edit] References

^ Kowalski, Ludwik, 1986, "A Short History of the SI Units in Electricity," The Physics Teacher 24(32): 97-99.
^ Ray, T.P. (1981). "Stoney's Fundamental Units". Irish Astronomical Journal 15: 152.
^ Wilczek, Frank, 2007, "Fundamental Constants," Frank Wilczek web site.

[edit] External links

The NIST website(National Institute of Standards and Technology) is a convenient source of data on the commonly recognized constants.
K.A. Tomilin: NATURAL SYSTEMS OF UNITS; To the Centenary Anniversary of the Planck System A comparative overview/tutorial of various systems of natural units having historical use.

[0] Kowalski, Ludwik, 1986, "A Short History of the SI Units in Electricity," The Physics Teacher 24(32): 97-99.

[1] Ray, T.P. (1981). "Stoney's Fundamental Units". Irish Astronomical Journal 15: 152.

[2] Wilczek, Frank, 2007, "Fundamental Constants," Frank Wilczek web site.

[1]

[2]

[3]

Natural units

From Wikipedia, the free encyclopedia

Contents

[edit] Introduction

[edit] Candidate physical constants used in natural unit systems

[edit] Planck units

[edit] Stoney units

[edit] "Schrödinger" units

[edit] Atomic units (Hartree)

[edit] Electronic system of units

[edit] Quantum chromodynamical system of units (Strong)

[edit] Geometrized units

[edit] N-body units

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages