Heat transfer

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Heat transfer is the transition of thermal energy or simply heat from a hotter object to a cooler object ("object" in this sense designating a complex collection of particles which is capable of storing energy in many different ways). When an object or fluid is at a different temperature than its surroundings or another object, transfer of thermal energy, also known as heat transfer, or heat exchange, occurs in such a way that the body and the surroundings reach thermal equilibrium. Heat transfer always occurs from a higher-temperature object to a cooler temperature one as described by the second law of thermodynamics. Where there is a temperature difference between objects in proximity, heat transfer between them can never be stopped; it can only be slowed.

Contents

[edit] Conduction

Main article: Heat conduction

Conduction is the transfer of heat by direct contact of particles of matter. The transfer of energy could be primarily by elastic impact as in fluids or by free electron diffusion as predominant in metals or phonon vibration as predominant in insulators. In other words, heat is transferred by conduction when adjacent atoms vibrate against one another, or as electrons move from atom to atom. Conduction is greater in solids, where atoms are in constant contact. In liquids (except liquid metals) and gases, the molecules are usually further apart, giving a lower chance of molecules colliding and passing on thermal energy.

Heat conduction is directly analogous to diffusion of particles into a fluid, in the situation where there are no fluid currents. This type of heat diffusion differs from mass diffusion in behaviour, only in as much as it can occur in solids, whereas mass diffusion is mostly limited to fluids.

Metals (eg. copper, platinum, gold, iron, etc.) are usually the best conductors of thermal energy. This is due to the way that metals are chemically bonded: metallic bonds (as opposed to covalent or ionic bonds) have free-moving electrons which are able to transfer of thermal energy rapidly through the metal.

As density decreases so does conduction. Therefore, fluids (and especially gases) are less conductive. This is due to the large distance between atoms in a gas: fewer collisions between atoms means less conduction. Conductivity of gases increases with temperature. Conductivity increases with increasing pressure from vacuum up to a critical point that the density of the gas is such that that molecules of the gas may be expected to collide with each other before they transfer heat from one surface to another. After this point in density, conductivity increases only slightly with increasing pressure and density.

To quantify the ease with which a particular medium conducts, engineers employ the thermal conductivity, also known as the conductivity constant or conduction coefficient, k. In thermal conductivity k is defined as "the quantity of heat, Q, transmitted in time (t) through a thickness (L), in a direction normal to a surface of area (A), due to a temperature difference (ΔT) [...]." Thermal conductivity is a material property that is primarily dependent on the medium's phase, temperature, density, and molecular bonding.

A heat pipe is a passive device that is constructed in such a way that it acts as though it has extremely high thermal conductivity.

Transient Conduction vs. steady state conduction. Steady state conduction is the form of conduction which happens when the temperature difference is constant, so that an equlibration time, the spatial distribution of temperatures in an object does not change (for example, a bar may be cold at one end and hot at the other, but the gradient of temperatures along the bar do not change with time). There also exist situations wherein the temperature drop or raise occurs more drastically, such as when a hot copper ball is dropped into oil at a low temperature, and the interest is in analysing the spatial change of temperature in the object over time. This mode of heat conduction can be referred to as unsteady mode of conduction or transient conduction. Analysis of these systems is more complex and (except for simple shapes) calls in for the application of approximation theories.

Lumped System Analysis. A common approximation in transient conduction, which may be used whenever heat conduction within an object is much faster than heat conduction across the boundary of the object, is Lumped system analysis. This is a method of approximation that suitably reduces one aspect of the transient conduction system (that within the object) to an equivalent steady state system (that is, it is assumed that the temperature within the object is completely uniform, although its value may be changing in time). In this method, a term known as the Biot number is calculated, which is defined as the ratio of resistance to heat transfer across the object's boundary with a uniform bath of different temperature, to the conductive heat resistance within the object. When the thermal resistance to heat transferred into the object is less than the resistance to heat being diffused completely within the object, the Biot number is small, and the approximation of spatially uniform temperature within the object can be used. As this is a mode of approximation, the Biot number must be less than 0.1 for accurate approximation and heat transfer analysis. The mathematical solution to the lumped system approximation gives Newton's law of cooling, discussed below.

Even if the Biot number is not less than 0.1, analysis can be continued, but the accuracy of the result reduces. This mode of analysis has been applied to forensic sciences to analyse the time of death of humans. Also it can be applied to HVAC (heating, ventilating and air-conditioning, or building climate control), to ensure more nearly instantaneous effects of a change in comfort level setting.[1]

[edit] Convection

Main articles: convection and convective heat transfer

Convection is the transfer of heat energy through a moving fluid at various temperatures. It is mainly a combination of diffusion and the bulk motion of molecules. When the mass of the fluid is in contact with a hot surface, its molecules expand and scatter, causing the mass of fluid to become less dense. When this happens, the fluid is displaced vertically or horizontally while the cooler fluid gets denser and sinks. Thus the hotter volume transfers heat towards the cooler volumes of that fluid. [2]

There are two types of Convective Heat Transfer: • Natural Convection: is when the fluid motion is caused by the density variations that result from the temperature distributions in heat transfer and gravitational forces. These variations in density can be described by buoyancy forces (body of force proportional to density gradient), thus buoyancy is the driving force for natural convection. The change in density of the boundary layer while heating will cause the fluid to rise and be replaced by a cooler fluid. - Example: Transfer of heat from hot water to a radiator in a room • Forced Convection: unlike natural convection, forced convection is not related to the use of heat transfer between fluids but rather an external source such as pumps and fans. It creates an artificially induced convection current. [3]

Internal and external flow can also classify convection. Internal flow occurs when the fluid is enclosed by a solid boundary such as a flow through a pipe. An external flow occurs when the fluid extends indefinitely without encountering a solid surface. Both these convections, either natural or forced, can be internal or external as they are independent of each other.[3]

The formula for convection is: [4]

q = hA(Ts − Tinfinity)

A is the surface area of heat transfer and Ts − Tinfinity is the difference between the final and the initial temperatures. The h is the heat transfer coefficient which depends on the physical properties of the fluid (such as temperature) and the physical situation in which convection occurs. Therefore, the heat transfer coefficient must be derived or found experimentally for every system analyzed. Formulae and correlations are available in many references to calculate heat transfer coefficients for typical configurations and fluids. For laminar flows the heat transfer coefficient is rather low compared to the turbulent flows. This is due to the turbulent flows having a thinner stagnant fluid film layer on the heat transfer surface. [5]

[edit] Heat transfer coefficients

This section may require cleanup to meet Wikipedia's quality standards.
This section may require copy-editing for grammar, style, cohesion, tone or spelling. You can assist by editing it now. A how-to guide is available. (March 2009)

The coefficients of heat transfers are important to realize the process of heat transfer characteristics. they include: 1. heat transfer coefficient h, which is expressed by:h=q/(Ts-T∞).h has units of W/m²•k, which is the reciprocal of Resistance. 2.Nusselt Number is expressed by Nu=hD/k. In this equation,h is the heat transfer coefficient(h,W/m²•k). D is the characteristic length(D,m). K is the thermal conductivity(k,W/m•k).This equation is aimed to build the Ratio of thermal convection to thermal conduction. 3.Prandtl Number(Pr) is expressed by Pr=cp•μ/k. the cp is the specific heat capacity,(cp,J/kg·k).K is the thermal conductivity(k,W/m•k).μ is the Dynamic viscosity (μ, kg/m·s). the Pr is to express the Ratio of the rates of thermal diffusion to the diffusion of momentum. 4.Reynolds Number is expressed by Re=ρuD/μ. ρ is the density of the fluid,(ρ,kg/m³).u is the fluid velocity,(u,m/s).μ is the Dynamic viscosity (μ, kg/m·s).D is the characteristic dimension-diameter for pipes,other values for different gometries(D,m).This equation presents the Ratio of the inertial force of the fluid to the viscous forces in the fluid,which is used as the criteria to indicate the boundaries between laminar,transitional and turbulent flow.The Reynolds Number could present the different flow with the criteria,such as: Re<2100-laminar, 2100<Re>4000-transitional,Re>4000-turbulent.Moreover, different geometries may have different transition number. 5. Grashof Number is presented by the equation:Gr=ρ2·L3·ΔT·β·g/μ2.ΔT is the difference of temperature,(k).β is the coefficient of volumetric expansion for the fluid,(k-1).g is the gravity acceleration,(g=9.18m/s). This equation is aimed to present the Ratio of the buoyancy forces to the viscous forces in the fluid,which is used for Natural convection.For thoes number, it can be summaried by: Forced convection Nu=fn(Re,Pr) and Natural convection-Nu=fn(Pr,Gr).It is worth to mention the Dittus and Boelter Correlation Nu=h·D/k=0.023Re0.8·Prn. In this equation, the n=0.4 is for heating and 0.3 for cooling. The Correlations are only valid within limited ranges. [6]

[edit] Radiation

Main article: Thermal radiation

Radiation is the transfer of heat energy through empty space. All objects with a temperature above absolute zero radiate energy at a rate equal to their emissivity multiplied by the rate at which energy would radiate from them if they were a black body. No medium is necessary for radiation to occur; radiation works even in and through a perfect vacuum. The energy from the Sun travels through the vacuum of space before warming the earth. Also, the only way that energy can leave earth is by being radiated to space.

Both reflectivity and emissivity of all bodies is wavelength dependent. The temperature determines the wavelength distribution of the electromagnetic radiation as limited in intensity by Planck’s law of black-body radiation. For any body the reflectivity depends on the wavelength distribution of incoming electromagnetic radiation and therefore the temperature of the source of the radiation. The emissivity depends on the wave length distribution and therefore the temperature of the body itself. For example, fresh snow, which is highly reflective to visible light, (reflectivity about 0.90) appears white due to reflecting sunlight with a peak energy wavelength of about 0.5 micrometres. Its emissivity, however, at a temperature of about -5C, peak energy wavelength of about 12 micrometres, is 0.99.

Gases absorb and emit energy in characteristic wavelength patterns that are different for each gas.

Visible light is simply another form of electromagnetic radiation with a shorter wavelength (and therefore a higher frequency) than infrared radiation. The difference between visible light and the radiation from objects at conventional temperatures is a factor of about 20 in frequency and wavelength; the two kinds of emission are simply different "colours" of electromagnetic radiation.

[edit] Clothing and building surfaces, and radiative transfer

Lighter colours and also whites and metallic substances absorb less illuminating light, and thus heat up less; but otherwise colour makes little difference as regards heat transfer between an object at everyday temperatures and its surroundings, since the dominant emitted wavelengths are nowhere near the visible spectrum, but rather in the far infrared. Emissivities at those wavelengths have little to do with visual emissivities (visible colours); in the far infrared, most objects have high emissivities. Thus, except in sunlight, the colour of clothing makes little difference as regards warmth; likewise, paint colour of houses makes little difference to warmth except when the painted part is sunlit. The main exception to this is shiny metal surfaces, which have low emissivities both in the visible wavelengths and in the far infrared. Such surfaces can be used to reduce heat transfer in both directions; an example of this is the multi-layer insulation used to insulate spacecraft. Low-emissivity windows in houses are a more complicated technology, since they must have low emissivity at thermal wavelengths while remaining transparent to visible light.

[edit] Newton's law of cooling

A related principle, Newton's law of cooling, states that the rate of heat loss of a body is proportional to the difference in temperatures between the body and its surroundings, or environment. The law is

\frac{d Q}{d t} = h \cdot A(T_{0} - T_{\text{env}})
Q = Thermal energy in Joules
h = Heat transfer coefficient
A = Surface area of the heat being transferred
T0 = Temperature of the object's surface
Tenv = Temperature of the environment

This form of heat loss principle is sometimes not very precise; an accurate formulation may require analysis of heat flow, based on the (transient) heat transfer equation in a nonhomogeneous, or else poorly conductive, medium. An analog for continuous gradients is Fourier's Law.

The following simplification (called lumped system thermal analysis and other similar terms) may be applied, so long as it is permitted by the Biot number, which relates surface conductance to interior thermal conductivity in a body. If this ratio permits, it shows that the body has relatively high internal conductivity, such that (to good approximation) the entire body is at same uniform temperature as it is cooled from the outside, by the environment. If this is the case, these conditions give the behavior of exponential decay with time, of temperature of a body.

In such cases, the entire body is treated as lumped capacitance heat reservoir, with total heat content which is proportional to simple total heat capacity C , and T, the temperature of the body, or Q = CT From the definition of heat capacity: C = dQ/dT. Differentiating this equation with regard to time gives the identity dQ/dt = C (dT/dt). This may be used to replace dQ/dt in the equation above. Then, if T(t) is the temperature of such a body at time t , and Tenv is the temperature of the environment around the body:

\frac{d T(t)}{d t} = - r (T - T_{\mathrm{env}})

where r = hA/C is a positive constant characteristic of the system, which must be in units of 1/time, and is therefore sometimes expressed in terms of an time constant t0 given by: r = 1/t0 = ΔT/[dT/dt] . Thus, in thermal systems, t0 = C/hA. (The total heat capacity C of a system may be further represented by its mass-specific heat capacity cp multiplied by its mass m, so that the time constant is also mcp/hA).

The solution of this differential equation, by standard methods of integration and substitution of boundary conditions, gives:

T(t) = T_{\mathrm{env}} + (T(0) - T_{\mathrm{env}}) \ e^{-r t}. \quad

Here, T(t) is the temperature at time t, and T(0) is the initial temperature at zero time, or t = 0.

If:

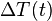\Delta T(t) \quad is defined as : T(t) - T_{\mathrm{env}} \ , \quad where \Delta T(0)\quad is the initial temperature difference at time 0,

then the Newtonian solution is written as:

\Delta T(t) = \Delta T(0) \ e^{-r t}. \quad

Uses: For example, simplified climate models may use Newtonian cooling instead of a full (and computationally expensive) radiation code to maintain atmospheric temperatures.

[edit] One dimensional Application, Using Thermal Circuits

A very useful concept used in heat transfer applications is the representation of thermal transfer by what is known as thermal circuits. A thermal circuit is the representation of the resistance to heat flow as though it were an electric resistor. The heat transferred is analogous to the current and the thermal resistance is analogous to the electric resistor. The value of the thermal resistance for the different modes of heat transfer are calculated as the denominators of the developed equations. The thermal resistances of the different modes of heat transfer are used in analyzing combined modes of heat transfer. The equations describing the three heat transfer modes and their thermal resistances, as discussed previously are summarized in the table below:

In cases where there is heat transfer through different media (for example through a composite), the equivalent resistance is the sum of the resistances of the components that make up the composite. Likely, in cases where there are different heat transfer modes, the total resistance is the sum of the resistances of the different modes. Using the thermal circuit concept, the amount of heat transferred through any medium is the quotient of the temperature change and the total thermal resistance of the medium. As an example, consider a composite wall of cross- sectional area A. The composite is made of an L1 long cement plaster with a thermal coefficient k1 and L2 long paper faced fiber glass, with thermal coefficient k2. The left surface of the wall is at Ti and exposed to air with a convective coefficient of hi. The Right surface of the wall is at To and exposed to air with convective coefficient ho.

Using the thermal resistance concept heat flow through the composite is as follows:

[edit] Insulation and radiant barriers

Main articles: Thermal insulation and Radiant barrier

Thermal insulators are materials specifically designed to reduce the flow of heat by limiting conduction, convection, or both. Radiant barriers are materials which reflect radiation and therefore reduce the flow of heat from radiation sources. Good insulators are not necessarily good radiant barriers, and vice versa. Metal, for instance, is an excellent reflector and poor insulator.

The effectiveness of an insulator is indicated by its R- (resistance) value. The R-value of a material is the inverse of the conduction coefficient (k) multiplied by the thickness (d) of the insulator. The units of resistance value are in SI units: (K·m²/W)

{R} = {r \over k}

{C} = {Q \over m \Delta T}

Rigid fiberglass, a common insulation material, has an R-value of 4 per inch, while poured concrete, a poor insulator, has an R-value of 0.08 per inch.[7]

The effectiveness of a radiant barrier is indicated by its reflectivity, which is the fraction of radiation reflected. A material with a high reflectivity (at a given wavelength) has a low emissivity (at that same wavelength), and vice versa (at any specific wavelength, reflectivity = 1 - emissivity). An ideal radiant barrier would have a reflectivity of 1 and would therefore reflect 100% of incoming radiation. Vacuum bottles (Dewars) are 'silvered' to approach this. In space vacuum, satellites use multi-layer insulation which consists of many layers of aluminized (shiny) mylar to greatly reduce radiation heat transfer and control satellite temperature.

[edit] Critical Insulation Thickness

This section may require cleanup to meet Wikipedia's quality standards.
This section may require copy-editing for grammar, style, cohesion, tone or spelling. You can assist by editing it now. A how-to guide is available. (March 2009)

To reduce the rate of heat transfer, one would add insulating materials i.e with low thermal conductivity(k). The smaller the k value, the larger the corresponding thermal resistance(R)value.
The units of thermal conductivity(k) are W.m-1.K-1 (Watts per meter per Kelvin), therefore increasing width of insulation(x meters)decreases the k term and as discussed increases resistance.
This follows logic as increased resistance would be created with increased conduction path(x).
However, adding this layer of insulation also has the potential of increasing the surface area and hence thermal convection area(A).
An obvious example is a cylindrical pipe:
As insulation gets thicker, outer radius increases and therefore surface area increases.
The point where the added resistance of increasing insulation width becomes overshadowed by the effects of surface are is called the Critical Insulation Thickness. In simple cylindrical pipes:
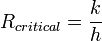{R_{critical}} = {k \over h} [8]


For a graph of this phenomenon in a cylidrical pipe example see: External Link: Critical Insulation Thickness diagram as at 26/03/09

[edit] Heat exchangers

Main article: Heat exchanger

A heat exchanger is a device built for efficient heat transfer from one fluid to another, whether the fluids are separated by a solid wall so that they never mix, or the fluids are directly contacted. Heat exchangers are widely used in refrigeration, air conditioning, space heating, power generation, and chemical processing. One common example of a heat exchanger is the radiator in a car, in which the hot radiator fluid is cooled by the flow of air over the radiator surface.

Common types of heat exchanger flows include parallel flow, counter flow, and cross flow. In parallel flow, both fluids move in the same direction while transferring heat; in counter flow, the fluids move in opposite directions and in cross flow the fluids move at right angles to each other. The common constructions for heat exchanger include shell and tube, double pipe, extruded finned pipe, spiral fin pipe, u-tube, and stacked plate. More information on heat exchanger flows and arrangements can be found in the heat exchanger article.

When engineers calculate the theoretical heat transfer in a heat exchanger, they must contend with the fact that the driving temperature difference between the two fluids varies with position. To account for this in simple systems, the log mean temperature difference (LMTD) is often used as an 'average' temperature. In more complex systems, direct knowledge of the LMTD is not available and the number of transfer units (NTU) method can be used instead.

[edit] Boiling heat transfer

See also: boiling and critical heat flux

Heat transfer in boiling fluids is complex but of considerable technical importance. It is characterised by an s-shaped curve relating heat flux to surface temperature difference (see say Kay & Nedderman 'Fluid Mechanics & Transfer Processes', CUP, 1985, p529).

At low driving temperatures, no boiling occurs and the heat transfer rate is controlled by the usual single-phase mechanisms. As the surface temperature is increased, local boiling occurs and vapour bubbles nucleate, grow into the surrounding cooler fluid, and collapse. This is sub-cooled nucleate boiling and is a very efficient heat transfer mechanism. At high bubble generation rates the bubbles begin to interfere and the heat flux no longer increases rapidly with surface temperature (this is the departure from nucleate boiling DNB). At higher temperatures still, a maximum in the heat flux is reached (the critical heat flux). The regime of falling heat transfer which follows is not easy to study but is believed to be characterised by alternate periods of nucleate and film boiling. Nukleate boiling slowing the heat transfer due to gas phase {bubbles} creation on the heater surface, as mentioned, gas phase thermal conductivity is much lower than liquid phase thermal conductivity, so the outcome is a kind of "gas thermal barrier".

At higher temperatures still, the hydrodynamically quieter regime of film boiling is reached. Heat fluxes across the stable vapour layers are low, but rise slowly with temperature. Any contact between fluid and the surface which may be seen probably leads to the extremely rapid nucleation of a fresh vapour layer ('spontaneous nucleation').

[edit] Condensation heat transfer

Condensation occurs when a vapor is cooled and changes its phase to a liquid. Condensation heat transfer, like boiling, is of great significance in industry. During condensation, the latent heat of vaporization must be released. The amount of the heat is the same as that absorbed during vaporization at the same fluid pressure.

There are several modes of condensation:

  • Homogeneous condensation (as during a formation of fog).
  • Condensation in direct contact with subcooled liquid.
  • Condensation on direct contact with a cooling wall of a heat exchanger-this is the most common mode used in industry:
    • Filmwise condensation (when a liquid film is formed on the subcooled surface, usually occurs when the liquid wets the surface).
    • Dropwise condensation (when liquid drops are formed on the subcooled surface, usually occurs when the liquid does not wet the surface). Dropwise condensation is difficult to sustain reliably; therefore, industrial equipment is normally designed to operate in filmwise condensation mode.

[edit] Heat transfer in education

Heat transfer is typically studied as part of a general chemical engineering or mechanical engineering curriculum. Typically, thermodynamics is a prerequisite to undertaking a course in heat transfer, as the laws of thermodynamics are essential in understanding the mechanism of heat transfer. Other courses related to heat transfer include energy conversion, thermofluids and mass transfer.

Heat transfer methodologies are used in the following disciplines, among others:

[edit] See also

[edit] Other fundamental engineering topics

[edit] References

  1. ^ Heat Transfer - A Practical Approach by Yugnus A Cengel
  2. ^ http://biocab.org/Heat_Transfer.html Biology Cabinet organization, April 2006, “Heat Transfer”, Accessed 20/03/09
  3. ^ http://www.engineersedge.com/heat_transfer/convection.htm Engineers Edge, 2009, “Convection Heat Transfer”,Accessed 20/03/09
  4. ^ Louis C. Burmeister, (1993) “Convective Heat Transfer”, 2nd ed. Publisher Wiley-Interscience, p 107 ISBN 047157709X, 9780471577096, Google Book Search. Accessed 20-03-09
  5. ^ http://www.engineersedge.com/heat_transfer/convection.htm Engineers Edge, 2009, “Convection Heat Transfer”,Accessed 20/03/09
  6. ^ John Kavangh,Heat Transfer Convection slide, Department of Chemical Engineering, The University of Sydney
  7. ^ Two websites: E-star and Coloradoenergy
  8. ^ http://mechatronics.atilim.edu.tr/courses/mece310/ch9mechatronics.ppt. Dr. Şaziye Balku: Notes including Critical Insulation Thickness as at 26/03/09
  • Class notes of Dr. Rong-Yaw Chen, Department of Mechanical Engineering, NJIT[1]

[edit] Related journals

  • Heat Transfer Engineering[2]
  • Experimental Heat Transfer[3]
  • International Journal of Heat and Mass Transfer[4]
  • ASME Journal of Heat Transfer[5]
  • Numerical Heat Transfer Part A[6]
  • Numerical Heat Transfer Part B[7]
  • Nanoscale and Microscale Thermophysical Engineering[8]
  • Journal of Enhanced Heat Transfer[9]

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Heat_transfer"
Personal tools