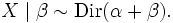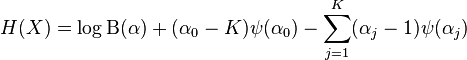Dirichlet distribution
From Wikipedia, the free encyclopedia
In probability and statistics, the Dirichlet distribution (after Johann Peter Gustav Lejeune Dirichlet), often denoted Dir(α), is a family of continuous multivariate probability distributions parametrized by the vector α of positive reals. It is the multivariate generalization of the beta distribution, and conjugate prior of the categorical distribution and multinomial distribution in Bayesian statistics. That is, its probability density function returns the belief that the probabilities of K rival events are xi given that each event has been observed αi − 1 times.
Contents |
[edit] Probability density function
The Dirichlet distribution of order K ≥ 2 with parameters α1, ..., αK > 0 has a probability density function with respect to Lebesgue measure on the Euclidean space RK–1 given by
for all x1, ..., xK–1 > 0 satisfying x1 + ... + xK–1 < 1, where xK is an abbreviation for 1 – x1 – ... – xK–1. The density is zero outside this open (K − 1)-dimensional simplex.
The normalizing constant is the multinomial beta function, which can be expressed in terms of the gamma function:
[edit] Properties
Let  , meaning that the first K – 1 components have the above density and
, meaning that the first K – 1 components have the above density and
Define 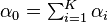 . Then
. Then
in fact, the marginals are Beta distributions:
Furthermore,
The mode of the distribution is the vector (x1, ..., xK) with
The Dirichlet distribution is conjugate to the multinomial distribution in the following sense: if
where βi is the number of occurrences of i in a sample of n points from the discrete distribution on {1, ..., K} defined by X, then
This relationship is used in Bayesian statistics to estimate the hidden parameters, X, of a discrete probability distribution given a collection of n samples. Intuitively, if the prior is represented as Dir(α), then Dir(α + β) is the posterior following a sequence of observations with histogram β.
[edit] Entropy
If X is a Dir(α) random variable, then we can use the exponential family differential identities to get an analytic expression for the expectation of logXi:
- E[logXi] = ψ(αi) − ψ(α0)
where ψ is the digamma function. This yields the following formula for the information entropy of X:
[edit] Aggregation
If  , then
, then  . This aggregation property may be used to derive the marginal distribution of Xi mentioned above.
. This aggregation property may be used to derive the marginal distribution of Xi mentioned above.
[edit] Neutrality
(main article: neutral vector).
If  , then the vector~X is said to be neutral[1] in the sense that X1 is independent of
, then the vector~X is said to be neutral[1] in the sense that X1 is independent of  and similarly for
and similarly for  .
.
Observe that any permutation of X is also neutral (a property not possessed by samples drawn from a generalized Dirichlet distribution).
[edit] Related distributions
- If, for

-
- then
- and
- Though the Xis are not independent from one another, they can be seen to be generated from a set of K independent gamma random variables. Unfortunately, since the sum V is lost in forming X, it is not possible to recover the original gamma random variables from these values alone. Nevertheless, because independent random variables are simpler to work with, this reparametrization can still be useful for proofs about properties of the Dirichlet distribution.
- The following is a derivation of Dirichlet distribution from Gamma distribution.
- Let Yi, i=1,2,...K be a list of i.i.d variables, following Gamma distributions with the same scale parameter θ
-
- then the joint distribution of Yi, i=1,2,...K is
- Through the change of variables, set
- Then, it's easy to derive that
- Then, the Jacobian is
- It means
- So,
- By integrating out γ, we can get the Dirichlet distribution as the following.
-
- According to the Gamma distribution,

- Finally, we get the following Dirichlet distribution
- where XK is (1-X1 - X2... -XK-1)
- Multinomial opinions in subjective logic are equivalent to Dirichlet distributions.
[edit] Random number generation
[edit] Gamma distribution
A fast method to sample a random vector  from the K-dimensional Dirichlet distribution with parameters
from the K-dimensional Dirichlet distribution with parameters  follows immediately from this connection. First, draw K independent random samples
follows immediately from this connection. First, draw K independent random samples  from gamma distributions each with density
from gamma distributions each with density
and then set
[edit] Marginal beta distributions
A less efficient algorithm[2] relies on the univariate marginal and conditional distributions being beta and proceeds as follows. Simulate x1 from a  distribution. Then simulate
distribution. Then simulate  in order, as follows. For
in order, as follows. For  , simulate φj from a
, simulate φj from a  distribution, and let
distribution, and let  . Finally, set
. Finally, set  .
.
[edit] Intuitive interpretations of the parameters
[edit] String cutting
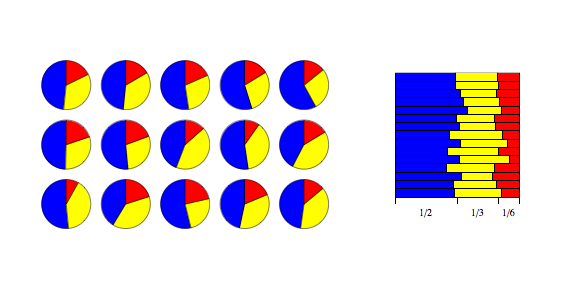
One example use of the Dirichlet distribution is if one wanted to cut strings (each of initial length 1.0) into K pieces with different lengths, where each piece had, on average, a designated average length, but allowing some variation in the relative sizes of the pieces. The α/α0 values specify the mean lengths of the cut pieces of string resulting from the distribution. The variance around this mean varies inversely with α0.
[edit] Pólya urn
Consider an urn containing balls of K different colors. Initially, the urn contains α1 balls of color 1, α2 balls of color 2, and so on. Now perform N draws from the urn, where after each draw, the ball is placed back into the urn with another ball of the same color. In the limit as N approaches infinity, the proportions of different colored balls in the urn will be distributed as  .[3]
.[3]
Note that each draw from the urn modifies the probability of drawing a ball of any one color from the urn in the future. This modification diminishes with the number of draws, since the relative effect of adding a new ball to the urn diminishes as the urn accumulates increasing numbers of balls. This "diminishing returns" effect can also help explain how large α values yield Dirichlet distributions with most of the probability mass concentrated around a single point on the simplex.
[edit] See also
- beta distribution
- binomial distribution
- categorical distribution
- generalized Dirichlet distribution
- latent Dirichlet allocation
- multinomial distribution
- multivariate Polya distribution
[edit] References
- ^ Connor, Robert J. (1969). "Concepts of Independence for Proportions with a Generalization of the Dirichlet Distribution". journal of the American statistical association 64 (325): 194-206. doi:.
- ^ A. Gelman and J. B. Carlin and H. S. Stern and D. B. Rubin (2003). Bayesian Data Analysis (2nd ed.). pp. 582. ISBN 1-58488-388-X.
- ^ Blackwell, David (1973). "Ferguson Distributions Via Polya Urn Schemes". Ann Stat 1 (2): 353-355. doi:.
[edit] External links
- Dirichlet Distribution
- Estimating the parameters of the Dirichlet distribution
- Non-Uniform Random Variate Generation, Luc Devroye



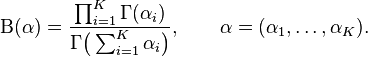
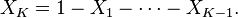
![\mathrm{E}[X_i] = \frac{\alpha_i}{\alpha_0},](http://upload.wikimedia.org/math/7/6/9/76941af82bb219bd4ecf15bd866df3e7.png)
![\mathrm{Var}[X_i] = \frac{\alpha_i (\alpha_0-\alpha_i)}{\alpha_0^2 (\alpha_0+1)},](http://upload.wikimedia.org/math/1/1/f/11f1756341eabbbac8585d2c0f0341b9.png)

![\mathrm{Cov}[X_iX_j] = \frac{- \alpha_i \alpha_j}{\alpha_0^2 (\alpha_0+1)}.](http://upload.wikimedia.org/math/d/3/a/d3ac1b8466594e22e4c3203fd86c017e.png)