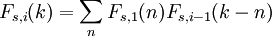Dice
From Wikipedia, the free encyclopedia
- For other uses, see either Die or Dice (disambiguation).
A die (plural dice, from Old French dé, from Latin datum "something given or played"[1]) is a small polyhedral object, usually cubic, used for generating random numbers or other symbols. This makes dice suitable as gambling devices, especially for craps or sic bo, or for use in non-gambling tabletop games.
A traditional die is a cube (often with corners slightly rounded), marked on each of its six faces with a different number of circular patches or pits called pips. All of these pips have the same appearance within a pair, or larger set of dice, and are sized for ease of recognizing the pattern formed by the pips on a face. The design as a whole is aimed at each die providing one randomly determined integer, in the range from one to six, with each of those values being equally likely.
More generally, a variety of analogous devices are often described as dice, but necessarily in a context, or with a word or two preceding "die" or "dice", that avoids the assumption that traditional dice are intended. Such specialized dice may have cubical or other polyhedral shapes, with faces marked with various collections of symbols, and be used to produce other random results than one through six. There are also "loaded" or "crooked" dice (especially otherwise traditional ones), meant to produce skewed or even predictable results, for purposes of deception or amusement.
Contents |
[edit] Ordinary dice
Common dice are small cubes 1 to 3 cm along an edge (16 mm being the standard), whose faces are numbered from one to six (usually by patterns of dots called pips). It is traditional to combine pairs of numbers that total seven to opposite faces (it has been since at least classical antiquity); this implies that at one vertex the faces 1, 2 and 3 intersect. It leaves one other abstract design choice: the faces representing 1, 2 and 3 respectively can be placed in either clockwise or counterclockwise order about this vertex.
The pips on traditional European dice are arranged in specific circular patterns. The face with two usually has the dots in opposite corners, with the third face containing one between these two. The fourth face has one in each corner, and the fifth adds one in the center, forming a quincunx. The final face has two rows of three pips along opposite edges of the face. Pips on Asian-style dice are in a similar pattern, but are typically closer to the centre of the die, and the "one" pip is larger than the others. A unique feature of Asian dice is the fact that the pips for both "one" and "four" are colored red. Why this is so is unknown. But it is suggested that an entirely black and white color combination on the one side would be unlucky and red (a lucky color in Chinese culture) would counteract this. Several legends also mention that the "four" side is colored red because a Chinese emperor (one legend said it was a Ming dynasty emperor, while another stated it was Chung Tsung) ordered it as "fours" helped him win a dice game (sugoroku) against his empress. This story, however, is questionable at best, as it is also probable that "red fours" are also of common Indian origin.[2][3]. Another reason why the "four" side might be colored red is because in Asian cultures, the number four is seen as unlucky, like the number thirteen in Western culture, and as mentioned before, it is colored red so that the luckiness of the red counteracts the unluckiness of the four.
Dice are thrown to provide random numbers for gambling and other games, and thus are a type of hardware random number generator. The result of a die roll is random in the sense of lacking predictability, not lacking cause. Exactly how dice are thrown determines how they will land according to the laws of classical mechanics. However, dice also can exhibit sensitive dependence on initial conditions, making it difficult to predict the outcome of a die roll even with good information about exactly how it is thrown. Also, because the numbers on typical dice are marked with small indentations, slightly more material is removed from the higher numbered faces. This results in a small bias, and they do not provide fair (uniform) random numbers. The bias is reduced somewhat in the Japanese die with its oversized single pip (pictured). Casino dice have markings that are flush with the surface and come very close to providing true uniformly distributed random numbers.
Dice are thrown, singly or in groups, from the hand or from a cup or box designed for the purpose, onto a flat surface. The face of each die that is uppermost when it comes to rest provides the value of the throw. A typical dice game today is craps, wherein two dice are thrown at a time, and wagers are made on the total value of up-facing pips on the two dice. They are also frequently used to randomize allowable moves in board games, usually by deciding the distance through which a piece will move along the board; examples of this are ludo and backgammon.
[edit] Precision dice
Precision casino dice, used for the game of craps, may have a polished finish, making them transparent, or a sand finish, making them translucent. Casino dice have their pips drilled, and then filled flush with a paint of the same density as the acetate used for the dice, such that the dice remain in balance. In casino play, a stick of 5 dice are used, all stamped with a matching serial number to prevent a cheat from substituting a die.
Precision backgammon dice are also made with the pips filled in as with casino dice. While casino dice are noticeably larger than common dice, with sharp edges and corners, precision backgammon dice tend to be somewhat smaller. Their corners and edges are rounded to allow greater movement inside the dice cup and prevent chaotic rolls from damaging the playing surface.
[edit] Computer generated dice
Some computer games, such as clones of board games, must use computer generated dice. The values are usually determined by a random number generator, then displayed as a visual representation of a dice. Some sites which show examples of computer generated random dice are GoTinker [4] and RANDOM.ORG [5]
[edit] History

The invention of dicing is attributed to India by some accounts.[6][7] Some of the earliest archaeological evidence of oblong gambling dice have been found in Harrapan sites such as Kalibangan, Lothal, Ropar and surrounding areas dating back to the third millennium BCE, which were used for gambling.[8][9]
The oblong or cubical dice (akṣa) is the precursor of the more primitive vibhīṣaka—small, hard nuts drawn randomly to obtain factors of a certain integer.[10] Early references to the dicing can be found in the Ṛg Veda (c. early 2nd millennium BCE)[11][8] as well as the newer Atharva Veda (c. late 2nd millennium ~ early 1st millennium BCE).[12][8] It is also mentioned in the great Hindu epic, the Mahabharata, where Yudhisthira plays a game of dice against the Kauravas for the northern kingdom of Hastinapura.
The use of dice is believed to have later spread to Persia from India, influencing Persian board games.[13] Excavations at the Shahr-i Sokhta (Persian شهر سوخته , literally "The Burnt City'") archaeological site in south-eastern Iran yielded one of the oldest known dice which were excavated as part of a 5000-year-old backgammon set, which was probably imported from India.[14][15]
Dice were probably originally made from the ankle bones (specifically the talus or "astragalus") of hoofed animals (such as oxen), colloquially known as "knucklebones", which are approximately tetrahedral. Modern Mongolians still use such bones, known as shagai, for games and fortunetelling. In addition to bone, ivory, wood, metal, and stone materials have been commonly used. Recently, the use of plastics, including cellulose acetate and Bakelite, is nearly universal. It is almost impossible to trace clearly the development of dice as distinguished from knucklebones, because ancient writers confused the two. It is certain, however, that both were used in prehistoric times.
There are several biblical references to "casting lots", as in Psalm 22, indicating that it had become commonplace in the region as of the time of King David. In its primitive form knucklebones was essentially a game of skill played by women and children. In a derivative form of knucklebones, the four sides of the bones received different values and were counted as with modern dice. Gambling with three or sometimes two dice was a very popular form of amusement in Greece, especially with the upper classes, and was an almost invariable accompaniment to symposia.
The Romans were passionate gamblers, especially in the luxurious days of the Roman Empire, and dicing was a favorite form, though it was forbidden except during the Saturnalia. Horace derided what he presented as a typical youth of the period, who wasted his time amid the dangers of dicing instead of taming his charger and giving himself up to the hardships of the chase. Throwing dice for money was the cause of many special laws in Rome. One of these stated that no suit could be brought by a person who allowed gambling in his house, even if he had been cheated or assaulted. Professional gamblers were common, and some of their loaded dice are preserved in museums. The common public-houses were the resorts of gamblers, and a fresco is extant showing two quarrelling dicers being ejected by the indignant host. 20 sided dice date back to Roman times, as far back as 2nd century AD [1].
Tacitus states that the Germans were passionately fond of dicing, so much so, indeed, that, having lost everything, they would even stake their personal liberty. Centuries later, during the Middle Ages, dicing became the favorite pastime of the knights, and both dicing schools and guilds of dicers existed. After the downfall of feudalism the famous German mercenaries called landsknechts established a reputation as the most notorious dicing gamblers of their time. Many of the dice of the period were curiously carved in the images of men and beasts. In France both knights and ladies were given to dicing. This persisted through repeated legislation, including interdictions on the part of St. Louis in 1254 and 1256.
In China, India, Japan, Korea, and other Asiatic countries, dice have always been popular and are so still. The markings on Chinese dominoes evolved from the markings on dice, taken two at a time.
[edit] Terms
While the terms ace, deuce, trey, cater, cinque and sice are hardly common today having been replaced with the ordinary names of the numbers one to six, they are still used by some professional gamblers to describe the different sides of the dice. Ace is from the Latin as, meaning "a unit"[16]; the others are the numbers 2–6 in old French. (The dice game marketed as Kismet uses ace, deuce, and trey.)
[edit] Notation
In many modern gaming contexts, the count and number of sides of dice to be rolled at any given time is reduced to a common set of notations. Typically this involves the lower-case letter "d", preceded by a die count and followed by (optionally) the number of sides of the dice. For example, 6d8 or 2d6; the former meaning "six eight-sided dice," and the latter meaning "two six-sided dice." Addition or various other arithmetic operations are often added at the end as well, e.g. 3d6+4 "three six-sided dice plus four to the outcome thereof".
[edit] Crooked dice
"Crooked dice" refers to dice that have been altered in some way to change the distribution of their outcome.
[edit] Loaded dice
A loaded or gaffed or cogged die is a die that has been tampered with to land with a selected side facing upwards more often than it otherwise would simply by chance. There are methods of creating loaded dice, including having some edges round and other sharp and slightly off square faces. If the dice are not transparent, weights can be added to one side or the other. They can be modified to produce winners ("passers") or losers ("miss-outs"). "Tappers" have a drop of mercury in a reservoir at the center of the cube, with a capillary tube leading to another mercury reservoir at the side of the cube. The load is activated by tapping the die on the table so that the mercury leaves the center and travels to the side. Often one can see the circle of the cut used to remove the face and bury the weight. In a professional die, the weight is inserted in manufacture; in the case of a wooden die, this can be done by carving the die around a heavy inclusion, like a pebble around which a tree has grown.
A variable loaded die is hollow with a small weight and a semi-solid substance inside, usually wax, whose melting point is just lower than the temperature of the human body. This allows the cheater to change the loading of the die by breathing on it or holding it firmly in hand, causing the wax to melt and the weight to drift down, making the chosen opposite face more likely to land up. A less common type of variable die can be made by inserting a magnet into the die and embedding a coil of wire in the game table. Then, either leave the current off and let the die roll unchanged or run current through the coil to increase the likelihood that the north side or the south side will land on the bottom depending on the direction of the current.
Plastic dice can be biased to roll a certain number by heating them (for example in an oven) with the desired face upward, so that the plastic will soften slightly and "pool" at the opposite (bottom) side of the die without showing much, if any, visible distortion.
Transparent acetate dice, used in all reputable casinos, are harder to tamper with.
[edit] Cheat dice
Cheat dice (see below) are often sold as loaded dice but usually are not technically loaded.
[edit] Shaved dice
A die can be "shaved" on one side i.e. slightly shorter in one dimension, making it slightly rectangular and thus affecting its outcome. One countermeasure employed by casinos against shaved dice is to measure the dice with a micrometer.
[edit] Iced Dice
Iced dice have lead in them, making them land on the 6 side more. The "ice" refers to the lead in the dice.
[edit] Variants
[edit] Dice with faces other than digit sequences
As noted, the faces of most dice are labeled using an unbroken series of whole numbers, starting at one (rarely zero), expressed with either pips or digits. Common exceptions include:
- color dice (e.g., with the colors of the playing pieces used in a game)
- Poker dice, with labels reminiscent of playing cards. Several varieties exist, but the most common contain the following pattern: 9♣, 10♦, Jack (blue), Queen (green), King (red), A♠
- dice with letters (e.g. in Boggle)
- average dice (2, 3, 3, 4, 4, 5) (In some war games, units are identified as regulars or irregulars. Because regulars are more predictable, the strength of a regular unit is multiplied by an average die. For this reason, average dice are jocularly called regular dice.)
- cheat dice, such as:
- one face each with two through five, and two with sixes, or
- for craps, a pair of dice in which one die has five on each face, and its mate has a mixture of twos and sixes, guaranteeing rolls of seven or 11.
- dice with a single sequence of markings repeated multiple times, for example:
- a cubical die numbered twice from 1 to 3, or thrice from 1 to 2.
- cubical dice numbered twice from 0 to 2. Dice rolls with these dice have the same expected value as the number of dice thrown.
- icosahedral dice numbered twice from 1 to 10 (commonly used in Dungeons & Dragons before the popularization of ten-sided dice).
- Fudge dice, numbered twice from −1 to 1, represented as −, blank, +.
- random direction dice, also known as scatter dice. The dice have arrows on each side; the outcome of a roll is a random direction. Scatter dice are used in tabletop wargames such as Warhammer Fantasy Battle to determine random movements of troops, wind direction or direction of misfired arms. Note that this is an unusual case where the majority of the time the die is read not according to which symbol is shown on its uppermost face, but its compass orientation.
- A doubling cube with the numbers 2, 4, 8, 16, 32, and 64 is used in backgammon and some other boardgames. This die is not actually rolled; it is used to denote the current stakes of the game. There is also a doubling octahedron with 1, 2, 4, 8, 16, 32, 64, and 128.
- Some board games use dice with positive and negative numbers for use in gain or loss of something.
- Sicherman dice, a pair having the same odds of rolling a given sum as a pair of standard six-sided dice, but with different markings: one die has 1, 3, 4, 5, 6, and 8, and the other has 1, 2, 2, 3, 3, and 4. Sicherman dice are the only such alternative arrangement if positive whole numbers are used.
- I Ching dice such as
- Eight-sided dice bearing the eight trigrams
- Six-sided dice bearing yin and yang twice each, and old yin and old yang once each
- "Projector dice" which are clear and marked only on one of each pair of opposing faces. For a "six"-sided die, e.g., a clear twelve sided-shape is used. Rolled on an overhead projector such a die will have the top or bottom marking equally readable.
[edit] Non-cubical dice
Some dice are polyhedral other than cubical in shape. They became popular around the early 1950s among players of wargames and have since been used extensively in trading card games, German-style board games, and role-playing games. Although polyhedral dice are a relative novelty during modern times, some ancient cultures appear to have used them in games (as evidenced by the discovery of two icosahedral dice dating from the days of ancient Rome, currently on display in the British Museum). In modern times, such dice are typically plastic, and have faces bearing numerals rather than patterns of dots. Reciprocally symmetric numerals are distinguished with a dot in the lower right corner (6. vs 9.) or by being underlined (6 vs 9).
The platonic solids are commonly used to make dice of 4, 6, 8, 12, and 20 faces. Other shapes can be found to make dice with other numbers of faces, but other than the 10 sided, they are rarely used. (See Zocchihedron.) The 4-sided platonic solid is difficult to roll, and a few games like Daldøs use a 4 sided rolling pin instead.
A large number of different probability distributions can be obtained using these dice in various ways. For example, 10-sided dice (or 20-sided dice labeled with single digits) are often used in pairs to produce a uniform distribution of random percentages; they avoid number base conversions and are more convenient. Summing multiple dice produces a normal distribution (a "bell curve"), while eliminating high or low throws can be used to skew the distribution in various ways.
Using these techniques, games can closely approximate the real probability distributions of the events they simulate.
There is some controversy over whether manufacturing processes create genuinely "fair" or "honest" dice (dice that roll with even distributions over their number span). Casino dice are legally required to be fair; those used by others are subject to no legally required standards.
Spherical dice also exist; these function like the plain cubic dice, but have an octahedral internal cavity in which a weight moves which causes them to settle in one of six orientations when rolled. However, these dice are somewhat awkward in use because they require a flat and level surface to roll properly — an uneven surface often causes them to stop partway between two numbers, while a sloped surface will obviously cause the dice to keep rolling.
Cowry shells, Yut sticks or coins may be used as a kind of two-sided dice. Because of their lack of symmetry, cowry shells and Yut sticks are not likely to yield a uniform distribution, and the angle and speed of the throw may possibly affect the result.
[edit] Standard variations
The most common non-cubical dice — often sold in sets of five or six that are each differently shaped but with the same pair of background and marking colors — include one each of the five Platonic solids, which are symmetrical. The six-die versions add the pentagonal trapezohedron, in which the faces (identical to one another as to angles and edge lengths) each have two different lengths of side, and three different sizes of angle; the corners at which multiple faces meet are also of two different kinds.
| Sides | Shape | Notes | |
|---|---|---|---|
| 4 | tetrahedron | Each face has three numbers: they are arranged such that the upright number (which counts) is the same on all three visible faces. Alternatively, all of the sides have the same number in the lowest edge and no number on the top. This die does not roll well and thus it is usually thrown into the air instead. | |
| 6 | cube | A common die. The sum of the numbers on opposite faces is seven. | |
| 8 | octahedron | Each face is triangular; looks like two square pyramids attached base-to-base. Usually, the sum of the opposite faces is 9. | |
| 10 | pentagonal trapezohedron | Each face is kite-shaped; five of them meet at the same sharp corner (as at the top of the diagram in this row), and five at another equally sharp one; about halfway between them, a different group of three faces converges at each of ten blunter corners. The ten faces usually bear numbers from zero to nine, rather than one to ten (zero being read as "ten" in many applications), and often all odd numbered faces converge at one sharp corner, and the even ones at the other. | |
| 12 | dodecahedron | Each face is a regular pentagon. | |
| 20 | icosahedron | Faces are equilateral triangles. Typically, opposite faces add to twenty-one. A 2nd century AD Roman icosahedron die is in the collection of the British Museum, though the game it was used for is not known.[17] | |
[edit] Rarer variations
| Sides | Shape | Notes |
|---|---|---|
| 1 | sphere | Most commonly a joke die, this is just a sphere with a 1 marked on it. There exist spherical dice which include a spherical weight in a faceted internal cavity; the weight can rest in one of the corners of the cavity. The weight effectively pins one side of the sphere down, revealing the number directly opposite. |
| 2 | cylinder | This is nothing more than a coin shape with 1 marked on one side and 2 on the other. While some tasks in roleplaying require flipping a coin, it is usually referred to as such, and not as rolling a two-sided die. It is possible, however, to find dice of this sort for purchase, but they are rare, and can typically be found among other joke dice. |
| 3 | Rounded-off triangular prism | This is a rounded-off triangular prism, intended to be rolled like a rolling-pin style die. The die is rounded-off at the edges to make it impossible for it to somehow land on the triangular sides, which makes it look a bit like a jewel. When the die is rolled, one edge (rather than a side) appears facing upwards. On either side of each edge the same number is printed (from 1 to 3). The numbers on either side of the up-facing edge are read as the result of the die roll. Another possible shape is the "American Football" or "Rugby ball" shape, where the ends are pointed (with rounded points) rather than just rounded. |
| 5 | Triangular prism | This is a prism that is thin enough to land either on its "edge" or "face". When landing on an edge, the result is displayed by digits (2–4) close to the prism's top edge. The triangular faces are labeled with the digits 1 and 5. |
| 7 | Pentagonal prism | Similar in constitution to the 5-sided die. When landing on an edge, the topmost edge has pips for 1–5. The pentagonal faces are labeled with the digits 6 and 7. This kind of die is particularly odd since it has pips for five of its results and digits for two of them. Seven sided dice are used in a seven-player variant of backgammon. Some variants have heptagonal ends and rectangular faces. |
| 12 | rhombic dodecahedron | Each face is in the shape of a rhombus. |
| 14 | heptagonal trapezohedron | Each face is in the shape of a kite. |
| 16 | octagonal dipyramid | Each face is in the shape of an isosceles triangle. |
| 24 | tetrakis hexahedron | Each face is in the shape of an isosceles triangle. |
| 24 | deltoidal icositetrahedron | Each face is in the shape of a kite. |
| 30 | rhombic triacontahedron | Each face is in the shape of a rhombus (diamond-shaped). A thirty sided die is the largest multi-faced die that is a symmetrical polyhedron. It is considered to have the highest rate of generating random numbers due to its large array of numbers and natural spherical shape. Although it is not included in most dice kits, 30 sided die can be found in most hobby and game stores. |
| 34 | heptadecagonal trapezohedron | Each face is in the shape of a kite. |
| 50 | icosakaipentagonal trapezohedron | Similar to the 14- and 16-sided dice, the faces of the 50-sided die are kites, although very narrow. |
| 100 | Zocchihedron | 100-sided dice can be found in hobby and game stores, and such a die is used in some narrative role-playing games such as Dungeons & Dragons. They are not, however, a true polyhedron. A 100-sided die is made by taking a sphere and placing 100 equally spaced flat planes on the surface. The name Zocchihedron was taken from its creator, Lou Zocchi. A 100-sided die is equivalent one or two ten-sided dice, and so, even in role-playing games, the Zocchihedron is rarely seen. |
The full geometric set of "uniform fair dice" (face-transitive) are:
- Platonic solids: 5 regular polyhedra: (4, 6, 8, 12, 20 sides)
- Catalan solids: 13 Archimedean duals: (12, 24, 30, 48, 60, 120 sides)
- Bipyramids: infinite set of prism duals, triangle faces: (6, 8, 10, 12, ... sides)
- Trapezohedrons: infinite set of antiprism duals, kite faces: (6, 8, 10, 12, ... sides)
- Disphenoids: infinite set of tetrahedra made from congruent non-regular triangles (4 sides)
- "Rolling-pin style dice" (also called "rolling logs"[18]) are the only way to make dice with an odd number of flat faces.[19] They are based on an infinite set of prisms. All the (rectangular) faces they may actually land on are congruent, so they are equally fair. (The other 2 sides of the prism are rounded or capped with a pyramid, designed so that the dice never actually rests on those faces.)
[edit] Probability
| This section does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (August 2008) |
For a single roll of a fair s-sided die, the probability of rolling each value, 1 through s, is exactly 1/s. This is an example of a discrete uniform distribution. For a double roll, however, the total of both rolls is not evenly distributed, but is distributed in a triangular curve. For two six-sided dice, for example, the probability distribution is as follows:
| Sum |
|
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| Probability |
|
|
|
|
|
|
|
|
|
|
|
| Probability (simplified) |
|
|
|
|
|
|
|
|
|
|
|
For three or more die rolls, the curve becomes more bell-shaped with each additional die (according to the central limit theorem). The exact probability distribution Fs,i of a sum of i s-sided dice can be calculated as the repeated convolution of the single-die probability distribution with itself.
where 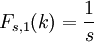 for all
for all  and 0 otherwise.
and 0 otherwise.
A fastest algorithm would adapt the exponentiation by squaring algorithm, using  .
.
For example, in the triangular curve described above,
 |
 |
 |
|
 |
Equivalently, one can calculate the probability using combinations:

The probability of rolling any exact sequence of numbers is simply  . For example, the chance of rolling 1, 2, and 3 in that order with three rolls of a six-sided die is
. For example, the chance of rolling 1, 2, and 3 in that order with three rolls of a six-sided die is  , or
, or  .
.
The article Sampling equiprobably with dice describes the probabilities of sampling with dice from any range.
[edit] Application in role-playing games
| This section does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (August 2008) |
While polyhedral dice had previously been used in teaching basic arithmetic, the fantasy role-playing game Dungeons & Dragons is largely credited with popularizing their use in roleplaying games. Some games use only one type, such as Exalted which uses only ten sided dice, while others use numerous types for different game purposes, such as Dungeons & Dragons, which make use of 20-, 12-, 10-, 8- and 4-sided dice in addition to the traditional 6 sided die. Unlike the common six sided die, these dice often have the numbers engraved on them rather than a series of dots.
Roleplaying games generally use dice to determine the outcome of events, such as the success or failure of actions which are difficult to perform. A player may have to roll dice for combat, skill use, or magic use, amongst other things. This is generally considered fairer than decision by game master fiat, since success and failure are decided randomly based on a flat probability. Games typically determine success as either a total on one or more dice above (Dungeons & Dragons third edition) or below (Call of Cthulhu) a target number, or a certain number of rolls above a certain number (such as 8 or higher on a d10) on one or more dice (White Wolf's World of Darkness series). The player may gain a bonus or penalty due to circumstances or character skill, usually either by a number added to or subtracted from the final result, or by having the player roll extra or fewer dice.
Dice can also be used by a game master for other purposes, such as to randomly generate game content or to make arbitrary decisions. Some games use dice to determine what attributes the player's character has when created, such as how strong he or she is.
In Dungeons & Dragons and some other roleplaying games which use many types of dice, a dice notation is used. For example, a six-sided die is referred to as a d6, while two such dice rolled with the results totaled would be called 2d6. A bonus or penalty applied to the final result is referred to like 2d6+4 or 2d6-2. Games which use only one type of dice rarely require complex dice notation.
A common special case is percentile rolls, referred to in dice notation as 1d100 or 1d%. Since actual hundred-sided dice are large, almost spherical, and difficult to read, percentile rolls are generally handled by rolling two ten-sided dice together, using one as the "tens" and the other as the "units". A roll of ten or zero on either die is taken as a zero, unless both are zeros or tens, in which case this is 100 (rather than zero). To avoid this confusion, sets of percentile dice exist where one is marked in tens (00, 10, 20... up to 90) and the other from 0 to 9.
Dice for role-playing games are usually made of plastic, though infrequently metal, wood, and semi-precious stone dice can be found. Early polyhedral dice from the 1970s and 1980s were made of a soft plastic that would easily wear as the die was used. Typical wear and tear would gradually round the corners and edges of the die until it was unusable. Many early dice were unmarked and players took great care in painting their sets of dice. Some twenty-sided dice of this era were numbered zero through nine twice; half of the numbers had to be painted a contrasting color to signify the "high" faces. Such a die could also double as a ten-sided die by ignoring the distinguishing coloring.
[edit] Use of dice for divination
| This section does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (August 2008) |
Some people believe that dice can be used for divination. Using dice for such a purpose is called cleromancy. A pair of standard 6-sided dice is usual though other forms of polyhedra can be used. Tibetan Buddhists sometimes use this method of divination.
It is uncertain if the Pythagoreans used the "Platonic Solids" as dice, but it is highly likely. They referred to these perfect geometries as "The Dice of the Gods". Julia E. Diggins, writer of String, Straightedge, and Shadow (Viking Press, New York, 1965) writes how the Pythagorean Brotherhood sought to understand the mysteries of the Universe through an understanding of geometry in polyhedra. It is recorded that the dodecahedron (12 sided platonic solid) was discovered by Pythagoras. (Guthrie: The Pythagorean Sourcebook)
Astrological dice are a specialized set of three 12-sided dice for divination, using the concepts of astrology and containing astrological symbols for the planets, the zodiac signs and the astrological houses. The first die represents planets, the Sun, the Moon, and two nodes (North Node and South Node). The second die represents the 12 zodiac signs, and the third represents the 12 houses. In simplified terms, the planets, etc. could represent the 'actor'; the zodiac signs could represent the 'role' being played by the actor; and the house could represent the 'scene' in which the actor plays.
Rune dice are a specialized set of dice for divination (runecasting), using the symbols of the runes printed on the dice.
An icosahedron is used to provide the answers of a Magic 8-Ball, which is conventionally used to provide advice on yes-or-no questions.
[edit] See also
[edit] References
- ^ AskOxford: die2
- ^ Chinese Dice from the Elliott Avedon Museum & Archive of Games
- ^ Standard Dice from dice-play
- ^ gotinker.com, gotinker.com Project site
- ^ RANDOM.ORG, RANDOM.ORG Random number generation
- ^ Lowie, Robert H. (2007) [1940]. An Introduction To Cultural Anthropology. Masterson Press. p. 162. ISBN 1406717657.
- ^ Nejat, Karen Rhea Nemet. (1998). Daily Life in Ancient Mesopotamia. Connecticut: Greenwood Publishing Group. p. 165. ISBN 0313294976
- ^ a b c Brown, W.N. (1964). "The Indian Games of Pachisi, Chaupar, and Chausar". Expedition, 32-35. University of Pennsylvania Museum of Archaeology and Anthropology. 32 (35).
- ^ Possehl, Gregory. "Meluhha". In: J. Reade (ed.) The Indian Ocean in Antiquity. London: Kegan Paul Intl. 1996a, 133–208
- ^ Basham, A. L. (2001) [1967]. The Wonder That was India. Third revised edition. New Delhi: Rupa & co. pp. 207-208 ISBN 0283992573
- ^ Ṛg Veda, Book 10, 34
- ^ Atharva Veda 2.3; 4.38; 6.118; 7.52; 7.109
- ^ "Backgammon". Medieval Islamic Civilization: An Encyclopedia Volume 1, A-K index. Edited by Meri, Josef W (2006). London: Routledge. p. 88. ISBN 0415966906
- ^ http://www.foxnews.com/story/0,2933,253221,00.html FOX News: 5,000-Year-Old Artificial Eye Found on Iran-Afghan Border, Tuesday, February 20, 2007
- ^ http://www.charityadvantage.com/afghan_communicatorNKFPKG/GoldenEye.doc
- ^ AskOxford: ace
- ^ Thompson, Clive (December 2, 2003). "Ancient Roman dungeonmastering". Collision Detection. http://www.collisiondetection.net/mt/archives/2003/12/ancient_roman_d.html. Retrieved on 2006-06-26.
- ^ The International Bone Rollers' Guild
- ^ Properties of Dice
- Persi Diaconis and Joseph B. Keller. "Fair Dice". The American Mathematical Monthly, 96(4):337-339, 1989. (Discussion of dice that are fair "by symmetry" and "by continuity".)
- Bias and Runs in Dice Throwing and Recording: A Few Million Throws. G. R. Iverson. W. H. Longcour, et al. Psychometrika, Vol. 36, No. 1, March 1971
- Knizia, Reiner (1999). Dice Games Properly Explained. Elliot Right Way Books. ISBN 0-7160-2112-9.
[edit] External links
| Wikimedia Commons has media related to: Dice |
- Eric W. Weisstein, Dice at MathWorld. Analysis of dice probabilities, also features Uspenski's work on rolling multiple dice.
- mathematically "Fair Dice"
- Fair Dice is an illustrated Math Games column about all the possible fair dice, and the mathematical reasons why other shapes are not fair.
- a complete list of all possible Fair Dice which has nice illustrations
- "Properties of Dice" describes all solids that make for provably fair dice, and gives more details about all possible Fair Dice
- World's Largest Dice Collection Links, Photos, Information about dice
- Computer Simulation of Irregular Dice
- A Pair Of Dice Which Never Roll 7
- A Brief History of Dice (in Dungeons & Dragons games)
- The Dicer – Nice virtual hexahedron dice machine.
- The Dice Font - Easily add dice to any of your documents
This article incorporates text from the Encyclopædia Britannica Eleventh Edition, a publication now in the public domain.