!enciclopedia %5Bwikipedia_article%5D *edward.lorenz :inglese _now about bfly biology bit200w07 blog boredom butterfly butterflyeffect chaos computing cool effect learning math philosophy physics science sociology theory thesis timetravel web

My tags:

From Wikipedia, the free encyclopedia

The butterfly effect is a phrase that encapsulates the more technical notion of sensitive dependence on initial conditions in chaos theory. Small variations of the initial condition of a dynamical system may produce large variations in the long term behavior of the system. This is sometimes presented as esoteric behavior, but can be exhibited by very simple systems: for example, a ball placed at the crest of a hill might roll into any of several valleys depending on slight differences in initial position.

It is a common subject in fiction when presenting scenarios involving time travel and with "what if" scenarios where one storyline diverges at the moment of a seemingly minor event resulting in two significantly different outcomes.

Contents 1 Theory 2 Origin of the concept and the term 3 Illustration 4 Mathematical definition 5 Appearances in popular culture 6 See also 7 References 8 Further reading 9 External links

[edit] Theory

Recurrence, the approximate return of a system towards its initial conditions, together with sensitive dependence on initial conditions are the two main ingredients for chaotic motion. They have the practical consequence of making complex systems, such as the weather, difficult to predict past a certain time range (approximately a week in the case of weather), since it is impossible to measure the starting atmospheric conditions completely accurately.

[edit] Origin of the concept and the term

The term "butterfly effect" itself is related to the work of Edward Lorenz, and is based in Chaos Theory and sensitive dependence on initial conditions, first described in the literature by Jacques Hadamard in 1890^[1] and popularized by Pierre Duhem's 1906 book. The idea that one butterfly could eventually have a far-reaching ripple effect on subsequent historic events seems first to have appeared in a 1952 short story by Ray Bradbury about time travel (see Literature and print here) although Lorenz made the term popular. In 1961, Lorenz was using a numerical computer model to rerun a weather prediction, when, as a shortcut on a number in the sequence, he entered the decimal .506 instead of entering the full .506127 the computer would hold. The result was a completely different weather scenario.^[2] Lorenz published his findings in a 1963 paper for the New York Academy of Sciences noting that "One meteorologist remarked that if the theory were correct, one flap of a seagull's wings could change the course of weather forever." Later speeches and papers by Lorenz used the more poetic butterfly. According to Lorenz, upon failing to provide a title for a talk he was to present at the 139th meeting of the American Association for the Advancement of Science in 1972, Philip Merilees concocted Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas as a title.

Although a butterfly flapping its wings has remained constant in the expression of this concept, the location of the butterfly, the consequences, and the location of the consequences have varied widely.^[3]

The phrase refers to the idea that a butterfly's wings might create tiny changes in the atmosphere that may ultimately alter the path of a tornado or delay, accelerate or even prevent the occurrence of a tornado in a certain location. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale alterations of events. Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different. While the butterfly does not cause the tornado, the flap of its wings is an essential part of the initial conditions resulting in a tornado.

Chapter four of F. Scott Fitzgerald's story "Winter Dreams" contains the following sentence:

"[The house] was sturdy to accentuate [Judy's] slightness - as if to show what a breeze could be generated by a butterfly's wing."

[edit] Illustration

The butterfly effect in the Lorenz attractor
time 0 ≤ t ≤ 30 (larger)		z coordinate (larger)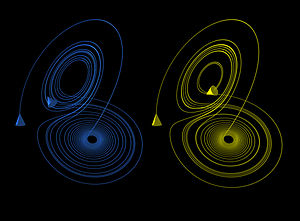
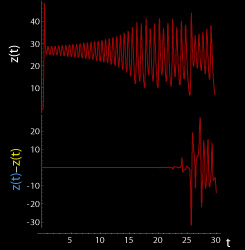
These figures show two segments of the three-dimensional evolution of two trajectories (one in blue, the other in yellow) for the same period of time in the Lorenz attractor starting at two initial points that differ only by 10-5 in the x-coordinate. Initially, the two trajectories seem coincident, as indicated by the small difference between the z coordinate of the blue and yellow trajectories, but for t > 23 the difference is as large as the value of the trajectory. The final position of the cones indicates that the two trajectories are no longer coincident at t=30.
A Java animation of the Lorenz attractor shows the continuous evolution.

[edit] Mathematical definition

A dynamical system with evolution map f^t displays sensitive dependence on initial conditions if points arbitrarily close become separate with increasing t. If M is the state space for the map f^t, then f^t displays sensitive dependence to initial conditions if there is a δ>0 such that for every point x∈M and any neighborhood N containing x there exist a point y from that neighborhood N and a time τ such that the distance

The definition does not require that all points from a neighborhood separate from the base point x.

[edit] Appearances in popular culture

The term is sometimes used in popular media dealing with the idea of time travel, usually inaccurately. Most time travel depictions simply fail to address butterfly effects. According to the actual theory, if history could be "changed" at all (so that one is not invoking something like the Novikov self-consistency principle which would ensure a fixed self-consistent timeline), the mere presence of the time travelers in the past would be enough to change short-term events (such as the weather) and would also have an unpredictable impact on the distant future. Therefore, no one who travels into the past could ever return to the same version of reality he or she had come from and could have therefore not been able to travel back in time in the first place, which would create a phenomenon known as a time paradox.^{[citation needed]}

[edit] See also

• Cascading failure
• Causality
• Chain reaction
• Determinism
• Domino effect
• Dynamical systems
• Fractal
• Snowball effect

[edit] References

[edit] Further reading

• Robert L. Devaney (2003). Introduction to Chaotic Dynamical Systems. Westview Press. ISBN 0-8133-4085-3. 
• Robert C. Hilborn (2004). "Sea gulls, butterflies, and grasshoppers: A brief history of the butterfly effect in nonlinear dynamics". American Journal of Physics 72: 425–427. doi:10.1119/1.1636492. 

[edit] External links

• The meaning of the butterfly: Why pop culture loves the 'butterfly effect,' and gets it totally wrong, Peter Dizikes, Boston Globe, June 8, 2008
• From butterfly wings to single e-mail (Cornell University)
• New England Complex Systems Institute - Concepts: Butterfly Effect
• The Chaos Hypertextbook. An introductory primer on chaos and fractals.
• Eric W. Weisstein, Butterfly Effect at MathWorld.