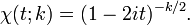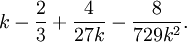Chi-square distribution
From Wikipedia, the free encyclopedia
Probability density function |
|
Cumulative distribution function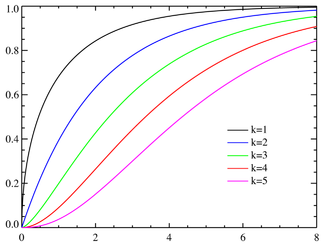 |
|
| Parameters |  degrees of freedom degrees of freedom |
|---|---|
| Support |  |
| Probability density function (pdf) | 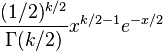 |
| Cumulative distribution function (cdf) |  |
| Mean |  |
| Median | approximately  |
| Mode | 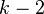 if if  |
| Variance | 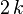 |
| Skewness |  |
| Excess kurtosis | 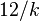 |
| Entropy |  |
| Moment-generating function (mgf) |  for for  |
| Characteristic function | 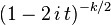 |
In probability theory and statistics, the chi-square distribution (also chi-squared or χ2 distribution) is one of the most widely used theoretical probability distributions in inferential statistics, e.g., in statistical significance tests.[1][2][3][4] It is useful because, under reasonable assumptions, easily calculated quantities can be proven to have distributions that approximate to the chi-square distribution if the null hypothesis is true.
The best-known situations in which the chi-square distribution are used are the common chi-square tests for goodness of fit of an observed distribution to a theoretical one, and of the independence of two criteria of classification of qualitative data. Many other statistical tests also lead to a use of this distribution, like Friedman's analysis of variance by ranks.
Contents |
[edit] Definition
If Xi are k independent, normally distributed random variables with mean 0 and variance 1, then the random variable
is distributed according to the chi-square distribution with k degrees of freedom. This is usually written
The chi-square distribution has one parameter: k - a positive integer that specifies the number of degrees of freedom (i.e. the number of Xi)
The chi-square distribution is a special case of the gamma distribution.
[edit] Characteristics
[edit] Probability density function
A probability density function of the chi-square distribution is
where Γ denotes the Gamma function, which has closed-form values at the half-integers.
[edit] Cumulative distribution function
Its cumulative distribution function is:
where γ(k,z) is the lower incomplete Gamma function and P(k,z) is the regularized Gamma function.
Tables of this distribution — usually in its cumulative form — are widely available and the function is included in many spreadsheets and all statistical packages.
[edit] Characteristic function
The characteristic function of the Chi-square distribution is [5]
[edit] Expected value and variance
If  then the mean is given by
then the mean is given by
and the variance is given by
[edit] Median
The median of  is given approximately by
is given approximately by
[edit] Information entropy
The information entropy is given by
where ψ(x) is the Digamma function.
[edit] Noncentral moments
The moments about zero of a chi-square distribution with k degrees of freedom are given by[6][7]
[edit] Derivation of the pdf for one degree of freedom
Let random variable Y be defined as Y = X2 where X has normal distribution with mean 0 and variance 1 (that is X ~ N(0,1)).
Then if  and if
and if 
Then  .
.
[edit] Related distributions and properties
The chi-square distribution has numerous applications in inferential statistics, for instance in chi-square tests and in estimating variances. It enters the problem of estimating the mean of a normally distributed population and the problem of estimating the slope of a regression line via its role in Student's t-distribution. It enters all analysis of variance problems via its role in the F-distribution, which is the distribution of the ratio of two independent chi-squared random variables divided by their respective degrees of freedom.
- If
 , then as k tends to infinity, the distribution of
, then as k tends to infinity, the distribution of  tends to a standard normal distribution: see asymptotic distribution. This follows directly from the definition of the chi-squared distribution, the central limit theorem, and the fact that the mean and variance of
tends to a standard normal distribution: see asymptotic distribution. This follows directly from the definition of the chi-squared distribution, the central limit theorem, and the fact that the mean and variance of  are 1 and 2 respectively. However, convergence is slow as the skewness is
are 1 and 2 respectively. However, convergence is slow as the skewness is 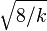 and the excess kurtosis is 12 / k.
and the excess kurtosis is 12 / k. - If
 then
then 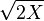 is approximately normally distributed with mean
is approximately normally distributed with mean  and unit variance (result credited to R. A. Fisher).
and unit variance (result credited to R. A. Fisher). - If
 then
then ![\sqrt[3]{X/k}](http://upload.wikimedia.org/math/c/c/f/ccfd20697974afc563a4a0c8c9362a38.png) is approximately normally distributed with mean 1 − 2 / (9k) and variance 2 / (9k) (Wilson and Hilferty,1931)
is approximately normally distributed with mean 1 − 2 / (9k) and variance 2 / (9k) (Wilson and Hilferty,1931)  is an exponential distribution if
is an exponential distribution if 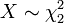 (with 2 degrees of freedom).
(with 2 degrees of freedom). is a chi-square distribution if
is a chi-square distribution if  for
for  independent that are normally distributed.
independent that are normally distributed.- If
![\boldsymbol{z}'=[Z_1,Z_2,\cdots,Z_n]](http://upload.wikimedia.org/math/6/8/c/68c807c69169bc48af273f2c4a2d2da5.png) , where the Zis are independent Normal(0,σ2) random variables or
, where the Zis are independent Normal(0,σ2) random variables or  and
and  is an
is an 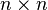 idempotent matrix with rank n − k then the quadratic form
idempotent matrix with rank n − k then the quadratic form  .
. - If the
 have nonzero means, then
have nonzero means, then 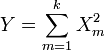 is drawn from a noncentral chi-square distribution.
is drawn from a noncentral chi-square distribution. - The chi-square distribution
 is a special case of the gamma distribution, in that
is a special case of the gamma distribution, in that  .
.  is an F-distribution if
is an F-distribution if  where
where 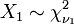 and
and  are independent with their respective degrees of freedom.
are independent with their respective degrees of freedom. is a chi-square distribution if
is a chi-square distribution if  where
where  are independent and
are independent and  .
.- if X is chi-square distributed, then
 is chi distributed.
is chi distributed. - in particular, if
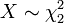 (chi-square with 2 degrees of freedom), then
(chi-square with 2 degrees of freedom), then  is Rayleigh distributed.
is Rayleigh distributed. - if
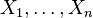 are i.i.d. N(μ,σ2) random variables, then
are i.i.d. N(μ,σ2) random variables, then 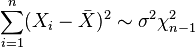 where
where  .
. - if
 , then
, then 
- The box below shows probability distributions with name starting with chi for some statistics based on
 independent random variables:
independent random variables:
| Name | Statistic |
|---|---|
| chi-square distribution |  |
| noncentral chi-square distribution | 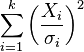 |
| chi distribution | 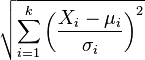 |
| noncentral chi distribution |  |
[edit] See also
- Cochran's theorem
- Inverse-chi-square distribution
- Degrees of freedom (statistics)
- Fisher's method for combining independent tests of significance
- Noncentral chi-square distribution
- Normal distribution
- Wishart distribution
- High-dimensional space
[edit] References
- ^ Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 26", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, ISBN 0-486-61272-4.
- ^ NIST (2006). Engineering Statistics Handbook - Chi-Square Distribution
- ^ Jonhson, N.L.; S. Kotz, , N. Balakrishnan (1994). Continuous Univariate Distributions (Second Ed., Vol. 1, Chapter 18). John Willey and Sons. ISBN 0-471-58495-9.
- ^ Mood, Alexander; Franklin A. Graybill, Duane C. Boes (1974). Introduction to the Theory of Statistics (Third Edition, p. 241-246). McGraw-Hill. ISBN 0-07-042864-6.
- ^ M.A. Sanders. "Characteristic function of the central chi-square distribution". http://www.planetmathematics.com/CentralChiDistr.pdf. Retrieved on 2009-03-06.
- ^ Chi-square distribution, from MathWorld, retrieved Feb. 11, 2009
- ^ M. K. Simon, Probability Distributions Involving Gaussian Random Variables, New York: Springer, 2002, eq. (2.35), ISBN 978-0-387-34657-1
[edit] External links
- Comparison of noncentral and central distributions Density plot, critical value, cumulative probability, etc., online calculator based on R embedded in Mediawiki.
- Course notes on Chi-Square Goodness of Fit Testing from Yale University Stats 101 class. Example includes hypothesis testing and parameter estimation.
- On-line calculator for the significance of chi-square, in Richard Lowry's statistical website at Vassar College.
- Distribution Calculator Calculates probabilities and critical values for normal, t-, chi2- and F-distribution
- Chi-Square Calculator for critical values of Chi-Square in R. Webster West's applet website at University of South Carolina
- Chi-Square Calculator from GraphPad
- Table of Chi-squared distribution
- Mathematica demonstration showing the chi-squared sampling distribution of various statistics, e.g. Σx², for a normal population
- Simple algorithm for approximating cdf and inverse cdf for the chi-square distribution with a pocket calculator
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||