Association rule learning

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In data mining, association rule learning is a popular and well researched method for discovering interesting relations between variables in large databases. Piatetsky-Shapiro [1] describes analyzing and presenting strong rules discovered in databases using different measures of interestingness. Based on the concept of strong rules, Agrawal et al. [2] introduced association rules for discovering regularities between products in large scale transaction data recorded by point-of-sale (POS) systems in supermarkets. For example, the rule \{onions, potatoes\} \Rightarrow \{beef\} found in the sales data of a supermarket would indicate that if a customer buys onions and potatoes together, he or she is likely to also buy beef. Such information can be used as the basis for decisions about marketing activities such as, e.g., promotional pricing or product placements. In addition to the above example from market basket analysis association rules are employed today in many application areas including Web usage mining, intrusion detection and bioinformatics.

Contents

[edit] Definition

Following the original definition by Agrawal et al. [2] the problem of association rule mining is defined as: Let I=\{i_1, i_2,\ldots,i_n\} be a set of n binary attributes called items. Let D = \{t_1, t_2, \ldots, t_m\} be a set of transactions called the database. Each transaction in D has a unique transaction ID and contains a subset of the items in I. A rule is defined as an implication of the form 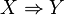X \Rightarrow Y where X, Y \subseteq I and X \cap Y = \emptyset. The sets of items (for short itemsets) X and Y are called antecedent (left-hand-side or LHS) and consequent (right-hand-side or RHS) of the rule.

Example data base with 4 items and 5 transactions
transaction ID milk bread butter beer
1 1 1 0 0
2 0 1 1 0
3 0 0 0 1
4 1 1 1 0
5 0 1 0 0

To illustrate the concepts, we use a small example from the supermarket domain. The set of items is I = {milk,bread,butter,beer} and a small database containing the items (1 codes presence and 0 absence of an item in a transaction) is shown in the table to the right. An example rule for the supermarket could be \{\mathrm{milk, bread}\} \Rightarrow \{\mathrm{butter}\} meaning that if milk and bread is bought, customers also buy butter.

Note: this example is extremely small. In practical applications, a rule needs a support of several hundred itemsets before it can be considered statistically significant, and datasets often contain thousands or millions of itemsets.

To select interesting rules from the set of all possible rules, constraints on various measures of significance and interest can be used. The best-known constraints are minimum thresholds on support and confidence. The support supp(X) of an itemset X is defined as the proportion of transactions in the data set which contain the itemset. In the example database, the itemset {milk,bread} has a support of 2 / 5 = 0.4 since it occurs in 40% of all transactions (2 out of 5 transactions).

The confidence of a rule is defined \mathrm{conf}(X\Rightarrow Y) = \mathrm{supp}(X \cup Y) / \mathrm{supp}(X). For example, the rule \{\mathrm{milk, bread}\} \Rightarrow \{\mathrm{butter}\} has a confidence of 0.2 / 0.4 = 0.5 in the database, which means that for 50% of the transactions containing milk and bread the rule is correct. Confidence can be interpreted as an estimate of the probability P(Y | X), the probability of finding the RHS of the rule in transactions under the condition that these transactions also contain the LHS [3].

The lift of a rule is defined as \mathrm{lift}(X\Rightarrow Y) = \frac{ \mathrm{supp}(X \cup Y)}{ \mathrm{supp}(Y) * \mathrm{supp}(X) } or the ratio of the observed confidence to that expected by chance. The rule \{\mathrm{milk, bread}\} \Rightarrow \{\mathrm{butter}\} has a lift of \frac{0.2}{0.4*0.4} = 1.25 .

The conviction of a rule is defined as \mathrm{conv}(X\Rightarrow Y) =\frac{ 1 - \mathrm{supp}(Y) }{ 1 - \mathrm{conf}(X\Rightarrow Y)}. The rule \{\mathrm{milk, bread}\} \Rightarrow \{\mathrm{butter}\} has a conviction of \frac{1 - 0.4}{1 - .5} = 1.2 , and be interpreted as the ratio of the expected frequency that X occurs without Y (that is to say, the frequency that the rule makes an incorrect prediction) if X and Y were independent divided by the observed frequency of incorrect predictions. In this example, the conviction value of 1.2 shows that the rule \{\mathrm{milk, bread}\} \Rightarrow \{\mathrm{butter}\} would be incorrect 20% more often (1.2 times as often) if the association between X and Y was purely random chance.

Association rules are required to satisfy a user-specified minimum support and a user-specified minimum confidence at the same time. To achieve this, association rule generation is a two-step process. First, minimum support is applied to find all frequent itemsets in a database. In a second step, these frequent itemsets and the minimum confidence constraint are used to form rules. While the second step is straight forward, the first step needs more attention.

Finding all frequent itemsets in a database is difficult since it involves searching all possible itemsets (item combinations). The set of possible itemsets is the power set over I and has size 2n − 1 (excluding the empty set which is not a valid itemset). Although the size of the powerset grows exponentially in the number of items n in I, efficient search is possible using the downward-closure property of support [2](also called anti-monotonicity[4]) which guarantees that for a frequent itemset also all its subsets are frequent and thus for an infrequent itemset, all its supersets must be infrequent. Exploiting this property, efficient algorithms (e.g., Apriori [5] and Eclat [6]) can find all frequent itemsets.

[edit] History

The concept of association rules was popularised particularly due by the 1993 article of Aggrawal [2], which has as of March 2008 acquired more than 6000 citations according to Google Scholar and is thus one of the most cited papers in the datamining field. However, what is now called "association rules" appears already in the 1966 paper [7] on GUHA, a general data mining method developed by Petr Hájek et al. [8].

[edit] Alternative Measures of Interestingness

Next to confidence also other measures of interestingness for rules were proposed. Some popular measures are:

  • All-confidence [9]
  • Collective strength [10]
  • Lift (originally called interest) [11]

A definition of these measures can be found here. Several more measures are presented and compared by Tan et al.[13]

[edit] Algorithms

Many algorithms for generating association rules were presented over time.

Some well known algorithms are Apriori, Eclat and FP-Growth, but they only do half the job, since they are algorithms for mining frequent itemsets. Another step need to be done after to generate rules from frequent itemsets found in a database.

[edit] Apriori algorithm

Main article: Apriori algorithm

Apriori[5] is the best-known algorithm to mine association rules. It uses a breadth-first search strategy to counting the support of itemsets and uses a candidate generation function which exploits the downward closure property of support.

[edit] Eclat algorithm

Eclat[6] is a depth-first search algorithm using set intersection.

[edit] FP-Growth algorithm

FP-growth (frequent pattern growth)[14] uses an extended prefix-tree (FP-tree) structure to store the database in a compressed form. FP-growth adopts a divide-and-conquer approach to decompose both the mining tasks and the databases. It uses a pattern fragment growth method to avoid the costly process of candidate generation and testing used by Apriori.

[edit] One-attribute-rule

The one-attribute-rule, or OneR, is an algorithm for finding association rules. According to Ross, very simple association rules, involving just one attribute in the condition part, often work well in practice with real-world data.[15]. The idea of the OneR (one-attribute-rule) algorithm is to find the one attribute to use to classify a novel datapoint that makes fewest prediction errors.

For example, to classify a car you haven't seen before, you might apply the following rule: If Fast Then Sportscar, as opposed to a rule with multiple attributes in the condition: If Fast And Softtop And Red Then Sportscar.

The algorithm is as follows:

  For each attribute A:
    For each value V of that attribute, create a rule:
      1. count how often each class appears
      2. find the most frequent class, c
      3. make a rule "if A=V then C=c"
    Calculate the error rate of this rule
  Pick the attribute whose rules produce the lowest error rate

[edit] Zero-attribute-rule

The zero-attribute-rule, or ZeroR, does not involved any attribute in the condition part, and always returns the most frequent class in the training set. This algorithm is frequently used to measure the classification success of other algorithms.

[edit] Lore

A famous story about association rule mining is the "beer and diaper" story. A purported survey of behavior of supermarket shoppers discovered that customers (presumably young men) who buy diapers tend also to buy beer. This anecdote became popular as an example of how unexpected association rules might be found from everyday data. [See http://www.dssresources.com/newsletters/66.php]

[edit] GUHA procedure ASSOC

GUHA is a general method for exploratory data analysis that has theoretical foundations in observational calculi [16]. The ASSOC procedure [17] is a GUHA method which mines for generalized association rules using fast bitstrings operations. The association rules mined by this method are more general than those output by apriori, for example "items" can be connected both with conjunction and disjunctions and the relation between antecedent and consequent of the rule is not restricted to setting minimum support and confidence as in apriori: an arbitrary combination of supported interest measures can be used.

[edit] Other types of Association Mining

Contrast set learning is a form of associative learning. Contrast set learners use rules that differ meaningfully in their distribution across subsets[18].

Weighted class learning is another form of associative learning in which weight may be assigned to classes to give focus to a particular issue of concern for the consumer of the data mining results.

K-optimal pattern discovery provides an alternative to the standard approach to association rule learning that requires that each pattern appear frequently in the data.

Mining frequent sequences uses support to find sequences in temporal data[19].

[edit] External links

[edit] Bibliographies

[edit] Implementations

[edit] See also

[edit] References

  1. ^ Piatetsky-Shapiro, G. (1991), Discovery, analysis, and presentation of strong rules, in G. Piatetsky-Shapiro & W. J. Frawley, eds, ‘Knowledge Discovery in Databases’, AAAI/MIT Press, Cambridge, MA.
  2. ^ a b c d R. Agrawal; T. Imielinski; A. Swami: Mining Association Rules Between Sets of Items in Large Databases", SIGMOD Conference 1993: 207-216
  3. ^ Jochen Hipp, Ulrich Güntzer, and Gholamreza Nakhaeizadeh. Algorithms for association rule mining - A general survey and comparison. SIGKDD Explorations, 2(2):1-58, 2000.
  4. ^ Jian Pei, Jiawei Han, and Laks V.S. Lakshmanan. Mining frequent itemsets with convertible constraints. In Proceedings of the 17th International Conference on Data Engineering, April 2-6, 2001, Heidelberg, Germany, pages 433-442, 2001.
  5. ^ a b Rakesh Agrawal and Ramakrishnan Srikant. Fast algorithms for mining association rules in large databases. In Jorge B. Bocca, Matthias Jarke, and Carlo Zaniolo, editors, Proceedings of the 20th International Conference on Very Large Data Bases, VLDB, pages 487-499, Santiago, Chile, September 1994.
  6. ^ a b Mohammed J. Zaki. Scalable algorithms for association mining. IEEE Transactions on Knowledge and Data Engineering, 12(3):372-390, May/June 2000.
  7. ^ Hajek P., Havel I., Chytil M.: The GUHA method of automatic hypotheses determination, Computing 1(1966) 293-308.
  8. ^ Petr Hajek, Tomas Feglar, Jan Rauch, David Coufal. The GUHA method, data preprocessing and mining. Database Support for Data Mining Applications, ISBN 978-3-540-22479-2, Springer, 2004
  9. ^ Edward R. Omiecinski. Alternative interest measures for mining associations in databases. IEEE Transactions on Knowledge and Data Engineering, 15(1):57-69, Jan/Feb 2003.
  10. ^ C. C. Aggarwal and P. S. Yu. A new framework for itemset generation. In PODS 98, Symposium on Principles of Database Systems, pages 18-24, Seattle, WA, USA, 1998.
  11. ^ a b Sergey Brin, Rajeev Motwani, Jeffrey D. Ullman, and Shalom Tsur. Dynamic itemset counting and implication rules for market basket data. In SIGMOD 1997, Proceedings ACM SIGMOD International Conference on Management of Data, pages 255-264, Tucson, Arizona, USA, May 1997.
  12. ^ Piatetsky-Shapiro, G., Discovery, analysis, and presentation of strong rules. Knowledge Discovery in Databases, 1991: p. 229-248.
  13. ^ Pang-Ning Tan, Vipin Kumar, and Jaideep Srivastava. Selecting the right objective measure for association analysis. Information Systems, 29(4):293-313, 2004.
  14. ^ Jiawei Han, Jian Pei, Yiwen Yin, and Runying Mao. Mining frequent patterns without candidate generation. Data Mining and Knowledge Discovery 8:53-87, 2004.
  15. ^ Ross, Peter. "OneR: the simplest method". http://www.dcs.napier.ac.uk/~peter/vldb/dm/node8.html. 
  16. ^ J. Rauch, Logical calculi for knowledge discovery in databases. Proceedings of the First European Symposium on Principles of Data Mining and Knowledge Discovery, Springer, 1997, pgs. 47-57.
  17. ^ Hájek, P.; Havránek P (1978). Mechanising Hypothesis Formation – Mathematical Foundations for a General Theory. Springer-Verlag. ISBN 0-7869-1850-8. http://www.cs.cas.cz/hajek/guhabook/. 
  18. ^ T. Menzies, Y. Hu, "Data Mining For Very Busy People." IEEE Computer, October 2003, pgs. 18-25.
  19. ^ M. J. Zaki. (2001). SPADE: An Efficient Algorithm for Mining Frequent Sequences. Machine Learning Journal, 42, 31–60.
Retrieved from "http://en.wikipedia.org/wiki/Association_rule_learning"
Personal tools