Circular buffer
From Wikipedia, the free encyclopedia
A circular buffer or ring buffer is a data structure that uses a single, fixed-size buffer as if it were connected end-to-end. This structure lends itself easily to buffering data streams.
Contents |
[edit] Uses
An example that could possibly use an overwriting circular buffer is with multimedia. If the buffer is used as the bounded buffer in the producer-consumer problem then it is probably desired for the producer (e.g., an audio generator) to overwrite old data if the consumer (e.g., the sound card) is unable to momentarily keep up. Another example is the digital waveguide synthesis method which uses circular buffers to efficiently simulate the sound of vibrating strings or wind instruments.
The "prized" attribute of a circular buffer is that it does not need to have its elements shuffled around when one is consumed. (If a non-circular buffer were used then it would be necessary to shift all elements when one is consumed.) In other words, the circular buffer is well suited as a FIFO buffer while a standard, non-circular buffer is well suited as a LIFO buffer.
[edit] How it works
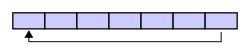
A circular buffer first starts empty and of some predefined length. For example, this is a 7-element buffer:
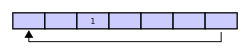
Assume that a 1 is written into the middle of the buffer (exact starting location does not matter in a circular buffer):
Then assume that two more elements are added — 2 & 3 — which get appended after the 1:
If two elements are then removed from the buffer then they come from the end. The two elements removed, in this case, are 1 & 2 leaving the buffer with just a 3:
If the buffer has 7 elements then it is completely full:
A consequence of the circular buffer is that when it is full and a subsequent write is performed, then it starts overwriting the oldest data. In this case, two more elements — A & B — are added and they overwrite then 3 & 4:
Alternatively, the routines that manage the buffer could easily not allow data to be overwritten and return an error or raise an exception. Whether or not data is overwritten is up to the semantics of the buffer routines or the application using the circular buffer.
Finally, if after overwriting elements two elements are removed then what would be returned is not 3 & 4 but 5 & 6 because A & B overwrote the 3 & the 4 yielding the buffer with:
[edit] Circular buffer mechanics
What is not shown in the example above is the mechanics of how the circular buffer is managed.
[edit] Start / End Pointers
Generally, a circular buffer requires three pointers:
- one to the actual buffer in memory
- one to point to the start of valid data
- one to point to the end of valid data
Alternatively, a fixed-length buffer with two integers to keep track of indices can be used in languages that do not have pointers.
Taking a couple of examples from above. (While there are numerous ways to label the pointers and exact semantics can vary, this is one way to do it.)
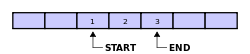
This image shows a partially-full buffer:
This image shows a full buffer with two elements having been overwritten:
What to note about the second one is that after each element is overwritten then the start pointer is incremented as well.
[edit] Difficulties
[edit] Full / Empty Buffer Distinction
Some small disadvantage of relying on pointers or relative indices of the start and end of data is, that in the case the buffer is entirely full, both pointers pointing at the same element:
This is exactly the same situation as when the buffer is empty:
To solve this problem there are a number of solutions:
- Always keep one byte open.
- Use a fill count to distinguish the two cases.
- Use read and write counts to get the fill count from.
- Use absolute indices.
[edit] Always Keep One Byte Open
This simple solution always keeps one byte unallocated. A full buffer has at most (size − 1) bytes. If both pointers are pointing at the same location, the buffer is empty.
The advantages are:
- Very simple and robust.
- You need only the two pointers.
The disadvantages are:
- You can never use the entire buffer.
- If you cannot read over the buffer border, you get a lot of situations where you can only read one element at once.
[edit] Use a Fill Count
The second simplest solution is to use a fill count. The fill count is implemented as an additional variable which keeps the number of readable bytes in the buffer. This variable has to be increased if the write (end) pointer is moved, and to be decreased if the read (start) pointer is moved.
In the situation if both pointers pointing at the same location, you consider the fill count to distinguish if the buffer is empty or full.
- Note: When using semaphores in a Producer-consumer model, the semaphores act as a fill count.
The advantages are:
- Simple.
- Needs only one additional variable.
The disadvantage is:
- You need to keep track of a third variable. This can require complex logic, especially if you are working with different threads.
Alternately, you can replace the second pointer with the fill count and generate the second pointer as required by incrementing the first pointer by the fill count.
The advantages are:
- Simple.
- No additional variables.
The disadvantage is:
- Additional overhead when generating the write pointer.
[edit] Read / Write Counts
Another solution is to keep counts of the number of items written to and read from the circular buffer. Both counts are stored in unsigned integer variables with numerical limits larger than the number of items that can be stored and are allowed to wrap freely from their limit back to zero.
The unsigned difference (write_count - read_count) always yields the number of items placed in the buffer and not yet retrieved. This can indicate that the buffer is empty, partially full, completely full (without waste of a storage location) or in a state of overrun.
The advantage is:
- The source and sink of data can implement independent policies for dealing with a full buffer and overrun while adhering to the rule that only the source of data modifies the write count and only the sink of data modifies the read count. This can result in elegant and robust circular buffer implementations even in multi-threaded environments.
The disadvantage is:
- You need two additional variables.
[edit] Absolute indices
If indices are used instead of pointers, indices can store read/write counts instead of the offset from start of the buffer. This is similar to the above solution, except that there are no separate variables, and relative indices are obtained on the fly by division modulo the buffer's length.
The advantage is:
- No extra variables are needed.
The disadvantages are:
- Every access needs an additional modulo operation.
- If counter wrap is possible, complex logic can be needed if the buffer's length is not a divisor of the counter's capacity.
On binary computers, both of these disadvantages disappear if the buffer's length is a power of two -- at the cost of a constraint on possible buffers lengths.
[edit] Multiple Read Pointers
A little bit more complex are multiple read pointers on the same circular buffer. This is useful if you have n threads, which are reading from the same buffer, but one thread writing to the buffer.
[edit] Chunked Buffer
Much more complex are different chunks of data in the same circular buffer. The writer is not only writing elements to the buffer, it also assigns these elements to chunks.
The reader should not only be able to read from the buffer, it should also get informed about the chunk borders.
Example: The writer is reading data from small files, writing them into the same circular buffer. The reader is reading the data, but needs to know when and which file is starting at a given position.
[edit] Optimization
A circular-buffer implementation may be optimized by mapping the underlying buffer to two contiguous regions of virtual memory. (Naturally, the underlying buffer‘s length must then equal some multiple of the system’s page size.) Reading from and writing to the circular buffer may then be carried out with greater efficiency by means of direct memory access; those accesses which fall beyond the end of the first virtual-memory region will automatically wrap around to the beginning of the underlying buffer. When the read offset is advanced into the second virtual-memory region, both offsets—read and write—are decremented by the length of the underlying buffer.
[edit] Exemplary POSIX Implementation
#include <sys/mman.h> #include <stdlib.h> #include <unistd.h> #define report_exceptional_condition() abort () struct ring_buffer { void *address; unsigned long count_bytes; unsigned long write_offset_bytes; unsigned long read_offset_bytes; }; void ring_buffer_create (struct ring_buffer *buffer, unsigned long order) { char path[] = "/dev/shm/ring-buffer-XXXXXX"; int file_descriptor; void *address; int status; file_descriptor = mkstemp (path); if (file_descriptor < 0) report_exceptional_condition (); status = unlink (path); if (status) report_exceptional_condition (); buffer->count_bytes = 1UL << order; buffer->write_offset_bytes = 0; buffer->read_offset_bytes = 0; status = ftruncate (file_descriptor, buffer->count_bytes); if (status) report_exceptional_condition (); buffer->address = mmap (NULL, buffer->count_bytes << 1, PROT_NONE, MAP_ANONYMOUS | MAP_PRIVATE, -1, 0); if (buffer->address == MAP_FAILED) report_exceptional_condition (); address = mmap (buffer->address, buffer->count_bytes, PROT_READ | PROT_WRITE, MAP_FIXED | MAP_SHARED, file_descriptor, 0); if (address != buffer->address) report_exceptional_condition (); address = mmap (buffer->address + buffer->count_bytes, buffer->count_bytes, PROT_READ | PROT_WRITE, MAP_FIXED | MAP_SHARED, file_descriptor, 0); if (address != buffer->address + buffer->count_bytes) report_exceptional_condition (); status = close (file_descriptor); if (status) report_exceptional_condition (); } void ring_buffer_free (struct ring_buffer *buffer) { int status; status = munmap (buffer->address, buffer->count_bytes << 1); if (status) report_exceptional_condition (); } void * ring_buffer_write_address (struct ring_buffer *buffer) { return buffer->address + buffer->write_offset_bytes; /*** void pointer arithmetic is a constraint violation. ***/ } void ring_buffer_write_advance (struct ring_buffer *buffer, unsigned long count_bytes) { buffer->write_offset_bytes += count_bytes; } void * ring_buffer_read_address (struct ring_buffer *buffer) { return buffer->address + buffer->read_offset_bytes; } void ring_buffer_read_advance (struct ring_buffer *buffer, unsigned long count_bytes) { buffer->read_offset_bytes += count_bytes; if (buffer->read_offset_bytes >= buffer->count_bytes) { buffer->read_offset_bytes -= buffer->count_bytes; buffer->write_offset_bytes -= buffer->count_bytes; } } unsigned long ring_buffer_count_bytes (struct ring_buffer *buffer) { return buffer->write_offset_bytes - buffer->read_offset_bytes; } unsigned long ring_buffer_count_free_bytes (struct ring_buffer *buffer) { return buffer->count_bytes - ring_buffer_count_bytes (buffer); } void ring_buffer_clear (struct ring_buffer *buffer) { buffer->write_offset_bytes = 0; buffer->read_offset_bytes = 0; }