Topology
From Wikipedia, the free encyclopedia

Topology (Greek Τοπολογία, from τόπος, “place”, and λόγος, “study”) is a major area of mathematics that has emerged through the development of concepts from geometry and set theory, such as those of space, dimension, shape, transformation and others.
Ideas that are now classified as topological were expressed as early as 1736, and toward the end of the 19th century a distinct discipline developed, called in Latin the geometria situs (“geometry of place”) or analysis situs (Greek-Latin for “picking apart of place”), and later gaining the modern name of topology. In the middle of the 20th century, this was an important growth area within mathematics.
The word topology is used both for the mathematical discipline and for a family of sets with certain properties that are used to define a topological space, a basic object of topology. Of particular importance are homeomorphisms, which can be defined as continuous functions with a continuous inverse. For instance, the function y = x3 is a homeomorphism of the real line.
Topology includes many subfields. The most basic and traditional division within topology is point-set topology, which establishes the foundational aspects of topology and investigates concepts as compactness and connectedness; algebraic topology, which generally tries to measure degrees of connectivity using algebraic constructs such as homotopy groups and homology; and geometric topology, which primarily studies manifolds and their embeddings (placements) in other manifolds. Some of the most active areas, such as low dimensional topology and graph theory, do not fit neatly in this division.
See also: topology glossary for definitions of some of the terms used in topology and topological space for a more technical treatment of the subject.
Contents |
[edit] History
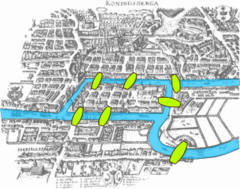
The branch of mathematics now called topology began with the investigation of certain questions in geometry. Euler's 1736 paper on Seven Bridges of Königsberg is regarded as one of the first topological results.
The term "Topologie" was introduced in German in 1847 by Johann Benedict Listing in Vorstudien zur Topologie, Vandenhoeck und Ruprecht, Göttingen, pp. 67, 1848, who had used the word for ten years in correspondence before its first appearance in print. "Topology," its English form, was introduced in 1883 in the journal Nature to distinguish "qualitative geometry from the ordinary geometry in which quantitative relations chiefly are treated". The term topologist in the sense of a specialist in topology was used in 1905 in the magazine Spectator. However, none of these uses corresponds exactly to the modern definition of topology.
Modern topology depends strongly on the ideas of set theory, developed by Georg Cantor in the later part of the 19th century. Cantor, in addition to setting down the basic ideas of set theory, considered point sets in Euclidean space, as part of his study of Fourier series.
Henri Poincaré published Analysis Situs in 1895, introducing the concepts of homotopy and homology, which are now considered part of algebraic topology.
Maurice Fréchet, unifying the work on function spaces of Cantor, Volterra, Arzelà, Hadamard, Ascoli and others, introduced the metric space in 1906. A metric space is now considered a special case of a general topological space. In 1914, Felix Hausdorff coined the term "topological space" and gave the definition for what is now called a Hausdorff space. In current usage, a topological space is a slight generalization of Hausdorff spaces, given in 1922 by Kazimierz Kuratowski.
For further developments, see point-set topology and algebraic topology.
[edit] Elementary introduction
Topological spaces show up naturally in almost every branch of mathematics. This has made topology one of the great unifying ideas of mathematics.
The motivating insight behind topology is that some geometric problems depend not on the exact shape of the objects involved, but rather on the way they are put together. For example, the square and the circle have many properties in common: they are both one dimensional objects (from a topological point of view) and both separate the plane into two parts, the part inside and the part outside.
One of the first papers in topology was the demonstration, by Leonhard Euler, that it was impossible to find a route through the town of Königsberg (now Kaliningrad) that would cross each of its seven bridges exactly once. This result did not depend on the lengths of the bridges, nor on their distance from one another, but only on connectivity properties: which bridges are connected to which islands or riverbanks. This problem, the Seven Bridges of Königsberg, is now a famous problem in introductory mathematics, and led to the branch of mathematics known as graph theory.
Similarly, the hairy ball theorem of algebraic topology says that "one cannot comb the hair flat on a hairy ball without creating a cowlick." This fact is immediately convincing to most people, even though they might not recognize the more formal statement of the theorem, that there is no nonvanishing continuous tangent vector field on the sphere. As with the Bridges of Königsberg, the result does not depend on the exact shape of the sphere; it applies to pear shapes and in fact any kind of smooth blob, as long as it has no holes.
In order to deal with these problems that do not rely on the exact shape of the objects, one must be clear about just what properties these problems do rely on. From this need arises the notion of homeomorphism. The impossibility of crossing each bridge just once applies to any arrangement of bridges homeomorphic to those in Königsberg, and the hairy ball theorem applies to any space homeomorphic to a sphere.
Intuitively two spaces are homeomorphic if one can be deformed into the other without cutting or gluing. A traditional joke is that a topologist can't distinguish a coffee mug from a doughnut, since a sufficiently pliable doughnut could be reshaped to the form of a coffee cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle. A precise definition of homeomorphic, involving a continuous function with a continuous inverse, is necessarily more technical.
Homeomorphism can be considered the most basic topological equivalence. Another is homotopy equivalence. This is harder to describe without getting technical, but the essential notion is that two objects are homotopy equivalent if they both result from "squishing" some larger object.
An introductory exercise is to classify the uppercase letters of the English alphabet according to homeomorphism and homotopy equivalence. The result depends partially on the font used. The figures use a sans-serif font named Myriad. Notice that homotopy equivalence is a rougher relationship than homeomorphism; a homotopy equivalence class can contain several of the homeomorphism classes. The simple case of homotopy equivalence described above can be used here to show two letters are homotopy equivalent, e.g. O fits inside P and the tail of the P can be squished to the "hole" part.
Thus, the homeomorphism classes are: one hole two tails, two holes no tail, no holes, one hole no tail, no holes three tails, a bar with four tails (the "bar" on the K is almost too short to see), one hole one tail, and no holes four tails.
The homotopy classes are larger, because the tails can be squished down to a point. The homotopy classes are: one hole, two holes, and no holes.
To be sure we have classified the letters correctly, we not only need to show that two letters in the same class are equivalent, but that two letters in different classes are not equivalent. In the case of homeomorphism, this can be done by suitably selecting points and showing their removal disconnects the letters differently. For example, X and Y are not homeomorphic because removing the center point of the X leaves four pieces; whatever point in Y corresponds to this point, its removal can leave at most three pieces. The case of homotopy equivalence is harder and requires a more elaborate argument showing an algebraic invariant, such as the fundamental group, is different on the supposedly differing classes.
Letter topology has some practical relevance in stencil typography. The font Braggadocio, for instance, has stencils that are made of one connected piece of material.
[edit] Mathematical definition
Let X be any set and let T be a family of subsets of X. Then T is a topology on X if
- Both the empty set and X are elements of T.
- Any union of arbitrarily many elements of T is an element of T.
- Any intersection of finitely many elements of T is an element of T.
If T is a topology on X, then X together with T is called a topological space.
All sets in T are called open; note that in general not all subsets of X need be in T. A subset of X is said to be closed if its complement is in T (i.e., it is open). A subset of X may be open, closed, both, or neither.
A function or map from one topological space to another is called continuous if the inverse image of any open set is open. If the function maps the real numbers to the real numbers (both spaces with the Standard Topology), then this definition of continuous is equivalent to the definition of continuous in calculus. If a continuous function is one-to-one and onto and if the inverse of the function is also continuous, then the function is called a homeomorphism and the domain of the function is said to be homeomorphic to the range. Another way of saying this is that the function has a natural extension to the topology. If two spaces are homeomorphic, they have identical topological properties, and are considered to be topologically the same. The cube and the sphere are homeomorphic, as are the coffee cup and the doughnut. But the circle is not homeomorphic to the doughnut.
[edit] Topology topics
[edit] Some theorems in general topology
- Every closed interval in R of finite length is compact. More is true: In Rn, a set is compact if and only if it is closed and bounded. (See Heine-Borel theorem).
- Every continuous image of a compact space is compact.
- Tychonoff's theorem: The (arbitrary) product of compact spaces is compact.
- A compact subspace of a Hausdorff space is closed.
- Every continuous bijection from a compact space to a Hausdorff space is necessarily a homeomorphism.
- Every sequence of points in a compact metric space has a convergent subsequence.
- Every interval in R is connected.
- Every compact m-manifold can be embedded in some Euclidean space Rn.
- The continuous image of a connected space is connected.
- A metric space is Hausdorff, also normal and paracompact.
- The metrization theorems provide necessary and sufficient conditions for a topology to come from a metric.
- The Tietze extension theorem: In a normal space, every continuous real-valued function defined on a closed subspace can be extended to a continuous map defined on the whole space.
- Any open subspace of a Baire space is itself a Baire space.
- The Baire category theorem: If X is a complete metric space or a locally compact Hausdorff space, then the interior of every union of countably many nowhere dense sets is empty.
- On a paracompact Hausdorff space every open cover admits a partition of unity subordinate to the cover.
- Every path-connected, locally path-connected and semi-locally simply connected space has a universal cover.
General topology also has some surprising connections to other areas of mathematics. For example:
- in number theory, Furstenberg's proof of the infinitude of primes.
[edit] Some useful notions from algebraic topology
See also list of algebraic topology topics.
- Homology and cohomology: Betti numbers, Euler characteristic, degree of a continuous mapping.
- Operations: cup product, Massey product
- Intuitively-attractive applications: Brouwer fixed-point theorem, Hairy ball theorem, Borsuk-Ulam theorem, Ham sandwich theorem.
- Homotopy groups (including the fundamental group).
- Chern classes, Stiefel-Whitney classes, Pontryagin classes.
[edit] Generalizations
Occasionally, one needs to use the tools of topology but a "set of points" is not available. In pointless topology one considers instead the lattice of open sets as the basic notion of the theory, while Grothendieck topologies are certain structures defined on arbitrary categories which allow the definition of sheaves on those categories, and with that the definition of quite general cohomology theories.
[edit] Topology in art and literature
- Some M. C. Escher works illustrate topological concepts, such as Möbius strips and non-orientable spaces.
[edit] See also
[edit] References
| This article does not cite any references or sources. Please help improve this article by adding citations to reliable sources (ideally, using inline citations). Unsourced material may be challenged and removed. (July 2008) |
[edit] Further reading
- James Munkres (1999). Topology (2nd edition ed.). Prentice Hall. ISBN 0-13-181629-2.
- John L. Kelley (1975). General Topology. Springer-Verlag. ISBN 0-387-90125-6.
- Clifford A. Pickover (2006). The Möbius Strip: Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. Thunder's Mouth Press (Provides a popular introduction to topology and geometry). ISBN 1-56025-826-8.
- Boto von Querenburg (2006). Mengentheoretische Topologie. Heidelberg: Springer-Lehrbuch. ISBN 3-540-67790-9 (German)
- Richeson, David S. (2008) Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press.
[edit] External links
| Wikimedia Commons has media related to: Topology |
| Wikibooks has more on the topic of |
- Elementary Topology: A First Course Viro, Ivanov, Netsvetaev, Kharlamov
- An invitation to Topology Planar Machines' web site
- Geometry and Topology Index, MacTutor History of Mathematics archive
- ODP category
- The Topological Zoo at The Geometry Center
- Topology Atlas
- Topology Course Lecture Notes Aisling McCluskey and Brian McMaster, Topology Atlas
- Topology Glossary
- Moscow 1935: Topology moving towards America, a historical essay by Hassler Whitney.
- "Topologically Speaking", a song about topology.
- "The Use of Topology in Dance", a review of Alvin Ailey's Memoria on ExploreDance.com in which the use of topologies as a way of structuring choreography is discussed.
|
|||||||||||
|
|||||



