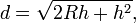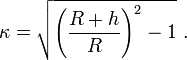Horizon
From Wikipedia, the free encyclopedia

The horizon (Ancient Greek ὁ ὁρίζων, /ho horídzôn/, from ὁρίζειν, "to limit") is the apparent line that separates earth from sky.
More precisely, it is the line that divides all of the directions one can possibly look into two categories: those which intersect the Earth's surface, and those which do not. At many locations, the true horizon is obscured by nearby trees, buildings, mountains and so forth. The resulting intersection of earth and sky is instead described as the visible horizon. When looking at a sea from a shore, the part of the sea closest to the horizon is called the offing.
Contents |
[edit] Appearance and usage
For observers aboard a ship at sea, the true horizon is strikingly apparent. Historically, the distance to the visible horizon has been extremely important as it represented the maximum range of communication and vision before the development of the radio and the telegraph. Even today, when flying an aircraft under Visual Flight Rules, a technique called attitude flying is used to control the aircraft, where the pilot uses the visual relationship between the aircraft's nose and the horizon to control the aircraft. A pilot can also retain his or her spatial orientation by referring to the horizon.
In many contexts, especially perspective drawing, the curvature of the earth is typically disregarded and the horizon is considered the theoretical line to which points on any horizontal plane converge (when projected onto the picture plane) as their distance from the observer increases. Note that, for observers near the ground, the difference between this geometrical horizon (which assumes a perfectly flat, infinite ground plane) and the true horizon (which assumes a spherical Earth surface) is typically imperceptibly small, because of the relative size of the observer.
In astronomy the horizon is the horizontal plane through (the eyes of) the observer. It is the fundamental plane of the horizontal coordinate system, the locus of points which have an altitude of zero degrees. While similar in ways to the geometrical horizon described above, in this context a horizon may be considered to be a plane in space, rather than a line on a picture plane.
[edit] Distance to the horizon
[edit] Approximate formulas
For SI units, the straight line of sight distance d in kilometers to the true horizon on earth is approximately

where h is the height above ground or sea level (in meters) of the eye of the observer. Examples:
- For an observer standing on the ground with h = 1.70 m (average eye-level height), the horizon appears at a distance of 4.7 km.
- For an observer standing on a hill or tower of 100 m in height, the horizon appears at a distance of 36 km.
In the Imperial version of the formula, 13 is replaced by 1.5, h is in feet and d is in miles. Thus:

Examples:
- For observers on the ground with eye-level at h = 5 ft 7 in (5.583 ft), the horizon appears at a distance of 2.89 miles.
- For observers standing on a hill or tower 100 ft in height, the horizon appears at a distance of 12.25 miles.
These formulas may be used when h is much smaller than the radius of the Earth (6371 km), including all views from any mountaintops, airplanes, or even high-altitude balloons. The metric formula is accurate to about 1%; the imperial one is more accurate still.
[edit] Exact formula
The exact formula for distance from the viewpoint to the horizon, applicable even for satellites, is
where R is the radius of the Earth (note: both R and h in this equation must be given in the same units, e.g. kilometers, but any consistent units will work). This exact formula follows directly from the Pythagorean Theorem (a right triangle can be drawn with vertices at the center of the Earth, your eyes, and the point on the horizon. If h is given in meters, h < < R and R is about 6378 km, then the distance in kilometers will be approximately  .
.
Another relationship involves the arc length distance s along the curved surface of the Earth to the bottom of object:
Solving for s gives the formula
The distances d and s are nearly the same when the height of the object is negligible compared to the radius (that is, h<<R).
[edit] Optical adjustments and objects above the horizon
To compute the height of a tower, the mast of a ship or a hilltop visible above the horizon, compute the distance-to-horizon for a hypothetical observer on top of that object, and add it to the real observer's own distance-to-horizon. For example, standing on the ground with h = 1.70 m, the horizon is 4.65 km away. For a tower with a height of 100 m, the horizon distance is 35.7 km. Thus an observer on a beach can see the tower as long as it is not more than 40.35 km away. Conversely, if an observer on a boat (h = 1.7 m) can just see the tops of trees on a nearby shore (h = 10 m), they are probably about 16 km away.
Note that the actual visual horizon is slightly farther away than the calculated visual horizon, due to the atmospheric refraction of light rays. This effect can be taken into account by using a "virtual radius" that is typically about 20% larger than the true radius of the Earth.
[edit] Curvature of the horizon
From a point above the surface the horizon appears slightly bent. There is a basic geometrical relationship between this visual curvature κ, the altitude and the Earth's radius. It is
The curvature is the reciprocal of the curvature angular radius in radians. A curvature of 1 appears as a circle of an angular radius of 45° corresponding to an altitude of approximately 2640 km above the Earth's surface. At an altitude of 10 km (33,000 ft, the typical cruising altitude of an airliner) the mathematical curvature of the horizon is about 0.056, the same curvature of the rim of circle with a radius of 10 metres that is viewed from 56 centimetres. However, the apparent curvature is less than that due to refraction of light in the atmosphere and because the horizon is often masked by high cloud layers that reduce the altitude above the visual surface.
[edit] See also
- Dawn: the time right before sunrise
- Dusk: the time right after sunset, yielding to twilight
- Landscape
- Landscape art
- Aerial landscape art
- Sextant