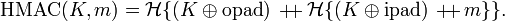@toread algorithm algorithms api authentication captcha criptografia crypto cryptography digest encryption hash hash_function hashing hmac hmac-sha1 internet key legallink md5 message_authentication_code php-image programming protocol research s3 secure security

My tags:

From Wikipedia, the free encyclopedia

In cryptography, a keyed-Hash Message Authentication Code (HMAC or KHMAC), is a type of message authentication code (MAC) calculated using a specific algorithm involving a cryptographic hash function in combination with a secret key. As with any MAC, it may be used to simultaneously verify both the data integrity and the authenticity of a message. Any iterative cryptographic hash function, such as MD5 or SHA-1, may be used in the calculation of an HMAC; the resulting MAC algorithm is termed HMAC-MD5 or HMAC-SHA1 accordingly. The cryptographic strength of the HMAC depends upon the cryptographic strength of the underlying hash function, on the size and quality of the key and the size of the hash output length in bits.

An iterative hash function breaks up a message into blocks of a fixed size and iterates over them with a compression function. For example, MD5 and SHA-1 operate on 512-bit blocks. The size of the output of HMAC is the same as that of the underlying hash function (128 or 160 bits in the case of MD5 or SHA-1, respectively), although it can be truncated if desired. Truncating the hash image reduces the security of the MAC which is bounded above by the birthday attack.

The construction and analysis of HMACs was first published in 1996 by Mihir Bellare, Ran Canetti, and Hugo Krawczyk, who also wrote RFC 2104. FIPS PUB 198 generalizes and standardizes the use of HMACs. HMAC-SHA-1 and HMAC-MD5 are used within the IPsec and TLS protocols.

Contents 1 Definition 2 Implementation 3 Example usage 4 Design principles 5 Security 6 External links 7 References

[edit] Definition

Let be a cryptographic hash function, 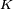be a secret key padded to the right with extra zeros to the block size of the hash function, 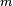be the message to be authenticated, 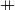denote concatenation, denote exclusive or (XOR), and the outer padding and inner padding 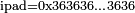be two one-block–long hexadecimal constants. Then 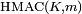is mathematically defined by

[edit] Implementation

The following pseudocode demonstrates how HMAC may be implemented.

function hmac (key, message)
    opad = [0x5c * blocksize] // Where blocksize is that of the underlying hash function
    ipad = [0x36 * blocksize]

    if (length(key) > blocksize) then
        key = hash(key) // keys longer than blocksize are shortened
    end if

    for i from 0 to length(key) - 1 step 1
        ipad[i] = ipad[i] ⊕ key[i] // Where ⊕ is exclusive or (XOR)
        opad[i] = opad[i] ⊕ key[i]
    end for

    return hash(opad ++ hash(ipad ++ message)) // Where ++ is concatenation
end function

[edit] Example usage

A business that suffers from attackers that place fraudulent Internet orders may insist that all its customers deposit a secret key with them. Along with an order, a customer must supply the order's HMAC digest, computed using the customer's symmetric key. The business, knowing the customer's symmetric key, can then verify that the order originated from the stated customer and has not been tampered with.

[edit] Design principles

The design of the HMAC specification was motivated by the existence of attacks on more trivial mechanisms for combining a key with a hash function. For example, one might assume the same security that HMAC provides could be achieved with MAC = H(key ++ message). However this method suffers from a serious flaw, depending on the hash function's implementation, one could add data to the message without knowing the key and obtain a valid MAC. To fix this, one might consider inputting the message length at the beginning, however this too has been found to have weaknesses. Using MAC = H(key ++ message ++ key) is better, however various security papers have suggested vulnerabilities with this approach, even when two different keys are used. No known extensions attacks have been found against the current HMAC specification which is defined as H(key1 ++ H(key2 ++ message)) because the outer application of the hash function masks the intermediate result of the internal hash. The ipad and opad were defined in such a way to have a large hamming distance from each other and so the inner and outer keys will have fewer bits in common.

[edit] Security

The cryptographic strength of the HMAC depends upon the size of the secret key that is used. The most common attack against HMACs is brute force to uncover the secret key. HMACs are not affected by collisions. ^[1]

In "On the Security of HMAC and NMAC Based on HAVAL, MD4, MD5, SHA-0 and SHA-1", by Jongsung Kim, Alex Biryukov, Bart Preneel, Seokhie Hong, claim to have devised: "two new distinguishers of the structure of HMAC, called differential and rectangle distinguishers, and use them to discuss the security of HMAC based on HAVAL, MD4, MD5, SHA-0 and SHA-1. We show how to distinguish HMAC with reduced or full versions of these cryptographic hash functions from a random function or from HMAC with a random function. We also show how to use our differential distinguisher to devise a forgery attack on HMAC. Our distinguishing and forgery attacks can also be mounted on NMAC based on HAVAL, MD4, MD5, SHA-0 and SHA-1. Furthermore, we show that our differential and rectangle distinguishers can lead to second-preimage attacks on HMAC and NMAC.". They go on to claim: "With these distinguishing and forgery attacks we have shown that HMAC with the full versions of 3-pass HAVAL and SHA-0 can be distinguished from HMAC with a random function, and HMAC with the full version of MD4 can be forged. These distinguishing and forgery attacks have also been applied to HMAC based on reduced versions of MD5 and SHA-1. All these attacks do not contradict the security proof of HMAC, but they improve our understanding of the security of HMAC based on existing cryptographic hash functions."

[edit] External links

• FIPS PUB 198, The Keyed-Hash Message Authentication Code
• Python HMAC implementation
• Perl HMAC implementation
• Ruby HMAC implementation
• Design Principles

[edit] References

1. ^ Bruce Schneier (August 2005). "SHA-1 Broken". http://www.schneier.com/blog/archives/2005/02/sha1_broken.html. Retrieved on 2009-1-9. "although it doesn't affect applications such as HMAC where collisions aren't important" 

• Mihir Bellare, Ran Canetti and Hugo Krawczyk, Keying Hash Functions for Message Authentication, CRYPTO 1996, pp1–15 (PS or PDF).
• Mihir Bellare, Ran Canetti and Hugo Krawczyk, Message authentication using hash functions: The HMAC construction, CryptoBytes 2(1), Spring 1996 (PS or PDF).
• Jongsung Kim, Alex Biryukov, Bart Preneel, Seokhie Hong, "On the Security of HMAC and NMAC Based on HAVAL, MD4, MD5, SHA-0 and SHA-1", 2006. (pdf)

v • d • e   Cryptographic hash functions and message authentication codes (MACs) Widely used functions: MD5 | SHA    Other: GOST | HAS-160 | HAVAL | LM hash | MDC-2 | MD2 | MD4 | N-Hash | RadioGatún | RIPEMD | Snefru | Tiger | WHIRLPOOL | crypt(3) DES SHA-3 candidates: CubeHash | Fugue | Grøstl | JH | Keccak | Lane | SANDstorm | MD6 | Skein MAC algorithms: DAA | CBC-MAC | HMAC | OMAC/CMAC | PMAC | UMAC | Poly1305-AES Authenticated encryption modes: CCM | CWC | EAX | GCM | OCB Attacks: Hash collision | Birthday attack | Preimage attack | Rainbow table | Side channel attack | Brute force attack Misc: Avalanche effect | Hash collision | Merkle-Damgård construction   Standardization: CRYPTREC | NESSIE | NIST hash function competition v • d • e   Cryptography History of cryptography · Cryptanalysis · Cryptography portal · Topics in cryptography Symmetric-key algorithm · Block cipher · Stream cipher · Public-key cryptography · Cryptographic hash function · Message authentication code · Random numbers · Steganography