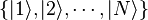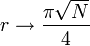Grover's algorithm

From Wikipedia, the free encyclopedia

Grover's algorithm is a quantum algorithm for searching an unsorted database with N entries in O(N^1/2) time and using O(logN) storage space (see big O notation). It was invented by Lov Grover in 1996.

Classically, searching an unsorted database requires a linear search, which is O(N) in time. Grover's algorithm, which takes O(N^1/2) time, is the fastest possible quantum algorithm for searching an unsorted database.^[1] It provides a quadratic speedup, unlike other quantum algorithms, which may provide exponential speedup over their classical counterparts. However, even quadratic speedup is considerable when N is large.

Like many quantum computer algorithms, Grover's algorithm is probabilistic in the sense that it gives the correct answer with high probability. The probability of failure can be decreased by repeating the algorithm. (An example of a deterministic quantum algorithm is the Deutsch-Jozsa algorithm, which produces the correct answer with probability one.)

[edit] Applications

Although the purpose of Grover's algorithm is usually described as "searching a database", it may be more accurate to describe it as "inverting a function". Roughly speaking, if we have a function y=f(x) that can be evaluated on a quantum computer, this algorithm allows us to calculate x when given y. Inverting a function is related to the searching of a database because we could come up with a function that produces a particular value of y if x matches a desired entry in a database, and another value of y for other values of x.

Grover's algorithm can also be used for estimating the mean and median of a set of numbers, and for solving the Collision problem. In addition, it can be used to solve NP-complete problems by performing exhaustive searches over the set of possible solutions. This, while requiring prohibitive space for large input, would result in a considerable speed-up over classical algorithms, though the solution still rests outside polynomial time. The algorithm can be further optimized if there is more than one matching entry and the number of matches is known beforehand.

[edit] Setup

Consider an unsorted database with N entries. The algorithm requires an N-dimensional state space H, which can be supplied by log₂N qubits.

Let us number the database entries by 1, 2,... , N. Choose an observable, Ω, acting on H, with N distinct eigenvalues whose values are all known. Each of the eigenstates of Ω encode one of the entries in the database, in a manner that we will describe. Denote the eigenstates (using bra-ket notation) as

$\{|1\rang, |2\rang, \cdots, |N\rang\}$

and the corresponding eigenvalues by

$\{\lambda_1, \lambda_2, \cdots, \lambda_{N} \}$

We are provided with a unitary operator, U_ω, which acts as a subroutine that compares database entries according to some search criterion. The algorithm does not specify how this subroutine works, but it must be a quantum subroutine that works with superpositions of states. Furthermore, it must act specially on one of the eigenstates, |ω>, which corresponds to the database entry matching the search criterion. To be precise, we require U_ω to have the following effects:

$U_\omega |\omega\rang = - |\omega\rang$

$U_\omega |x\rang = |x\rang \qquad \mbox{for all}\ x \ne \omega$

or

$\langle \omega| \omega\rang =1$ .

$\langle \omega| x \rang =\langle x| \omega\rang =0$ .

Our goal is to identify this eigenstate |ω>, or equivalently the eigenvalue ω, that U_ω acts specially upon.

Also we can write:

$\lang\omega|s\rang =\lang s|\omega\rang = \frac{1}{\sqrt{N}}$ .

$\langle s| s\rang =N\frac{1}{\sqrt{N}}\cdot \frac{1}{\sqrt{N}}=1$ .

$U_\omega |s\rang = (I-2| \omega\rangle \langle \omega|)|s\rang=|s\rang-2| \omega\rangle \langle \omega|s\rang=|s\rang-\frac{2}{\sqrt{N}}|\omega\rangle$ .

$U_s(|s\rang-\frac{2}{\sqrt{N}}|\omega\rangle) = (2 |s\rang \lang s| - I)(|s\rang-\frac{2}{\sqrt{N}}|\omega\rangle)=2 |s\rang \lang s|s\rang-|s\rang-\frac{4}{\sqrt{N}}|s\rang \langle s|\omega\rang+\frac{2}{\sqrt{N}}|\omega\rang=$ .

$=2|s\rang-|s\rang-\frac{4}{\sqrt{N}}\cdot\frac{1}{\sqrt{N}}|s\rang+\frac{2}{\sqrt{N}}|\omega\rang=|s\rang-\frac{4}{N}|s\rang+\frac{2}{\sqrt{N}}|\omega\rang=\frac{N-4}{N}|s\rang+\frac{2}{\sqrt{N}}|\omega\rang$ .

After application of the two operators ( $U ω$ and $U s$ ), the amplitude of the searched-for element increases. And this is one Grover iteration r. N=2ⁿ, n is number of qubits in blank (zero) state.

[edit] Algorithm steps

The steps of Grover's algorithm are as follows:

Initialize the system to the state

$|s\rang = \frac{1}{\sqrt{N}} \sum_{x=1}^{N} |x\rang$
Perform the following "Grover iteration" r(N) times. The function r(N) is described below.
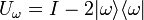1. Apply the operator $U_\omega=I-2| \omega\rangle \langle \omega|$ .
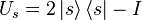2. Apply the operator $U_s = 2 \left|s\right\rangle \left\langle s\right| - I$ .
Perform the measurement Ω. The measurement result will be λ_ω with probability approaching 1 for N>>1. From λ_ω, ω may be obtained.

Our initial state is

$|s\rang = \frac{1}{\sqrt{N}} \sum_{x=1}^{N} |x\rang$

$\lang\omega|s\rang =\lang s|\omega\rang = \frac{1}{\sqrt{N}}$

In geometric terms, there is an angle (π/2 - θ/2) between |ω> and |s>, where θ/2 is given by:

$\cos \left(\frac{\pi}{2} - \frac{\theta}{2} \right) = \frac{1}{\sqrt{N}}$

$\sin \frac{\theta}{2} = \frac{1}{\sqrt{N}}$

The operator U_ω is a reflection at the hyperplane orthogonal to |ω>; for vectors in the plane spanned by |s> and |ω>, it acts as a reflection at the line through |ω^×>. The operator U_s is a reflection at the line through |s>. Therefore, the state vector remains in the plane spanned by |s> and |ω> after each application of U_s and after each application of U_ω, and it is straightforward to check that the operator U_sU_ω of each Grover iteration step rotates the state vector by an angle of θ toward |ω>.

We need to stop when the state vector passes close to |ω>; after this, subsequent iterations rotate the state vector away from |ω>, reducing the probability of obtaining the correct answer. The number of times to iterate is given by r:

$r \rightarrow \frac{\pi \sqrt{N}}{4}$

Furthermore, the probability of obtaining the wrong answer is $O (1 / N)$ , which approaches zero as N increases.

The probability of measuring the correct answer is:

$\sin^2\left( \frac{2r+1}{2} \theta\right) ,$

where r is the (integer) number of Grover iterations, and

$\theta = 2\arccos\left( \sqrt{1-\frac{1}{N}} \right)=2\arcsin \frac{1}{\sqrt{2^n}} .$

[edit] Extensions

If, instead of 1 matching entry, there are k matching entries, the same algorithm works but the number of iterations must be π(N/k)^1/2/4 instead of πN^1/2/4. There are several ways to handle the case if k is unknown. For example, one could run Grover's algorithm several times, with

$\pi \frac{N^{1/2}}{4}, \pi \frac{(N/2)^{1/2}}{4}, \pi \frac{(N/4)^{1/2}}{4}, \ldots$

iterations. For any k, one of iterations will find a matching entry with a sufficiently high probability. The total number of iterations is at most

$\pi \frac{N^{1/2}}{4} \left( 1+ \frac{1}{\sqrt{2}}+\frac{1}{2}+\cdots\right)$

which is still O(N^1/2).

It can be shown that this could be improved. If the number of marked items is k, where k is unknown, there is an algorithm that finds the solution in $O(\frac{N}{k})^{1/2}$ queries. This fact is used in order to solve the collision problem.

[edit] Optimality

It is known that Grover's algorithm is optimal. That is, any algorithm that accesses the database only by using the operator U_ω must apply U_ω at least as many times as Grover's algorithm.^[1] This result is important in understanding the limits of quantum computation. If the Grover's search problem was solvable with log^c N applications of U_ω, that would imply that NP is contained in BQP, by transforming problems in NP into Grover-type search problems. The optimality of Grover's algorithm suggests (but does not prove) that NP is not contained in BQP.

The number of iterations for k matching entries, π(N/k)^1/2/4, is also optimal.

[edit] References

Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212
Grover L.K.: From Schrödinger's equation to quantum search algorithm, American Journal of Physics, 69(7): 769-777, 2001. Pedagogical review of the algorithm and its history.
http://www.bell-labs.com/user/feature/archives/lkgrover/
http://arxiv.org/abs/quant-ph/0301079 Grover's Algorithm: Quantum Database Search
Grover's algorithm on arxiv.org

[edit] Notes

^ ^a ^b Bennett C.H., Bernstein E., Brassard G., Vazirani U., The strengths and weaknesses of quantum computation. SIAM Journal on Computing 26(5): 1510-1523 (1997). Shows the optimality of Grover's algorithm.

[bennett_1997-0] Bennett C.H., Bernstein E., Brassard G., Vazirani U., The strengths and weaknesses of quantum computation. SIAM Journal on Computing 26(5): 1510-1523 (1997). Shows the optimality of Grover's algorithm.

[1]

Grover's algorithm

From Wikipedia, the free encyclopedia

Contents

[edit] Applications

[edit] Setup

[edit] Algorithm steps

[edit] Extensions

[edit] Optimality

[edit] References

[edit] Notes

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages