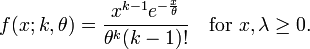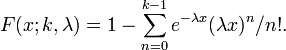Erlang distribution
From Wikipedia, the free encyclopedia
Probability density function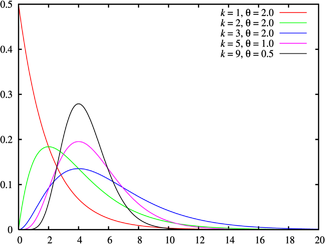 |
|
Cumulative distribution function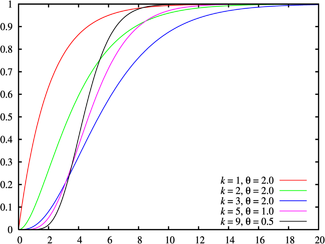 |
|
| Parameters |  shape shape rate (real) rate (real)alt.: 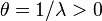 scale (real) scale (real) |
|---|---|
| Support |  |
| Probability density function (pdf) |  |
| Cumulative distribution function (cdf) |  |
| Mean |  |
| Median | no simple closed form |
| Mode | 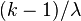 for for 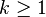 |
| Variance | 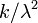 |
| Skewness |  |
| Excess kurtosis |  |
| Entropy |  |
| Moment-generating function (mgf) |  for for 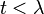 |
| Characteristic function |  |
The Erlang distribution is a continuous probability distribution with wide applicability primarily due to its relation to the exponential and Gamma distributions. The Erlang distribution was developed by A. K. Erlang to examine the number of telephone calls which might be made at the same time to the operators of the switching stations. This work on telephone traffic engineering has been expanded to consider waiting times in queueing systems in general. The distribution is now used in the field of stochastic processes.
Contents |
[edit] Overview
The distribution is a continuous distribution, which has a positive value for all real numbers greater than zero, and is given by two parameters: the shape k, which is a non-negative integer, and the rate λ, which is a non-negative real number. The distribution is sometimes defined using the inverse of the rate parameter, the scale θ.
When the shape parameter k equals 1, the distribution simplifies to the exponential distribution.
The Erlang distribution is a special case of the Gamma distribution where the shape parameter k is an integer. In the Gamma distribution, this parameter is not restricted to the integers.
[edit] Characterization
[edit] Probability density function
The probability density function of the Erlang distribution is
where e is the base of the natural logarithm and ! is the factorial function. The parameter k is called the shape parameter and the parameter λ is called the rate parameter. An alternative, but equivalent, parametrization uses the scale parameter θ which is the reciprocal of the rate parameter (i.e. θ = 1 / λ):
Because of the factorial function in the denominator, the Erlang distribution is only defined when the parameter k is a positive integer. In fact, this distribution is sometimes called the Erlang-k distribution (e.g., an Erlang-2 distribution is an Erlang distribution with k=2). The Gamma distribution generalizes the Erlang by allowing k to be a real, using the gamma function instead of the factorial function.
[edit] Cumulative distribution function
The cumulative distribution function of the Erlang distribution is
where γ() is the lower incomplete gamma function. The CDF may also be expressed as
[edit] Occurrence
[edit] Waiting times
Events which occur independently with some average rate are modeled with a Poisson process. The waiting times between k occurrences of the event are Erlang distributed. (The related question of the number of events in a given amount of time is described by the Poisson distribution.)
The Erlang distribution, which measures the time between incoming calls, can be used in conjunction with the expected duration of incoming calls to produce information about the traffic load measured in Erlang units. This can be used to determine the probability of packet loss or delay, according to various assumptions made about whether blocked calls are aborted (Erlang B formula) or queued until served (Erlang C formula). The Erlang-B and C formulae are still in everyday use for traffic modeling for applications such as the design of call centers.
[edit] Compartment models
The Erlang distribution also occurs as a description of the rate of transition of elements through a system of compartments. Such systems are widely used in biology and ecology. For example, in mathematical epidemiology, an individual may progress at an exponential rate from healthy to carrier and again exponentially from carrier to infectious. The probability of seeing an infectious individual at time t would then be given by Erlang distribution with k=2. Such models have the useful property that the variance in the infectious compartment is large. In a pure exponential model the variance 1 / λ2 - which is often unrealistically small.
[edit] Stochastic processes
The Erlang distribution is the distribution of the sum of k independent identically distributed random variables each having an exponential distribution.
[edit] See also
- Erlang B formula
- Exponential distribution
- Gamma distribution
- Poisson distribution
- Coxian distribution
- Poisson process
- Erlang unit
- Engset calculation
- Phase-type distribution
[edit] External links
- Erlang Distribution
- An Introduction to Erlang B and Erlang C by Ian Angus (PDF Document - Has terms and formulae plus biography)
- Resource Dimensioning Using Erlang-B and Erlang-C
- Erlang-C