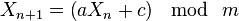Linear congruential generator
From Wikipedia, the free encyclopedia
A linear congruential generator (LCG) represents one of the oldest and best-known pseudorandom number generator algorithms.[1] The theory behind them is easy to understand, and they are easily implemented and fast.
The generator is defined by the recurrence relation:
where Xn is the sequence of pseudorandom values, and
the "modulus"
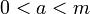the "multiplier"
the "increment" (the special case of c = 0 corresponds to Park–Miller RNG)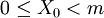
the "seed" or "start value"
are integer constants that specify the generator.
The period of a general LCG is at most m, and for some choices of a much less than that. The LCG will have a full period if and only if:
- 1.
and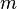 
are relatively prime, - 2.
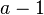is divisible by all prime factors of 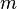, - 3. 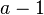is a multiple of 4 if 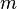is a multiple of 4.[2]
While LCGs are capable of producing decent pseudorandom numbers, this is extremely sensitive to the choice of the coefficients c, m, and a.
Historically, poor choices had led to ineffective implementations of LCGs. A particularly illustrative example of this is RANDU which was widely used in the early 1970s and resulted in many results that are currently in doubt because of the use of this poor LCG [3].
If a linear congruential generator is seeded with a character and then iterated once, the result is a simple classical cipher called an affine cipher; this cipher is easily broken by standard frequency analysis.
Contents |
[edit] LCGs in common use
The most efficient LCGs have an m equal to a power of 2, most often m = 232 or m = 264, because this allows the modulus operation to be computed by merely truncating all but the rightmost 32 or 64 bits. The following table lists the parameters of LCGs in common use, including built-in rand() functions in various compilers.
| Source | m | a | c | output bits of seed in rand() / Random(L) |
|---|---|---|---|---|
| Numerical Recipes | 232 | 1664525 | 1013904223 | |
| Borland C/C++ | 232 | 22695477 | 1 | bits 30..16 in rand(), 30..0 in lrand() |
| glibc (used by GCC) | 232 | 1103515245 | 12345 | bits 30..0 |
| ANSI C: Watcom, Digital Mars, CodeWarrior, IBM VisualAge C/C++ | 232 | 1103515245 | 12345 | bits 30..16 |
| Borland Delphi, Virtual Pascal | 232 | 134775813 | 1 | bits 63..32 of (seed * L) |
| Microsoft Visual/Quick C/C++ | 232 | 214013 | 2531011 | bits 30..16 |
| Apple CarbonLib | 231 − 1 | 16807 | 0 | see Park–Miller RNG |
[edit] Advantages and disadvantages of LCGs
LCGs should not be used for applications where high-quality randomness is critical.
For example, it is not suitable for a Monte Carlo simulation because of the serial correlation (among other things). They should also not be used for cryptographic applications; see cryptographically secure pseudo-random number generator for more suitable generators.
LCGs tend to exhibit some severe defects. For instance, if an LCG is used to choose points in an n-dimensional space, the points will lie on, at most, m1/n hyperplanes (Marsaglia's Theorem, developed by George Marsaglia). This is due to serial correlation between successive values of the sequence Xn. The spectral test, which is a simple test of an LCG's quality, is based on this fact.
A further problem of LCGs is that the lower-order bits of the generated sequence have a far shorter period than the sequence as a whole if m is set to a power of 2. In general, the nth least significant digit in the base b representation of the output sequence, where bk = m for some integer k, repeats with at most period bn.
Nevertheless, LCGs may be a good option. For instance, in an embedded system, the amount of memory available is often very severely limited. Similarly, in an environment such as a video game console taking a small number of high-order bits of an LCG may well suffice. The low-order bits of LCGs when m is a power of 2 should never be relied on for any degree of randomness whatsoever. Indeed, simply substituting 2^n for the modulus term reveals that the low order bits go through very short cycles. In particular, any full-cycle LCG when m is a power of 2 will produce alternately odd and even results!
[edit] Comparison with other PRNGs
If higher quality random numbers are needed, and sufficient memory is available (~ 2 kilobytes), then the Mersenne twister algorithm is a preferred choice. The Mersenne twister generates higher-quality deviates than almost any LCG. A common Mersenne twister implementation, interestingly enough, uses an LCG to generate seed data.
[edit] See also
[edit] Notes
- ^ "Linear Congruential Generators" by Joe Bolte, Wolfram Demonstrations Project.
- ^ Knuth 1997, pp. 17-19
- ^ Press, William H., et al. (1992)
[edit] References
- S.K. Park and K.W. Miller (1988). "Random Number Generators: Good Ones Are Hard To Find". Communications of the ACM 31 (10): 1192–1201. doi:. http://portal.acm.org/citation.cfm?id=63042.
- D. E. Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Section 3.2.1: The Linear Congruential Method, pp.10–26.
- P. L'Ecuyer (1999). "Tables of Linear Congruential Generators of Different Sizes and Good Lattice Structure". Mathematics of Computation 68 (225): 249–260. doi:. http://citeseer.ist.psu.edu/132363.html.
- Press, William H., et al. (1992). Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd edition. ISBN 0-521-43064-X.
- Joan Boyar (1989). "Inferring sequences produced by pseudo-random number generators". Journal of the ACM 36 (1): 129–141. doi:. http://portal.acm.org/citation.cfm?id=59305&dl=ACM&coll=portal. (in this paper, efficient algorithms are given for inferring sequences produced by certain pseudo-random number generators).
[edit] External links
- The simulation Linear Congruential Generator visualizes the correlations between the pseudo-random numbers when manipulating the parameters.
- Security of Random Number Generation: An Annotated Bibliography
- Linear Congruential Generators post to sci.math
