Depth-first search
From Wikipedia, the free encyclopedia
| Order in which the nodes are expanded | |
| Class | Search algorithm |
|---|---|
| Data structure | Graph |
| Worst case performance | O( | V | + | E | ) = O(bd) |
| Worst case space complexity | O(h) where h is the length of the longest simple path in the graph. |
| Optimal | no |
| Graph search algorithms |
|---|
| Search |
Depth-first search (DFS) is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root (selecting some node as the root in the graph case) and explores as far as possible along each branch before backtracking.
Contents |
[edit] Formal definition
Formally, DFS is an uninformed search that progresses by expanding the first child node of the search tree that appears and thus going deeper and deeper until a goal node is found, or until it hits a node that has no children. Then the search backtracks, returning to the most recent node it hasn't finished exploring. In a non-recursive implementation, all freshly expanded nodes are added to a stack for exploration.
Space complexity of DFS is much lower than BFS (breadth-first search). It also lends itself much better to heuristic methods of choosing a likely-looking branch. Time complexity of both algorithms are proportional to the number of vertices plus the number of edges in the graphs they traverse (O(|V| + |E|)).
When searching large graphs that cannot be fully contained in memory, DFS suffers from non-termination when the length of a path in the search tree is infinite. The simple solution of "remember which nodes I have already seen" doesn't always work because there can be insufficient memory. This can be solved by maintaining an increasing limit on the depth of the tree, which is called iterative deepening depth-first search.
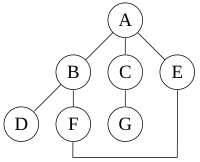
For the following graph:
a depth-first search starting at A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously-visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G.
Performing the same search without remembering previously visited nodes results in visiting nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.
Iterative deepening prevents this loop and will reach the following nodes on the following depths, assuming it proceeds left-to-right as above:
- 0: A
- 1: A (repeated), B, C, E
(Note that iterative deepening has now seen C, when a conventional depth-first search did not.)
- 2: A, B, D, F, C, G, E, F
(Note that it still sees C, but that it came later. Also note that it sees E via a different path, and loops back to F twice.)
- 3: A, B, D, F, E, C, G, E, F, B
For this graph, as more depth is added, the two cycles "ABFE" and "AEFB" will simply get longer before the algorithm gives up and tries another branch.
[edit] Output of a depth-first search
The most natural result of a depth first search of a graph (if it is considered as a function rather than a procedure) is a spanning tree of the vertices reached during the search. Based on this spanning tree, the edges of the original graph can be divided into three classes: forward edges, which point from a node of the tree to one of its descendants, back edges, which point from a node to one of its ancestors, and cross edges, which do neither. Sometimes tree edges, edges which belong to the spanning tree itself, are classified separately from forward edges. It can be shown that if the graph is undirected then all of its edges are tree edges or back edges.
[edit] Vertex orderings
It is also possible to use the depth-first search to linearly order the vertices (or nodes) of the original graph (or tree). There are three common ways of doing this:
- A preordering is a list of the vertices in the order that they were first visited by the depth-first search algorithm. This is a compact and natural way of describing the progress of the search, as was done earlier in this article. A preordering of an expression tree is the expression in Polish notation.
- A postordering is a list of the vertices in the order that they were last visited by the algorithm. A postordering of an expression tree is the expression in reverse Polish notation.
- A reverse postordering is the reverse of a postordering, i.e. a list of the vertices in the opposite order of their last visit. When searching a tree, reverse postordering is the same as preordering, but in general they are different when searching a graph. For example, when searching the directed graph
- beginning at node A, one visits the nodes in sequence, to produce lists either A B D B A C A, or A C D C A B A (depending upon the algorithm chooses to visit B or C first). Note that repeat visits in the form of backtracking to a node, to check if it has still unvisited neighbours, are included here (even if it is found to have none). Thus the possible preorderings are A B D C and A C D B (order by node's leftmost occurrence in above list), while the possible reverse postorderings are A C B D and A B C D (order by node's rightmost occurrence in above list). Reverse postordering produces a topological sorting of any directed acyclic graph. This ordering is also useful in control flow analysis as it often represents a natural linearization of the control flow. The graph above might represent the flow of control in a code fragment like
if (A) then {
B
} else {
C
}
D
- and it is natural to consider this code in the order A B C D or A C B D, but not natural to use the order A B D C or A C D B.
[edit] Pseudocode
A recursive version of the algorithm:
def dfs(v, visited = None, preorder_process = lambda x: None, postorder_process = lambda x: None): if visited is None: visited = set() visited.add(v) preorder_process(v) for neighbor in v.neighbors: if neighbor not in visited: dfs(neighbor, visited, preorder_process, postorder_process) postorder_process(v)
Another version, without the recursion:
def dfs(root, visited = None, preorder_process = lambda x: None): """ Given a starting vertex, root, do a depth-first search. """ import collections.deque to_visit = collections.deque() if visited is None: visited = set() to_visit.append(root) # Start with root while len(to_visit) != 0: v = to_visit.pop() if v not in visited: visited.add(v) preorder_process(v) to_visit.extend(v.neighbors)
[edit] Applications
Here are some algorithms where DFS is used:
- Finding connected components.
- Topological sorting.
- Finding 2-(edge or vertex)-connected components.
- Finding strongly connected components.
- Solving puzzles with only one solution, such as mazes.
[edit] References
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 22.3: Depth-first search, pp.540–549.
- Knuth, Donald E. (1997), The Art Of Computer Programming Vol 1. 3rd ed., Boston: Addison-Wesley, ISBN 0-201-89683-4, OCLC 155842391, http://www-cs-faculty.stanford.edu/~knuth/taocp.html