Splay tree

From Wikipedia, the free encyclopedia

Jump to: navigation, search

A splay tree is a self-balancing binary search tree with the additional property that recently accessed elements are quick to access again. It performs basic operations such as insertion, look-up and removal in O(log(n)) amortized time. For many non-uniform sequences of operations, splay trees perform better than other search trees, even when the specific pattern of the sequence is unknown. The splay tree was invented by Daniel Sleator and Robert Tarjan.

All normal operations on a binary search tree are combined with one basic operation, called splaying. Splaying the tree for a certain element rearranges the tree so that the element is placed at the root of the tree. One way to do this is to first perform a standard binary tree search for the element in question, and then use tree rotations in a specific fashion to bring the element to the top. Alternatively, a top-down algorithm can combine the search and the tree reorganization into a single phase.

Contents

[edit] Advantages and disadvantages

Good performance for a splay tree depends on the fact that it is self-balancing, and indeed self optimizing, in that frequently accessed nodes will move nearer to the root where they can be accessed more quickly. This is an advantage for nearly all practical applications, and is particularly useful for implementing caches and garbage collection algorithms; however it is important to note that for uniform access, a splay tree's performance will be considerably (although not asymptotically) worse than a somewhat balanced simple binary search tree.

Splay trees also have the advantage of being considerably simpler to implement than other self-balancing binary search trees, such as red-black trees or AVL trees, while their average-case performance is just as efficient. Also, splay trees do not need to store any bookkeeping data, thus minimizing memory requirements. However, these other data structures provide worst-case time guarantees, and can be more efficient in practice for uniform access.

One worst case issue with the basic splay tree algorithm is that of sequentially accessing all the elements of the tree in the sorted order. This leaves the tree completely unbalanced (this takes n accesses - each a O(log n) operation). Reaccessing the first item triggers an operation that takes O(n) operations to rebalance the tree before returning the first item. This is a significant delay for that final operation, although the amortized performance over the entire sequence is actually O(log n). However, recent research shows that randomly rebalancing the tree can avoid this unbalancing effect and give similar performance to the other self-balancing algorithms.[citation needed]

It is possible to create a persistent version of splay trees which allows access to both the previous and new versions after an update. This requires amortized O(log n) space per update.

Contrary to other types of self balancing trees, splay trees work well with nodes containing identical keys. Even with identical keys, performance remains amortized O(log n). All tree operations preserve the order of the identical nodes within the tree, which is a property similar to stable sorting algorithms. A carefully designed find operation can return the left most or right most node of a given key.

[edit] Operations

[edit] Splaying

When a node x is accessed, a splay operation is performed on x to move it to the root. To perform a splay operation we carry out a sequence of splay steps, each of which moves x closer to the root. By performing a splay operation on the node of interest after every access, the recently accessed nodes are kept near the root and the tree remains roughly balanced, so that we achieve the desired amortized time bounds.

Each particular step depends on three factors:

  • Whether x is the left or right child of its parent node, p,
  • whether p is the root or not, and if not
  • whether p is the left or right child of its parent, g (the grandparent of x).

The three types of splay steps are:

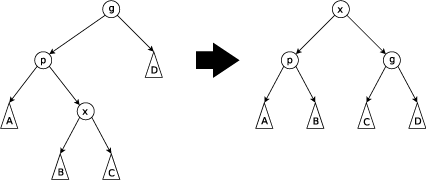
Zig Step: This step is done when p is the root. The tree is rotated on the edge between x and p. Zig steps exist to deal with the parity issue and will be done only as the last step in a splay operation and only when x has odd depth at the beginning of the operation.

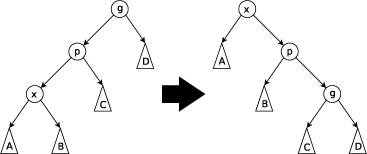
Zig-zig Step: This step is done when p is not the root and x and p are either both right children or are both left children. The picture below shows the case where x and p are both left children. The tree is rotated on the edge joining p with its parent g, then rotated on the edge joining x with p. Note that zig-zig steps are the only thing that differentiate splay trees from the rotate to root method introduced by Allen and Munro prior to the introduction of splay trees.

Zig-zag Step: This step is done when p is not the root and x is a right child and p is a left child or vice versa. The tree is rotated on the edge between x and p, then rotated on the edge between x and its new parent g.


[edit] Insertion

The process of inserting a node x into a splay tree is different to inserting a node into a binary tree. The reason is that after insertion we want x to be the new root of the splay tree.

First, we search x in the splay tree. If x does not already exist, then we will not find it, but its parent node y. Second, we perform a splay operation on y which will move y to the root of the splay tree. Third, we insert the node x as root in an appropriate way. In this way either y is left or right child of the new root x.

[edit] Deletion

The deletion operation for splay trees is somewhat different than for binary or AVL trees. To delete an arbitrary node x from a splay tree, the following steps can be followed:

1. Splay node x, sending it to the root of the tree.
2. Perform a left tree rotation on the first left child of x until the first left child of x has no right children.
3. Delete x from the tree & replace the root with the first left child of x.

[edit] Performance theorems

There are several theorems and conjectures regarding the worst-case runtime for performing a sequence S of m accesses in a splay tree containing n elements.

Balance Theorem[1]
The cost of performing the sequence S is O(m(logn + 1) + nlogn). In other words, splay trees perform as well as static balanced binary search trees on sequences of at least n accesses.
Static Optimality Theorem[1]
Let qi be the number of times element i is accessed in S. The cost of performing S is O\left (m+\sum_{i=1}^n q_i\log\frac{m}{q_i}\right). In other words, splay trees perform as well as optimum static binary search trees on sequences of at least n accesses.
Static Finger Theorem[1]
Let ij be the element accessed in the jth access of S and let f be any fixed element (the finger). The cost of performing S is O\Bigl(m+n\log n+\sum_{j=1}^m \log(|i_j-f|+1)\Bigr).
Working Set Theorem[1]
Let t(j) be the number of distinct elements accessed between access j and the previous time element ij was accessed. The cost of performing S is O\Bigl(m+n\log n+\sum_{j=1}^m \log(t(j)+1)\Bigr).
Dynamic Finger Theorem[2][3]
The cost of performing S is O\Bigl(m+n+\sum_{j=1}^m \log(|i_{j+1}-i_j|+1)\Bigr).
Scanning Theorem[4]
Also known as the Sequential Access Theorem. Accessing the n elements of a splay tree in symmetric order takes Θ(n) time, regardless of the initial structure of the splay tree. The tightest upper bound proven so far is 4.5n.[5]

[edit] Dynamic optimality conjecture

In addition to the proven performance guarantees for splay trees there is an unproven conjecture of great interest from the original Sleator and Tarjan paper. This conjecture is known as the dynamic optimality conjecture and it basically claims that splay trees perform as well as any other binary search tree algorithm up to a constant factor.

Dynamic Optimality Conjecture:[1] Let A be any binary search tree algorithm that accesses an element x by traversing the path from the root to x at a cost of d(x) + 1, and that between accesses can make any rotations in the tree at a cost of 1 per rotation. Let A(S) be the cost for A to perform the sequence S of accesses. Then the cost for a splay tree to perform the same accesses is O(n + A(S)).

There are several corollaries of the dynamic optimality conjecture that remain unproven:

Traversal Conjecture:[1] Let T1 and T2 be two splay trees containing the same elements. Let S be the sequence obtained by visiting the elements in T2 in preorder (i.e. depth first search order). The total cost of performing the sequence S of accesses on T1 is O(n).
Deque Conjecture:[6][7][4] Let S be a sequence of m double-ended queue operations (push, pop, inject, eject). Then the cost of performing S on a splay tree is O(m + n).
Split Conjecture:[8] Let S be any permutation of the elements of the splay tree. Then the cost of deleting the elements in the order S is O(n).

[edit] See also

[edit] References

  1. ^ a b c d e f Sleator, Daniel D.; Tarjan, Robert E. (1985), "Self-Adjusting Binary Search Trees", Journal of the ACM 32 (3): pp. 652-686, http://www.cs.cmu.edu/~sleator/papers/self-adjusting.pdf 
  2. ^ R. Cole, B. Mishra, J. Schmidt, A. Siegel. On the Dynamic Finger Conjecture for Splay Trees. Part I: Splay Sorting log n-Block Sequences. SIAM Journal on Computing 30, pages 1-43, 2000.
  3. ^ R. Cole. On the Dynamic Finger Conjecture for Splay Trees. Part II: The Proof. SIAM Journal on Computing 30, pages 44-85, 2000.
  4. ^ a b R.E. Tarjan. Sequential access in splay trees takes linear time. Combinatorica 5, pages 367-378, 1985.
  5. ^ Amr Elmasry. On the sequential access theorem and deque conjecture for splay trees. Theor. Comput. Sci. 314(3), pages 459-466, 2004.
  6. ^ S. Pettie. Splay Trees, Davenport-Schinzel Sequences, and the Deque Conjecture. In Proceedings 19th ACM-SIAM Symposium on Discrete Algorithms, pages 1115--1124, 2008.
  7. ^ R. Sundar. On the deque conjecture for the splay algorithm. Combinatorica 12(1):95--124, 1992.
  8. ^ J. Lucas. On the Competitiveness of Splay Trees: Relations to the Union-Find Problem. Online Algorithms, DIMACS Series in Discrete Mathematics and Theoretical Computer Science Vol. 7, pages 95--124, 1991.

[edit] External links

[edit] Algorithm

[edit] Implementations

[edit] Visualizations

Retrieved from "http://en.wikipedia.org/wiki/Splay_tree"
Personal tools