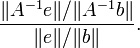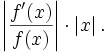Condition number

From Wikipedia, the free encyclopedia

In numerical analysis, the condition number associated with a problem is a measure of that problem's amenability to digital computation, that is, how numerically well-conditioned the problem is. A problem with a low condition number is said to be well-conditioned, while a problem with a high condition number is said to be ill-conditioned.

[edit] The condition number of a matrix

For example, the condition number associated with the linear equation $A x = b$ gives a bound on how inaccurate the solution $x$ will be after approximate solution. Note that this is before the effects of round-off error are taken into account; conditioning is a property of the matrix, not the algorithm or floating point accuracy of the computer used to solve the corresponding system. In particular, one should think of the condition number as being (very roughly) the rate at which the solution, $x$ , will change with respect to a change in $b$ . Thus, if the condition number is large, even a small error in $b$ may cause a large error in $x$ . On the other hand, if the condition number is small then the error in $x$ will not be much bigger than the error in $b$ .

The condition number is defined more precisely to be the maximum ratio of the relative error in $x$ divided by the relative error in $b$ .

Let $e$ be the error in $b$ . Then the error in the solution $A - 1 b$ is $A - 1 e$ . The ratio of the relative error in the solution to the relative error in $b$ is

$\frac{\Vert A^{-1} e\Vert / \Vert A^{-1} b\Vert}{\Vert e\Vert / \Vert b\Vert}.$

This is easily transformed to

$(\Vert A^{-1} e\Vert / \Vert e\Vert) \cdot (\Vert b\Vert / \Vert A^{-1} b\Vert).$

The maximum value (for nonzero $b$ and $e$ ) is easily seen to be the product of the two operator norms:

$\kappa (A) = \Vert A\Vert \cdot \Vert A^{-1}\Vert.$

The same definition is used for any consistent norm. This number arises so often in numerical linear algebra that it is given a name, the condition number of a matrix.

Of course, this definition depends on the choice of norm.

If $\|\cdot\|$ is $l 2$ norm then

$\kappa(A) = \frac{\sigma_\max(A)}{\sigma_\min(A)}$ where

σ max (A)

and

σ min (A)

are maximal and minimal singular values of

A

respectively. Hence

If $A$ is normal then

$\kappa(A) = \left|\frac{\lambda_\max(A)}{\lambda_\min(A)}\right|$ ( $\lambda_\max(A),\ \lambda_\min(A)$ are maximal and minimal (by moduli) eigenvalues of

A

respectively)

If $A$ is unitary then

$\kappa(A) = 1. \,$

If $\|\cdot\|$ is $l_{\infty}$ norm and $A$ is lower triangular non-singular (i.e., $a_{ii} \ne 0 \; \forall i$ ) then

$\kappa(A) \geq \frac{\max_i(|a_{ii}|)}{\min_i(|a_{ii}|)}.$

[edit] The condition number in other contexts

Condition numbers for singular-value decompositions, polynomial root finding, eigenvalue and many other problems may be defined.

Generally, if a numerical problem is well-posed, it can be expressed as a function $f$ mapping its data, which is an $m$ -tuple of real numbers $x$ , into its solution, an $n$ -tuple of real numbers $f (x)$ .

Its condition number is then defined to be the maximum value of the ratio of the relative errors in the solution to the relative error in the data, over the problem domain:

$\max \left\{ \left| \frac{f(x) - f(x^*)}{f(x)} \right| \left/ \left| \frac{x - x^*}{x} \right| \right. : |x - x^*| < \epsilon \right\}$