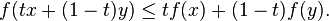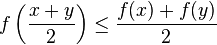Convex function

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In mathematics, a real-valued function f defined on an interval (or on any convex subset of some vector space) is called convex, concave upwards, concave up or convex cup, if for any two points x and y in its domain C and any t in [0,1], we have

f(tx+(1-t)y)\leq t f(x)+(1-t)f(y).
Convex function on an interval.

In other words, a function is convex if and only if its epigraph (the set of points lying on or above the graph) is a convex set.

Pictorially, a function is called 'convex' if the function lies below the straight line segment connecting two points, for any two points in the interval.[1]

A function is called strictly convex if

f(tx+(1-t)y) < t f(x)+(1-t)f(y)\,

for any t in (0,1) and x \neq y.

A function f is said to be concave if − f is convex.

Contents

[edit] Properties

A function (in blue) is convex if and only if the region above its graph (in green) is a convex set.

A convex function f defined on some open interval C is continuous on C and differentiable at all but at most countably many points. If C is closed, then f may fail to be continuous at the endpoints of C.

A function is midpoint convex on an interval C if

f\left( \frac{x+y}{2} \right) \le \frac{f(x)+f(y)}{2}

for all x and y in C. This condition is only slightly weaker than convexity. For example, a real valued Lebesgue measurable function that is midpoint convex will be convex [2]. In particular, a continuous function that is midpoint convex will be convex.

A differentiable function of one variable is convex on an interval if and only if its derivative is monotonically non-decreasing on that interval.

A continuously differentiable function of one variable is convex on an interval if and only if the function lies above all of its tangents: f(y) ≥ f(x) + f '(x) (y − x) for all x and y in the interval. In particular, if f '(c) = 0, then c is a global minimum of f(x).

A twice differentiable function of one variable is convex on an interval if and only if its second derivative is non-negative there; this gives a practical test for convexity. If its second derivative is positive then it is strictly convex, but the converse does not hold. For example, the second derivative of f(x) = x4 is f "(x) = 12 x2, which is zero for x = 0, but x4 is strictly convex.

More generally, a continuous, twice differentiable function of several variables is convex on a convex set if and only if its Hessian matrix is positive semidefinite on the interior of the convex set.

Any local minimum of a convex function is also a global minimum. A strictly convex function will have at most one global minimum.

For a convex function f, the sublevel sets {x | f(x) < a} and {x | f(x) ≤ a} with a ∈ R are convex sets. However, a function whose sublevel sets are convex sets may fail to be a convex function; such a function is called a quasiconvex function.

Jensen's inequality applies to every convex function f. If X is a random variable taking values in the domain of f, then 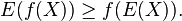E(f(X)) \geq f(E(X)). (Here E denotes the mathematical expectation.)

[edit] Convex function calculus

  • If f and g are convex functions, then so are m(x) = max{f(x),g(x)} and h(x) = f(x) + g(x).
  • If f and g are convex functions and if g is increasing, then h(x) = g(f(x)) is convex.
  • Convexity is invariant under affine maps: that is, if f(x) is convex with 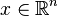x\in\mathbb{R}^n, then so is g(y) = f(Ay + b), where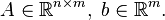 A\in\mathbb{R}^{n \times m},\; b\in\mathbb{R}^m.
  • If f(x,y) is convex in (x,y) and C is a convex nonempty set, then g(x) = \inf_{y\in C} f(x,y) is convex in x, provided g(x) > -\infty for some x.

[edit] Examples

  • The function f(x) = x2 has f\,''(x)=2>0 at all points, so f is a (strictly) convex function.
  • The absolute value function f(x) = | x | is convex, even though it does not have a derivative at the point x = 0.
  • The function f(x) = | x | p for 1 ≤ p is convex.
  • The exponential function f(x) = ex is convex. More generally, the function g(x) = ef(x) is logarithmically convex if f is a convex function.
  • The function f with domain [0,1] defined by f(0)=f(1)=1, f(x)=0 for 0<x<1 is convex; it is continuous on the open interval (0,1), but not continuous at 0 and 1.
  • The function x3 has second derivative 6x; thus it is convex on the set where x ≥ 0 and concave on the set where x ≤ 0.
  • Every linear transformation taking values in \mathbb{R} is convex but not strictly convex, since if f is linear, then f(a + b) = f(a) + f(b). This statement also holds if we replace "convex" by "concave".
  • Every affine function taking values in \mathbb{R}, i.e., each function of the form f(x) = aTx + b, is simultaneously convex and concave.
  • Every norm is a convex function, by the triangle inequality.
  • If f is convex, the perspective function g(x,t) = tf(x / t) is convex for t > 0.
  • Examples of functions that are monotonically increasing but not convex include 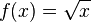f(x) = \sqrt x and g(x) = log(x).
  • Examples of functions that are convex but not monotonically increasing include h(x) = x2 and k(x) = − x.
  • The function f(x) = 1/x2, with f(0)=+∞, is convex on the interval (0,+∞) and convex on the interval (-∞,0), but not convex on the interval (-∞,+∞), because of the singularity at x = 0.

[edit] See also

[edit] References

  1. ^ 1
  2. ^ Sierpinski Theorem, Donoghue (1969), p. 12
  • Moon, Todd. "Tutorial: Convexity and Jensen's inequality". http://www.neng.usu.edu/classes/ece/7680/lecture2/node5.html. Retrieved on 2008-09-04. 
  • Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press. 
  • Luenberger, David (1984). Linear and Nonlinear Programming. Addison-Wesley. 
  • Luenberger, David (1969). Optimization by Vector Space Methods. Wiley & Sons. 
  • Bertsekas, Dimitri (2003). Convex Analysis and Optimization. Athena Scientific. 
  • Thomson, Brian (1994). Symmetric Properties of Real Functions. CRC Press. 
  • Donoghue, William F. (1969). Distributions and Fourier Transforms. Academic Press. 
  • Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
  • Krasnosel'skii M.A., Rutickii Ya.B. (1961). Convex Functions and Orlicz Spaces. Groningen: P.Noordhoff Ltd. 
  • Borwein, Jonathan, and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Convex_function"
Personal tools