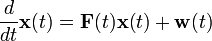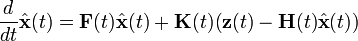Kalman filter
From Wikipedia, the free encyclopedia
The Kalman filter is an efficient recursive filter that estimates the state of a linear dynamic system from a series of noisy measurements. It is used in a wide range of engineering applications from radar to computer vision, and is an important topic in control theory and control systems engineering. Together with the linear-quadratic regulator (LQR), the Kalman filter solves the linear-quadratic-Gaussian control problem (LQG). The Kalman filter, the linear-quadratic regulator and the linear-quadratic-Gaussian controller are solutions to what probably are the most fundamental problems in control theory.
[edit] Example applications
An example application would be providing accurate, continuously updated information about the position and velocity of an object given only a sequence of observations about its position, each of which includes some error.
For a similar, more concrete example, in a radar application, where one is interested in tracking a target, information about the location, speed, and acceleration of the target is measured at each time instant, with a great deal of corruption by noise. The Kalman filter exploits the dynamics of the target, which govern its time evolution, to remove the effects of the noise and get a good estimate of the location of the target at the present time (filtering), at a future time (prediction), or at a time in the past (interpolation or smoothing).
[edit] Naming and historical development
The filter is named after Rudolf E. Kalman, though Thorvald Nicolai Thiele[1] and Peter Swerling developed a similar algorithm earlier. Stanley F. Schmidt is generally credited with developing the first implementation of a Kalman filter. It was during a visit of Kalman to the NASA Ames Research Center that he saw the applicability of his ideas to the problem of trajectory estimation for the Apollo program, leading to its incorporation in the Apollo navigation computer. The filter was developed in papers by Swerling (1958), Kalman (1960), and Kalman and Bucy (1961).
The filter is sometimes called Stratonovich-Kalman-Bucy filter because it is a special case of a more general, non-linear filter developed earlier by Ruslan L. Stratonovich.[2][3] In fact, equations of the special case, linear filter appeared in these papers by Stratonovich that were published before summer 1960, when Kalman met with Stratonovich during a conference in Moscow.
In control theory, the Kalman filter is most commonly referred to as linear quadratic estimation (LQE).
A wide variety of Kalman filters have now been developed, from Kalman's original formulation, now called the simple Kalman filter, to Schmidt's extended filter, the information filter and a variety of square-root filters developed by Bierman, Thornton and many others. Perhaps the most commonly used type of Kalman filter is the phase-locked loop now ubiquitous in radios, computers, and nearly any other type of video or communications equipment.
[edit] Underlying dynamic system model
Kalman filters are based on linear dynamical systems discretised in the time domain. They are modelled on a Markov chain built on linear operators perturbed by Gaussian noise. The state of the system is represented as a vector of real numbers. At each discrete time increment, a linear operator is applied to the state to generate the new state, with some noise mixed in, and optionally some information from the controls on the system if they are known. Then, another linear operator mixed with more noise generates the visible outputs from the hidden state. The Kalman filter may be regarded as analogous to the hidden Markov model, with the key difference that the hidden state variables take values in a continuous space (as opposed to a discrete state space as in the hidden Markov model). Additionally, the hidden Markov model can represent an arbitrary distribution for the next value of the state variables, in contrast to the Gaussian noise model that is used for the Kalman filter. There is a strong duality between the equations of the Kalman Filter and those of the hidden Markov model. A review of this and other models is given in Roweis and Ghahramani (1999).[4]
In order to use the Kalman filter to estimate the internal state of a process given only a sequence of noisy observations, one must model the process in accordance with the framework of the Kalman filter. This means specifying the matrices Fk, Hk, Qk, Rk, and sometimes Bk for each time-step k as described below.

The Kalman filter model assumes the true state at time k is evolved from the state at (k − 1) according to
where
- Fk is the state transition model which is applied to the previous state xk−1;
- Bk is the control-input model which is applied to the control vector uk;
- wk is the process noise which is assumed to be drawn from a zero mean multivariate normal distribution with covariance Qk.
At time k an observation (or measurement) zk of the true state xk is made according to
where Hk is the observation model which maps the true state space into the observed space and vk is the observation noise which is assumed to be zero mean Gaussian white noise with covariance Rk.
The initial state, and the noise vectors at each step {x0, w1, ..., wk, v1 ... vk} are all assumed to be mutually independent.
Many real dynamical systems do not exactly fit this model; however, because the Kalman filter is designed to operate in the presence of noise, an approximate fit is often good enough for the filter to be very useful. Variations on the Kalman filter described below allow richer and more sophisticated models.
[edit] The Kalman filter
The Kalman filter is a recursive estimator. This means that only the estimated state from the previous time step and the current measurement are needed to compute the estimate for the current state. In contrast to batch estimation techniques, no history of observations and/or estimates is required. It is unusual in being purely a time domain filter; most filters (for example, a low-pass filter) are formulated in the frequency domain and then transformed back to the time domain for implementation. In what follows, the notation  represents the estimate of
represents the estimate of  at time n given observations up to, and including time m.
at time n given observations up to, and including time m.
The state of the filter is represented by two variables:
 , the estimate of the state at time k given observations up to and including time k;
, the estimate of the state at time k given observations up to and including time k;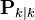 , the error covariance matrix (a measure of the estimated accuracy of the state estimate).
, the error covariance matrix (a measure of the estimated accuracy of the state estimate).
The Kalman filter has two distinct phases: Predict and Update. The predict phase uses the state estimate from the previous timestep to produce an estimate of the state at the current timestep. In the update phase, measurement information at the current timestep is used to refine this prediction to arrive at a new, (hopefully) more accurate state estimate, again for the current timestep.
[edit] Predict
| Predicted state |
|
|
Predicted estimate covariance |
|
[edit] Update
| Innovation or measurement residual |
|
| Innovation (or residual) covariance |  |
| Optimal Kalman gain |  |
| Updated state estimate |  |
| Updated estimate covariance |  |
The formula for the updated estimate covariance above is only valid for the optimal Kalman gain. Usage of other gain values require a more complex formula found in the derivations section.
[edit] Invariants
If the model is accurate, and the values for  and
and  accurately reflect the distribution of the initial state values, then the following invariants are preserved: all estimates have mean error zero
accurately reflect the distribution of the initial state values, then the following invariants are preserved: all estimates have mean error zero
where E[ξ] is the expected value of ξ, and covariance matrices accurately reflect the covariance of estimates
[edit] Examples
Consider a truck on perfectly frictionless, infinitely long straight rails. Initially the truck is stationary at position 0, but it is buffeted this way and that by random acceleration. We measure the position of the truck every Δt seconds, but these measurements are imprecise; we want to maintain a model of where the truck is and what its velocity is. We show here how we derive the model from which we create our Kalman filter.
There are no controls on the truck, so we ignore Bk and uk. Since F, H, R and Q are constant, their time indices are dropped.
The position and velocity of the truck is described by the linear state space
where  is the velocity, that is, the derivative of position with respect to time.
is the velocity, that is, the derivative of position with respect to time.
We assume that between the (k − 1)th and kth timestep the truck undergoes a constant acceleration of ak that is normally distributed, with mean 0 and standard deviation σa. From Newton's laws of motion we conclude that
where
and
We find that
![\textbf{Q} = \textrm{cov}(\textbf{G}a) = \textrm{E}[(\textbf{G}a)(\textbf{G}a)^{\text{T}}] = \textbf{G} \textrm{E}[a^2] \textbf{G}^{\text{T}} = \textbf{G}[\sigma_a^2]\textbf{G}^{\text{T}} = \sigma_a^2 \textbf{G}\textbf{G}^{\text{T}}](http://upload.wikimedia.org/math/a/3/5/a35c82aabf9ae1297ef04300537c8112.png) (since σa is a scalar).
(since σa is a scalar).
At each time step, a noisy measurement of the true position of the truck is made. Let us suppose the noise is also normally distributed, with mean 0 and standard deviation σz.
where
and
We know the initial starting state of the truck with perfect precision, so we initialize
and to tell the filter that we know the exact position, we give it a zero covariance matrix:
If the initial position and velocity are not known perfectly the covariance matrix should be initialized with a suitably large number, say B, on its diagonal.
The filter will then prefer the information from the first measurements over the information already in the model.
[edit] Derivations
[edit] Deriving the posterior estimate covariance matrix
Starting with our invariant on the error covariance Pk|k as above
substitute in the definition of 
and substitute 
and 
and by collecting the error vectors we get
Since the measurement error vk is uncorrelated with the other terms, this becomes
by the properties of vector covariance this becomes
which, using our invariant on Pk|k-1 and the definition of Rk becomes
This formula (sometimes known as the "Joseph form" of the covariance update equation) is valid no matter what the value of Kk. It turns out that if Kk is the optimal Kalman gain, this can be simplified further as shown below.
[edit] Kalman gain derivation
The Kalman filter is a minimum mean-square error estimator. The error in the posterior state estimation is
We seek to minimize the expected value of the square of the magnitude of this vector, ![\textrm{E}[|\textbf{x}_{k} - \hat{\textbf{x}}_{k|k}|^2]](http://upload.wikimedia.org/math/d/a/c/dac65520055c06e789c58462cc7b7738.png) . This is equivalent to minimizing the trace of the posterior estimate covariance matrix
. This is equivalent to minimizing the trace of the posterior estimate covariance matrix 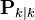 . By expanding out the terms in the equation above and collecting, we get:
. By expanding out the terms in the equation above and collecting, we get:
The trace is minimized when the matrix derivative is zero:
Solving this for Kk yields the Kalman gain:
This gain, which is known as the optimal Kalman gain, is the one that yields MMSE estimates when used.
[edit] Simplification of the posterior error covariance formula
The formula used to calculate the posterior error covariance can be simplified when the Kalman gain equals the optimal value derived above. Multiplying both sides of our Kalman gain formula on the right by SkKkT, it follows that
Referring back to our expanded formula for the posterior error covariance,
we find the last two terms cancel out, giving
This formula is computationally cheaper and thus nearly always used in practice, but is only correct for the optimal gain. If arithmetic precision is unusually low causing problems with numerical stability, or if a non-optimal Kalman gain is deliberately used, this simplification cannot be applied; the posterior error covariance formula as derived above must be used.
[edit] Relationship to the digital filter
The Kalman filter can be regarded as an adaptive low-pass infinite impulse response digital filter, with cut-off frequency depending on the ratio between the process- and measurement (or observation) noise, as well as the estimate covariance. Frequency response is, however, rarely of interest when designing state estimators such as the Kalman Filter, whereas for digital filters such as IIR and FIR filters, frequency response is usually of primary concern. For the Kalman Filter, the important goal is how accurate the filter is, and this is most often decided based on empirical Monte Carlo simulations, where "truth" (the true state) is known.
[edit] Relationship to recursive Bayesian estimation
The true state is assumed to be an unobserved Markov process, and the measurements are the observed states of a hidden Markov model.
Because of the Markov assumption, the true state is conditionally independent of all earlier states given the immediately previous state.
Similarly the measurement at the k-th timestep is dependent only upon the current state and is conditionally independent of all other states given the current state.
Using these assumptions the probability distribution over all states of the hidden Markov model can be written simply as:
However, when the Kalman filter is used to estimate the state x, the probability distribution of interest is that associated with the current states conditioned on the measurements up to the current timestep. (This is achieved by marginalizing out the previous states and dividing by the probability of the measurement set.)
This leads to the predict and update steps of the Kalman filter written probabilistically. The probability distribution associated with the predicted state is the sum (integral) of the products of the probability distribution associated with the transition from the (k - 1)-th timestep to the k-th and the probability distribution associated with the previous state, over all possible 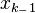 .
.
The measurement set up to time t is
The probability distribution of the update is proportional to the product of the measurement likelihood and the predicted state.
The denominator
is a normalization term.
The remaining probability density functions are
Note that the PDF at the previous timestep is inductively assumed to be the estimated state and covariance. This is justified because, as an optimal estimator, the Kalman filter makes best use of the measurements, therefore the PDF for  given the measurements
given the measurements  is the Kalman filter estimate.
is the Kalman filter estimate.
[edit] Information filter
In the information filter, or inverse covariance filter, the estimated covariance and estimated state are replaced by the information matrix and information vector respectively. These are defined as:
Similarly the predicted covariance and state have equivalent information forms, defined as:
as have the measurement covariance and measurement vector, which are defined as:
The information update now becomes a trivial sum.
The main advantage of the information filter is that N measurements can be filtered at each timestep simply by summing their information matrices and vectors.
To predict the information filter the information matrix and vector can be converted back to their state space equivalents, or alternatively the information space prediction can be used.
Note that if F and Q are time invariant these values can be cached. Note also that F and Q need to be invertible.
[edit] Fixed-lag smoother
The optimal fixed-lag smoother provides the optimal estimate of  for a given fixed-lag N using the measurements from
for a given fixed-lag N using the measurements from  to
to  . It can be derived using the previous theory via an augmented state, and the main equation of the filter is the following:
. It can be derived using the previous theory via an augmented state, and the main equation of the filter is the following:

where:
1) 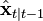 is estimated via a standard Kalman filter;
is estimated via a standard Kalman filter;
2) 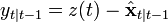 is the innovation produced considering the estimate of the standard Kalman filter;
is the innovation produced considering the estimate of the standard Kalman filter;
3) the various 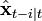 with
with  are new variables, i.e. they do not appear in the standard Kalman filter;
are new variables, i.e. they do not appear in the standard Kalman filter;
4) the gains are computed via the following scheme:
![K^{(i)} =
P^{(i)} H^{T}
\left[
H P H^{T} + R
\right]^{-1}](http://upload.wikimedia.org/math/8/4/c/84c9732d7cc69960772a191e4d09eaed.png)
and
![P^{(i)} =
P
\left[
\left[
F - K H
\right]^{T}
\right]^{i}](http://upload.wikimedia.org/math/2/4/d/24d65d3a8c4f87b6d2902be6ae846da9.png)
where P and K are the prediction error covariance and the gains of the standard Kalman filter.
Note that if we define the estimation error covariance
![P_{i} :=
E
\left[
\left(
\textbf{x}_{t-i} - \hat{\textbf{x}}_{t-i|t}
\right)^{*}
\left(
\textbf{x}_{t-i} - \hat{\textbf{x}}_{t-i|t}
\right)
|
z_{1} \ldots z_{t}
\right]](http://upload.wikimedia.org/math/d/a/8/da87142b1755f022e7615ea5bce2770a.png)
then we have that the improvement on the estimation of  is given by:
is given by:
![P - P_{i} =
\sum_{j = 0}^{i}
\left[
P^{(j)} H^{T}
\left[
H P H^{T} + R
\right]^{-1}
H \left( P^{(i)} \right)^{T}
\right]](http://upload.wikimedia.org/math/1/6/0/1607f4f21976ef2cac996926f36aad95.png)
[edit] Non-linear filters
The basic Kalman filter is limited to a linear assumption. However, most non-trivial systems are non-linear. The non-linearity can be associated either with the process model or with the observation model or with both.
[edit] Extended Kalman filter
In the extended Kalman filter, (EKF) the state transition and observation models need not be linear functions of the state but may instead be (differentiable) functions.
The function f can be used to compute the predicted state from the previous estimate and similarly the function h can be used to compute the predicted measurement from the predicted state. However, f and h cannot be applied to the covariance directly. Instead a matrix of partial derivatives (the Jacobian) is computed.
At each timestep the Jacobian is evaluated with current predicted states. These matrices can be used in the Kalman filter equations. This process essentially linearizes the non-linear function around the current estimate.
[edit] Unscented Kalman filter
When the state transition and observation models – that is, the predict and update functions f and h (see above) – are highly non-linear, the extended Kalman filter can give particularly poor performance [JU97]. This is because only the mean is propagated through the non-linearity. The unscented Kalman filter (UKF) [JU97] uses a deterministic sampling technique known as the unscented transform to pick a minimal set of sample points (called sigma points) around the mean. These sigma points are then propagated through the non-linear functions, and the covariance of the estimate is then recovered. The result is a filter which more accurately captures the true mean and covariance. (This can be verified using Monte Carlo sampling or through a Taylor series expansion of the posterior statistics.) In addition, this technique removes the requirement to explicitly calculate Jacobians, which for complex functions can be a difficult task in itself (i.e., requiring complicated derivatives if done analytically or being computationally costly if done numerically).
Predict
As with the EKF, the UKF prediction can be used independently from the UKF update, in combination with a linear (or indeed EKF) update, or vice versa.
The estimated state and covariance are augmented with the mean and covariance of the process noise.
A set of 2L+1 sigma points is derived from the augmented state and covariance where L is the dimension of the augmented state.
where
is the ith column of the matrix square root of
using the definition: square root A of matrix B satisfies
-
 .
.
The matrix square root should be calculated using numerically efficient and stable methods such as the Cholesky decomposition.
The sigma points are propagated through the transition function f.
The weighted sigma points are recombined to produce the predicted state and covariance.
where the weights for the state and covariance are given by:
Typical values for α, β, and κ are 10 − 3, 2 and 0 respectively. (These values should suffice for most purposes.)
Update
The predicted state and covariance are augmented as before, except now with the mean and covariance of the measurement noise.
As before, a set of 2L + 1 sigma points is derived from the augmented state and covariance where L is the dimension of the augmented state.
Alternatively if the UKF prediction has been used the sigma points themselves can be augmented along the following lines
where
The sigma points are projected through the observation function h.
The weighted sigma points are recombined to produce the predicted measurement and predicted measurement covariance.
The state-measurement cross-covariance matrix,
is used to compute the UKF Kalman gain.
As with the Kalman filter, the updated state is the predicted state plus the innovation weighted by the Kalman gain,
And the updated covariance is the predicted covariance, minus the predicted measurement covariance, weighted by the Kalman gain.
[edit] Kalman-Bucy filter
The Kalman-Bucy filter is a continuous time version of the Kalman filter.[5][6]
It is based on the state space model
where the covariances of the noise terms 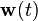 and
and 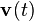 are given by
are given by  and
and  , respectively.
, respectively.
The filter consists of two differential equations, one for the state estimate and one for the covariance:
where the Kalman gain is given by
Note that in this expression for  the covariance of the observation noise
the covariance of the observation noise  represents at the same time the covariance of the prediction error (or innovation)
represents at the same time the covariance of the prediction error (or innovation)  ; these covariances are equal only in the case of continuous time.[7]
; these covariances are equal only in the case of continuous time.[7]
The distinction between the prediction and update steps of discrete-time Kalman filtering does not exist in continuous time.
The second differential equation, for the covariance, is an example of a Riccati equation.
[edit] Applications
- Batteries State of Charge(SoC) Estimation [1][2]
- Autopilot
- Brain-computer interface
- Dynamic positioning
- Economics, in particular macroeconomics, time series, and econometrics
- Inertial guidance system
- Radar tracker
- Satellite navigation systems
- Simultaneous localization and mapping
- Chaotic signals
- Weather forecasting
- Speech enhancement
[edit] See also
- Ensemble Kalman filter
- Fast Kalman filter
- Compare with: Wiener filter, and the multimodal Particle filter estimator.
- Non-linear filter
- Predictor corrector
- Separation principle
- Zakai equation
- Recursive least squares
- Data assimilation
- Stochastic differential equations
- Filtering problem (stochastic processes)
- Volterra series
[edit] References
- ^ Steffen L. Lauritzen, Thiele: Pioneer in Statistics, Oxford University Press, 2002. ISBN 0-19-850972-3.
- ^ Stratonovich, R.L. (1959). Optimum nonlinear systems which bring about a separation of a signal with constant parameters from noise. Radiofizika, 2:6, pp. 892-901.
- ^ Stratonovich, R.L. (1960) Application of the Markov processes theory to optimal filtering. Radio Engineering and Electronic Physics, 5:11, pp.1-19.
- ^ Roweis, S. and Ghahramani, Z., A unifying review of linear Gaussian models, Neural Comput. Vol. 11, No. 2, (February 1999), pp. 305-345.
- ^ Bucy, R.S. and Joseph, P.D., Filtering for Stochastic Processes with Applications to Guidance, John Wiley & Sons, 1968; 2nd Edition, AMS Chelsea Publ., 2005. ISBN 0821837826
- ^ Jazwinski, Andrew H., Stochastic processes and filtering theory, Academic Press, New York, 1970. ISBN 0123815509
- ^ Kailath, Thomas, "An innovation approach to least-squares estimation Part I: Linear filtering in additive white noise", IEEE Transactions on Automatic Control, 13(6), 646-655, 1968
[edit] Further reading
- Gelb, A. (1974). Applied Optimal Estimation. MIT Press.
- Kalman, R.E. (1960). "A new approach to linear filtering and prediction problems". Journal of Basic Engineering 82 (1): 35–45. http://www.elo.utfsm.cl/~ipd481/Papers%20varios/kalman1960.pdf. Retrieved on 2008-05-03.
- Kalman, R.E.; Bucy, R.S. (1961). New Results in Linear Filtering and Prediction Theory.. http://stinet.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=ADD518892. Retrieved on 2008-05-03.
- Julier, S.J.; Uhlmann, J.K. (1997). "A new extension of the Kalman filter to nonlinear systems". Int. Symp. Aerospace/Defense Sensing, Simul. and Controls 3. http://www.cs.unc.edu/~welch/kalman/media/pdf/Julier1997_SPIE_KF.pdf. Retrieved on 2008-05-03.
- Harvey, A.C. (1990). Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press.
- Roweis, S.; Ghahramani, Z. (1999). "A Unifying Review of Linear Gaussian Models". Neural Computation 11 (2): 305–345. doi:.
- Simon, D. (2006). Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. Wiley-Interscience. http://academic.csuohio.edu/simond/estimation/.
- Stengel, R.F. (1994). Optimal Control and Estimation. Courier Dover Publications.
- Warwick, K. (1987). "Optimal observers for ARMA models". International Journal of Control 46 (5): 1493–1503. doi:. http://www.informaworld.com/index/779885789.pdf. Retrieved on 2008-05-03.
- Bierman, G.J. (1977). "Factorization Methods for Discrete Sequential Estimation". Mathematics in Science and Engineering 128.
- Bozic, S.M. (1994). Digital and Kalman filtering. Butterworth-Heinemann.
[edit] External links
- A New Approach to Linear Filtering and Prediction Problems, by R. E. Kalman, 1960
- Kalman-Bucy Filter, a good derivation of the Kalman-Bucy Filter
- An Introduction to the Kalman Filter, SIGGRAPH 2001 Course, Greg Welch and Gary Bishop
- Kalman filtering chapter from Stochastic Models, Estimation, and Control, vol. 1, by Peter S. Maybeck
- Kalman Filter webpage, with lots of links
- Kalman Filtering
- Kalman Filters, thorough introduction to several types, together with applications to Robot Localization
- Kalman filters used in Weather models, SIAM News, Volume 36, Number 8, October 2003.
- Critical Evaluation of Extended Kalman Filtering and Moving-Horizon Estimation, Ind. Eng. Chem. Res., 44 (8), 2451 -2460, 2005.
- Source code for the propeller microprocessor: Well documented source code written for the Parallax propeller processor.
- Gerald J. Bierman's Estimation Subroutine Library: Corresponds to the code in the research monograph "Factorization Methods for Discrete Sequential Estimation" originally published by Academic Press in 1977. Republished by Dover
- Matlab Toolbox of Kalman Filtering applied to Simultaneous Localization and Mapping: Vehicle moving in 1D, 2D and 3D
- Derivation of a 6D EKF solution to Simultaneous Localization and Mapping (In PDF). See also the tutorial on implementing a Kalman Filter with the MRPT C++ libraries.
- Beyond Kalman Filters: State estimation with nonlinear models
- Kalman filter Detailed mathematical derivations.


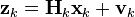

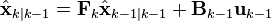
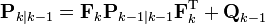

![\textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0](http://upload.wikimedia.org/math/4/c/4/4c4bbb2da083dae032f5a7930e7b5d80.png)
![\textrm{E}[\tilde{\textbf{y}}_k] = 0](http://upload.wikimedia.org/math/0/0/7/00703cccab98e464367ae2b34e9b1493.png)

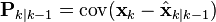
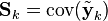

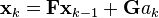


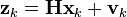

![\textbf{R} = \textrm{E}[\textbf{v}_k \textbf{v}_k^{\text{T}}] = \begin{bmatrix} \sigma_z^2 \end{bmatrix}](http://upload.wikimedia.org/math/1/3/c/13c0f6c1c05e1576664884f7b32ba0e2.png)

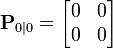
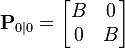
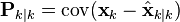



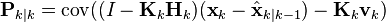
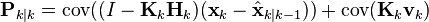








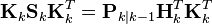
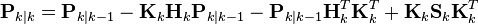


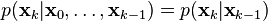

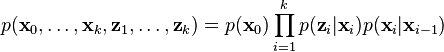

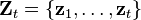



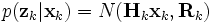

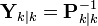



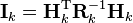





![\textbf{M}_{k} =
[\textbf{F}_{k}^{-1}]^{\text{T}} \textbf{Y}_{k-1|k-1} \textbf{F}_{k}^{-1}](http://upload.wikimedia.org/math/2/6/2/26208bc8cd8a6061d4e26c0165797af5.png)
![\textbf{C}_{k} =
\textbf{M}_{k} [\textbf{M}_{k}+\textbf{Q}_{k}^{-1}]^{-1}](http://upload.wikimedia.org/math/b/a/b/baba972b698cfcfce00c6fdb6c3c52e9.png)
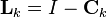
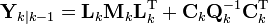
![\hat{\textbf{y}}_{k|k-1} =
\textbf{L}_{k} [\textbf{F}_{k}^{-1}]^{\text{T}}\hat{\textbf{y}}_{k-1|k-1}](http://upload.wikimedia.org/math/a/d/a/adaa6e7d41ff680f915be3e0d4d2e4ca.png)

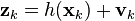
![\textbf{x}_{k-1|k-1}^{a} = [ \hat{\textbf{x}}_{k-1|k-1}^{T} \quad E[\textbf{w}_{k}^{T}] \ ]^{T}](http://upload.wikimedia.org/math/7/c/0/7c0c53eef72ef92fff5265ffd5a5f68d.png)
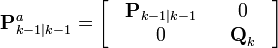







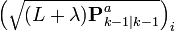


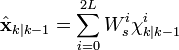
![\textbf{P}_{k|k-1} = \sum_{i=0}^{2L} W_{c}^{i}\ [\chi_{k|k-1}^{i} - \hat{\textbf{x}}_{k|k-1}] [\chi_{k|k-1}^{i} - \hat{\textbf{x}}_{k|k-1}]^{T}](http://upload.wikimedia.org/math/5/1/a/51a88054b452591833406b0018a83781.png)



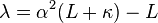
![\textbf{x}_{k|k-1}^{a} = [ \hat{\textbf{x}}_{k|k-1}^{T} \quad E[\textbf{v}_{k}^{T}] \ ]^{T}](http://upload.wikimedia.org/math/f/a/6/fa6d80e1bb88f3fe9739339130520c8d.png)
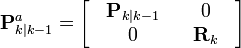




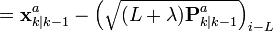
![\chi_{k|k-1} := [ \chi_{k|k-1}^T \quad E[\textbf{v}_{k}^{T}] \ ]^{T} \pm \sqrt{ (L + \lambda) \textbf{R}_{k}^{a} }](http://upload.wikimedia.org/math/9/6/9/9696ba46d924b5cca5cc17de316051a4.png)

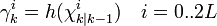

![\textbf{P}_{z_{k}z_{k}} = \sum_{i=0}^{2L} W_{c}^{i}\ [\gamma_{k}^{i} - \hat{\textbf{z}}_{k}] [\gamma_{k}^{i} - \hat{\textbf{z}}_{k}]^{T}](http://upload.wikimedia.org/math/e/9/0/e90ffca95f76247b8363aae1001dd8c2.png)
![\textbf{P}_{x_{k}z_{k}} = \sum_{i=0}^{2L} W_{c}^{i}\ [\chi_{k|k-1}^{i} - \hat{\textbf{x}}_{k|k-1}] [\gamma_{k}^{i} - \hat{\textbf{z}}_{k}]^{T}](http://upload.wikimedia.org/math/2/c/9/2c9c83f91f94b10ce37f1f62190784ac.png)