Verlet integration

From Wikipedia, the free encyclopedia

Verlet integration (IPA: [veʁ'le]) is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and video games. The verlet integrator offers greater stability than the much simpler Euler method, as well as other properties that are important in physical systems such as time-reversibility and area preserving properties. At first it may seem natural to simply calculate trajectories using Euler integration. However, this kind of integration suffers from many problems, as discussed at Euler integration. Stability of the technique depends fairly heavily upon either a uniform update rate, or the ability to accurately identify positions at a small time delta into the past. The method was used by Carl Størmer to compute the trajectories of particles moving in a magnetic field (hence it is also called Störmer's method) and was popularized in molecular dynamics by French physicist Loup Verlet in 1967.

[edit] Basic Verlet

The Verlet algorithm [1] reduces the level of errors introduced into the integration by calculating the position at the next time step from the positions at the previous and current time steps, without using the velocity. It is derived by writing two Taylor expansions of the position vector $\vec{x}(t)$ in different time directions.

$\vec{x}(t + \Delta t) = \vec{x}(t) + \vec{v}(t)\Delta t + \frac{\vec{a}(t) \Delta t^2}{2} + \frac{\vec{b}(t) \Delta t^3}{6} + O(\Delta t^4)\,$

$\vec{x}(t - \Delta t) = \vec{x}(t) - \vec{v}(t)\Delta t + \frac{\vec{a}(t) \Delta t^2}{2} - \frac{\vec{b}(t) \Delta t^3}{6} + O(\Delta t^4).\,$

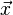Where $\vec{x}$ is the position, 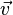$\vec{v}$ the velocity, 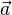$\vec{a}$ the acceleration and $\vec{b}$ the jerk (third derivative of the position with respect to the time) $t$ . Adding these two expansions gives

$\vec{x}(t + \Delta t) = 2\vec{x}(t) - \vec{x}(t - \Delta t) + \vec{a}(t) \Delta t^2 + O(\Delta t^4).\,$

This offers the advantage that the first and third-order term from the Taylor expansion cancels out, thus making the Verlet integrator an order more accurate than integration by simple Taylor expansion alone. Note that if using this equation at $t = 0$ , one needs the position at time $- Δ t$ , $\vec{x}(-\Delta t)$ . At first sight this could give problems, because the initial conditions are known only at the initial time. This can be solved by doing the first time step using the equation

$\vec{x}(\Delta t) \approx \vec{x}(0) + \vec{v}(0)\Delta t + \frac{\vec{a}(0)\Delta t^2}{2} + O(\Delta t^3).\,$

The error on the first time step calculation then is of $Δ t 3$ order. This is not considered a problem because on a simulation of over a large amount of timesteps, the error on the first timestep is only a negligible small amount of the total error. As also can be seen in the basic verlet formula, the velocities are not explicitly given in the Basic Verlet equation, but often they are necessary for the calculation of certain physical quantities. This can create technical challenges in molecular dynamics simulations, because kinetic energy and instantaneous temperatures at time $t$ cannot be calculated for a system until the positions are known at time $t + Δ t$ . This deficiency can either be dealt with using the Velocity Verlet algorithm, or estimating the velocity using the position terms and the mean value theorem:

$\vec{v}(t) = \frac{\vec{x}(t + \Delta t) - \vec{x}(t - \Delta t)}{2\Delta t} + O(\Delta t^2).$

Note that this velocity term is for the velocity at time $t$ , not $t + Δ t$ , meaning that the velocity term is a step behind the position term. You can shorten the interval to approximate the velocity at time $t + Δ t$ at the cost of accuracy:

$\vec{v}(t + \Delta t) = \frac{\vec{x}(t + \Delta t) - \vec{x}(t)}{\Delta t} + O(\Delta t).$

[edit] Velocity Verlet

A related, and more commonly used, algorithm is the Velocity Verlet algorithm [2]. This uses a similar approach but explicitly incorporates velocity, solving the first-timestep problem in the Basic Verlet algorithm:

$\vec{x}(t + \Delta t) = \vec{x}(t) + \vec{v}(t)\, \Delta t + \frac{1}{2} \vec{a}(t) (\Delta t)^2 \,$

$\vec{v}(t + \Delta t) = \vec{v}(t) + \frac{\vec{a}(t) + \vec{a}(t + \Delta t)}{2} \Delta t \,$

It can be shown that the error on the Velocity Verlet is of the same order as the Basic Verlet. Note that the Velocity algorithm is not necessarily more memory consuming, because it's not necessary to keep track of the velocity at every timestep during the simulation. The standard implementation scheme of this algorithm is:

Calculate: $\vec{x}(t + \Delta t) = \vec{x}(t) + \vec{v}(t)\, \Delta t + \frac{1}{2} \vec{a}(t) (\Delta t)^2 \,$
Calculate: $\vec{v}(t + \frac{\Delta t}{2}) = \vec{v}(t) + \frac{\vec{a}(t)\Delta t}{2} \,$
Derive $\vec{a}(t + \Delta t)$ from the interaction potential.
Calculate: $\vec{v}(t + \Delta t) = \vec{v}(t + \frac{\Delta t}{2}) + \frac{\vec{a}(t + \Delta t)\Delta t}{2} \,$

The derivation of the acceleration comes from the relation

$\vec{F} = - \vec{\nabla}V = m \vec{a}\,$

Note, however, that this algorithm assumes that acceleration at time $\vec{a}(t + \Delta t)$ only depends on position $\vec{x}(t + \Delta t)$ , and does not depend on velocity $\vec{v}(t + \Delta t)$

[edit] Error terms

The local error in position of the Verlet integrator is $O (Δ t 4)$ as described above, and the local error in velocity is $O (Δ t 2)$ .

The global error in position, in contrast, is $O (Δ t 2)$ and the global error in velocity is $O (Δ t 2)$ . These can be derived by noting the following:

$\mathrm{error}\bigl(x(t_0 + \Delta t)\bigr) = O(\Delta t^4)$

and

$x(t_0 + 2\Delta t) = 2x(t_0 + \Delta t) - x(t_0) + \Delta t^2 x''(t_0 + \Delta t) + O(\Delta t^4) \,$

Therefore:

$\mathrm{error}\bigl(x(t_0 + 2\Delta t)\bigr) = 2\mathrm{error}\bigl(x(t_0 + \Delta t)\bigr) + O(\Delta t^4) = 3\,O(\Delta t^4)$

Similarly:

$\mathrm{error}\bigl(x(t_0 + 3\Delta t)\bigl) = 6\,O(\Delta t^4)$

$\mathrm{error}\bigl(x(t_0 + 4\Delta t)\bigl) = 10\,O(\Delta t^4)$

$\mathrm{error}\bigl(x(t_0 + 5\Delta t)\bigl) = 15\,O(\Delta t^4)$

Which can be generalized to (it can be shown by induction, but it is given here without proof):

$\mathrm{error}\bigl(x(t_0 + n\Delta t)\bigr) = \frac{n(n+1)}{2}\,O(\Delta t^4)$

If we consider the global error in position between $x (t)$ and $x (t + T)$ , where $T = n Δ t$ , it is clear that:

$\mathrm{error}\bigl(x(t_0 + T)\bigr) = \left(\frac{T^2}{2\Delta t^2} + \frac{T}{2\Delta t}\right) O(\Delta t^4)$

And therefore, the global (cumulative) error over a constant interval of time is given by:

$\mathrm{error}\bigr(x(t_0 + T)\bigl) = O(\Delta t^2)$

Because the velocity is determined in a non-cumulative way from the positions in the Verlet integrator, the global error in velocity is also $O (Δ t 2)$ .

In molecular dynamics simulations, the global error is typically far more important than the local error, and the Verlet integrator is therefore known as a second-order integrator.

[edit] Constraints

Main article: Constraint algorithm

The most notable thing that is now easier due to using Verlet integration rather than Eulerian is that constraints between particles are very easy to do. A constraint is a connection between multiple points that limits them in some way, perhaps setting them at a specific distance or keeping them apart, or making sure they are closer than a specific distance. Often physics systems use springs between the points in order to keep them in the locations they are supposed to be. However, using springs of infinite stiffness between two points usually gives the best results coupled with the verlet algorithm. Here's how:

$d_1=x_2^{(t)}-x_1^{(t)}\,$

$d_2=\|d_1\|\,$

$d_3=\frac{d_2-r}{d_2}\,$

$x_1^{(t+\Delta t)}=\tilde{x}_1^{(t+\Delta t)}+\frac{1}{2}d_1d_3\,$

$x_2^{(t+\Delta t)}=\tilde{x}_2^{(t+\Delta t)}-\frac{1}{2}d_1d_3\,$

The $x_i^{(t)}$ variables are the positions of the points i at time t, the $\tilde{x}_i^{(t)}$ are the unconstrained positions (i.e. the point positions before applying the constraints) of the points i at time t, the d variables are temporary (they are added for optimization as the results of their expressions are needed multiple times), and r is the distance that is supposed to be between the two points. Currently this is in one dimension; however, it is easily expanded to two or three. Simply find the delta (first equation) of each dimension, and then add the deltas squared to the inside of the square root of the second equation (Pythagorean theorem). Then, duplicate the last two equations for the number of dimensions there are. This is where verlet makes constraints simple - instead of say, applying a velocity to the points that would eventually satisfy the constraint, you can simply position the point where it should be and the verlet integrator takes care of the rest.

Problems, however, arise when multiple constraints position a vertex. One way to solve this is to loop through all the vertices in a simulation in a criss cross manner, so that at every vertex the constraint relaxation of the last vertex is already used speed up the spread of the information. Either use fine time steps for the simulation, use a fixed number of constraint solving steps per time step, or solve constrains until they are met by a specific deviation.

When approximating the constraints locally to first order this is the same as the Gauss–Seidel method. For small matrices it is known that LU decomposition is faster. Large systems can be divided into clusters (for example: each ragdoll=cluster). Inside clusters the LU method is used, between clusters the Gauss–Seidel method is used. The matrix code can be reused: The dependency of the forces on the positions can be approximated locally to first order, and the verlet integration can be made more implicit.

For big matrices sophisticated solvers (look especially for "The sizes of these small dense matrices can be tuned to match the sweet spot" in [3]) for sparse matrices exist, any self made Verlet integration has to compete with these. The usage of (clusters of) matrices is not generally more precise or stable, but addresses the specific problem, that a force on one vertex of a sheet of cloth should reach any other vertex in a low number of time steps even if a fine grid is used for the cloth [4] (link needs refinement) and not form a sound wave.

Another way to solve Holonomic constraints is to use constraint algorithms.

[edit] Collision reactions

One way of reacting to collisions is to use a penalty-based system which basically applies a set force to a point upon contact. The problem with this is that it is very difficult to choose the force imparted. Use too strong a force and objects will become unstable, too weak and the objects will penetrate each other. Another way is to use projection collision reactions which takes the offending point and attempts to move it the shortest distance possible to move it out of the other object.

The Verlet integration would automatically handle the velocity imparted via the collision in the latter case, however note that this is not guaranteed to do so in a way that is consistent with collision physics (that is, changes in momentum are not guaranteed to be realistic). Instead of implicitly changing the velocity term, you would need to explicitly control the final velocities of the objects colliding (by changing the recorded position from the previous time step).

The two simplest methods for deciding on a new velocity are perfectly elastic collisions and inelastic collisions. A slightly more complicated strategy that offers more control would involve using the coefficient of restitution.

[edit] Applications

The Verlet equations can also be modified to create a very simple damping effect (for instance, to emulate air friction in computer games):

$x(t + \Delta t) = (2-f) x(t) -(1-f) x(t - \Delta t) + a(t)(\Delta t)^2.\,$

Where f is a number representing the fraction of the velocity per update that is lost to friction (0-1).

[edit] See also

[edit] External links

Verlet integration

From Wikipedia, the free encyclopedia

Contents

[edit] Basic Verlet

[edit] Velocity Verlet

[edit] Error terms

[edit] Constraints

[edit] Collision reactions

[edit] Applications

[edit] See also

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages