Discrete wavelet transform

From Wikipedia, the free encyclopedia

Jump to: navigation, search
An example of the 2D discrete wavelet transform that is used in JPEG2000. The original image is high-pass filtered, yielding the three large images, each describing local changes in brightness (details) in the original image. It is then low-pass filtered and downscaled, yielding an approximation image; this image is high-pass filtered to produce the three smaller detail images, and low-pass filtered to produce the final approximation image in the upper-left.

In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled.

The first DWT was invented by the Hungarian mathematician Alfréd Haar. For an input represented by a list of 2n numbers, the Haar wavelet transform may be considered to simply pair up input values, storing the difference and passing the sum. This process is repeated recursively, pairing up the sums to provide the next scale: finally resulting in 2n − 1 differences and one final sum.

This simple DWT illustrates the desirable properties of wavelets in general. First, it can be performed in O(n) operations; second, it captures not only a notion of the frequency content of the input, by examining it at different scales, but also temporal content, i.e. the times at which these frequencies occur. Combined, these two properties make the Fast wavelet transform (FWT) an alternative to the conventional Fast Fourier Transform (FFT).

The most commonly used set of discrete wavelet transforms was formulated by the Belgian mathematician Ingrid Daubechies in 1988. This formulation is based on the use of recurrence relations to generate progressively finer discrete samplings of an implicit mother wavelet function; each resolution is twice that of the previous scale. In her seminal paper, Daubechies derives a family of wavelets, the first of which is the Haar wavelet. Interest in this field has exploded since then, and many variations of Daubechies' original wavelets were developed.

Other forms of discrete wavelet transform include the non- or undecimated wavelet transform (where downsampling is omitted), the Newland transform (where an orthonormal basis of wavelets is formed from appropriately constructed top-hat filters in frequency space). Wavelet packet transforms are also related to the discrete wavelet transform. Complex wavelet transform is another form.

The discrete wavelet transform has a huge number of applications in science, engineering, mathematics and computer science. Most notably, it is used for signal coding, to represent a discrete signal in a more redundant form, often as a preconditioning for data compression.

Contents

[edit] Definition

[edit] One level of the transform

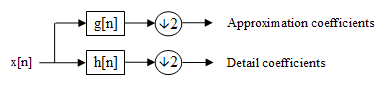
The DWT of a signal x is calculated by passing it through a series of filters. First the samples are passed through a low pass filter with impulse response g resulting in a convolution of the two:

y[n] = (x * g)[n] = \sum\limits_{k = - \infty }^\infty {x[k] g[n - k]}.

The signal is also decomposed simultaneously using a high-pass filter h. The outputs giving the detail coefficients (from the high-pass filter) and approximation coefficients (from the low-pass). It is important that the two filters are related to each other and they are known as a quadrature mirror filter.

However, since half the frequencies of the signal have now been removed, half the samples can be discarded according to Nyquist’s rule. The filter outputs are then subsampled by 2 (It should be noted that Mallat's and the common notation is the opposite, g- high pass and h- low pass):

y_{\mathrm{low}} [n] = \sum\limits_{k = - \infty }^\infty {x[k] g[2 n - k]}
y_{\mathrm{high}} [n] = \sum\limits_{k = - \infty }^\infty {x[k] h[2 n - k]}

This decomposition has halved the time resolution since only half of each filter output characterises the signal. However, each output has half the frequency band of the input so the frequency resolution has been doubled.

Block diagram of filter analysis


With the subsampling operator \downarrow

(y \downarrow k)[n] = y[k n]

the above summation can be written more concisely.

y_{\mathrm{low}} = (x*g)\downarrow 2
y_{\mathrm{high}} = (x*h)\downarrow 2

However computing a complete convolution x * g with subsequent downsampling would waste computation time.

The Lifting scheme is an optimization where these two computations are interleaved.

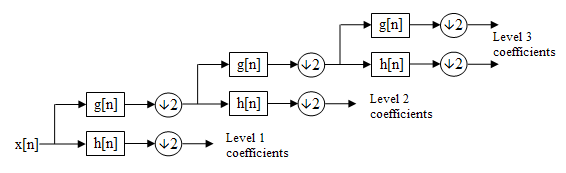
[edit] Cascading and Filter banks

This decomposition is repeated to further increase the frequency resolution and the approximation coefficients decomposed with high and low pass filters and then down-sampled. This is represented as a binary tree with nodes representing a sub-space with a different time-frequency localisation. The tree is known as a filter bank.

A 3 level filter bank

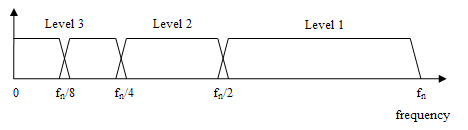
At each level in the above diagram the signal is decomposed into low and high frequencies. Due to the decomposition process the input signal must be a multiple of 2n where n is the number of levels.

For example a signal with 32 samples, frequency range 0 to fn and 3 levels of decomposition, 4 output scales are produced:

Level Frequencies Samples
3 0 to fn / 8 4
fn / 8 to fn / 4 4
2 fn / 4 to fn / 2 8
1 fn / 2 to fn 16
Frequency domain representation of the DWT

[edit] Code examples

In its simplest form, the DWT is remarkably easy to compute.

The Haar wavelet in Java:

public static int[] invoke(int[] input)
{
 
    //This function assumes input.length=2^n, n>1
    int[] output = new int[input.length];
 
    for (int length = input.length >> 1; ; length >>= 1) {
        //length=2^n, WITH DECREASING n
        for (int i = 0; i < length; i++) {
            int sum = input[i*2]+input[i*2+1];
            int difference = input[i*2]-input[i*2+1];
            output[i] = sum;
            output[length+i] = difference;
        }
        if (length == 1) 
            return output;
 
        //Swap arrays to do next iteration
        System.arraycopy(output, 0, input, 0, length<<1);
    }
}

A fast lifting implementation of the discrete biorthogonal CDF 9/7 wavelet transform in C language, used in the JPEG-2000 image compression standard can be found here.

[edit] See also

[edit] References

Retrieved from "http://en.wikipedia.org/wiki/Discrete_wavelet_transform"
Personal tools