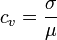Coefficient of variation

From Wikipedia, the free encyclopedia

In probability theory and statistics, the coefficient of variation (CV) is a normalized measure of dispersion of a probability distribution. It is defined as the ratio of the standard deviation $\ \sigma$ to the mean $\ \mu$ :

$c_v = {\sigma \over \mu }$

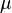This is only defined for non-zero mean, and is most useful for variables that are always positive. It is also known as unitized risk.

The coefficient of variation should only be computed for data measured on a ratio scale. It does not have any meaning for data on an interval scale.^[1]

Standardized moments are similar ratios, $\frac{\mu_k}{\sigma^k}$ , which are also dimensionless and scale invariant. The variance-to-mean ratio, $σ 2 / μ$ , is another similar ratio, but is not dimensionless, and hence not scale invariant.

See Normalization (statistics) for further ratios.

In signal processing, particularly image processing, the reciprocal ratio $μ / σ$ is referred to as the signal to noise ratio.

[edit] Comparison to standard deviation

[edit] Advantages

The coefficient of variation is useful because the standard deviation of data must always be understood in the context of the mean of the data. The coefficient of variation is a dimensionless number. So when comparing between data sets with different units or wildly different means, one should use the coefficient of variation for comparison instead of the standard deviation.

[edit] Disadvantages

When the mean value is near zero, the coefficient of variation is sensitive to small changes in the mean, limiting its usefulness.
Unlike the standard deviation, it cannot be used to construct confidence intervals for the mean.

[edit] Applications

The coefficient of variation is also common in applied probability fields such as renewal theory, queueing theory, and reliability theory. In these fields, the exponential distribution is often more important than the normal distribution. The standard deviation of an exponential distribution is equal to its mean, so its coefficient of variation is equal to 1. Distributions with CV < 1 (such as an Erlang distribution) are considered low-variance, while those with CV > 1 (such as a hyper-exponential distribution) are considered high-variance. Some formulas in these fields are expressed using the squared coefficient of variation, often abbreviated SCV. In modeling, a variation of the CV is the CV(RMSD). Essentially the CV(RMSD) replaces the standard deviation term with the Root Mean Square Deviation (RMSD).