VC dimension
From Wikipedia, the free encyclopedia
In statistical learning theory, or sometimes computational learning theory, the VC dimension (for Vapnik-Chervonenkis dimension) is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter. It is a core concept in Vapnik-Chervonenkis theory, and was originally defined by Vladimir Vapnik and Alexey Chervonenkis.
Informally, the capacity of a classification model is related to how complicated it can be. For example, consider the thresholding of a high-degree polynomial: if the polynomial evaluates above zero, that point is classified as positive, otherwise as negative. A high-degree polynomial can be wiggly, so it can fit a given set of training points well. But one can expect that the classifier will make errors on other points, because it is too wiggly. Such a polynomial has a high capacity. A much simpler alternative is to threshold a linear function. This polynomial may not fit the training set well, because it has a low capacity. We make this notion of capacity more rigorous below.
[edit] Shattering
A classification model f with some parameter vector θ is said to shatter a set of data points (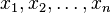
) if, for all assignments of labels to those points, there exists a θ such that the model f makes no errors when evaluating that set of data points.
VC dimension of a model f is h' where h' is the maximum h such that some data point set of cardinality h can be shattered by f.
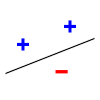
For example, consider a straight line as the classification model: the model used by a perceptron. The line should separate positive data points from negative data points. There exists some set of 3 points that can be shattered using this model (indeed, any 3 points that are not collinear can be shattered). However, no set of 4 points can be shattered. Thus, the VC dimension of this particular classifier is 3. It is important to remember that one can choose the arrangement of points, but then cannot change it as the labels on the points are considered. Note, only 3 of the 23 = 8 possible label assignments are shown for the 3 points.
 |
 |
 |
 |
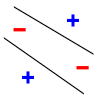| 3 points shattered | 4 points impossible | ||
[edit] Uses
The VC dimension has utility in statistical learning theory, because it can predict a probabilistic upper bound on the test error of a classification model.
The bound on the test error of a classification model (on data that is drawn i.i.d. from the same distribution as the training set) is given by
- Training error +
with probability 1 − η, where h is the VC dimension of the classification model, and N is the size of the training set (restriction: this formula is valid when the VC dimension is small h < N). Similar complexity bounds can be derived using Rademacher complexity, but Rademacher complexity can sometimes provide more insight than VC dimension calculations into such statistical methods such as those using kernels.
[edit] References
- Andrew Moore's VC dimension tutorial
- V. Vapnik and A. Chervonenkis. "On the uniform convergence of relative frequencies of events to their probabilities." Theory of Probability and its Applications, 16(2):264--280, 1971.
- A. Blumer, A. Ehrenfeucht, D. Haussler, and M. K. Warmuth. "Learnability and the Vapnik-Chervonenkis dimension." Journal of the ACM, 36(4):929--865, 1989.
- Christopher Burges Tutorial on SVMs for Pattern Recognition (containing information also for VC dimension) [1]
