Octree

From Wikipedia, the free encyclopedia

Please help improve this article or section by expanding it. Further information might be found on the talk page. (April 2009)

Left: Recursive subdivision of a cube into octants. Right: The corresponding octree.

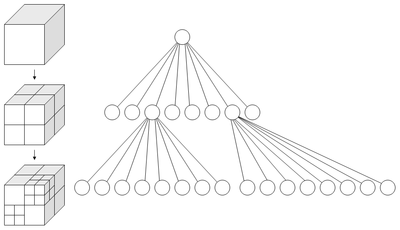
An octree is a tree data structure in which each internal node has up to eight children. Octrees are most often used to partition a three dimensional space by recursively subdividing it into eight octants. Octrees are the three-dimensional analog of quadtrees. The name is formed from oct + tree, and normally written "octree", not "octtree".

[edit] Octrees for spatial representation

Each node in an octree subdivides the space it represents into eight octants. In a point region (PR) octree, the node stores an explicit 3-dimensional point, which is the "center" of the subdivision for that node; the point defines one of the corners for each of the eight children. In an MX octree, the subdivision point is implicitly the center of the space the node represents. The root node of a PR octree can represent infinite space; the root node of an MX octree must represent a finite bounded space so that the implicit centers are well-defined. Octrees are never considered kD-trees, as kD-trees split along a dimension and octrees split around a point. kD-trees are also always binary, which is not true of octrees.

[edit] Common uses of octrees

• Spatial indexing
• Efficient collision detection in three dimensions
• View frustum culling
• Fast Multipole Method
• Unstructured grid
• Finite element analysis

[edit] Application to color quantization

The octree color quantization algorithm, invented by Gervautz and Purgathofer in 1988, encodes image color data as an octree up to nine levels deep. Octrees are used because 2³ = 8 and there are three color components in the RGB system. The node index to branch out from at the top level is determined by a formula that uses the most significant bits of the red, green, and blue color components, e.g. 4r + 2g + b. The next lower level uses the next bit significance, and so on. Less significant bits are sometimes ignored to reduce the tree size.

The algorithm is highly memory efficient because the tree's size can be limited. The bottom level of the octree consists of leaf nodes that accrue color data not represented in the tree; these nodes initially contain single bits. If much more than the desired number of palette colors are entered into the octree, its size can be continually reduced by seeking out a bottom-level node and averaging its bit data up into a leaf node, pruning part of the tree. Once sampling is complete, exploring all routes in the tree down to the leaf nodes, taking note of the bits along the way, will yield approximately the required number of colors.

[edit] See also

• Quadtree
• kd-tree
• Loose octrees
• Bounding Interval Hierarchy
• Klee's measure problem
• Linear octrees
• Balanced octrees
• Sauerbraten, a 3D game engine in which geometry is almost entirely based on octrees
• OGRE, has an Octree Scene Manager Implementation
• Dendro, a parallel multigrid library for finite element computations using octrees

[edit] External links

• Octree Quantization in Microsoft Systems Journal
• Color Quantization using Octrees in Dr. Dobb's
• Color Quantization using Octrees in Dr. Dobb's Source Code
• Octree Overview
• Parallel implementation of octtree generation algorithm, P. Sojan Lal, A Unnikrishnan, K Poulose Jacob, ICIP 1997, IEEE Digital Library
• Generation of Octrees from Raster Scan with Reduced Information Loss, P. Sojan Lal, A Unnikrishnan, K Poulose Jacob, IASTED International conference VIIP 2001 [1]
• C++ implementation (GPL license)
• Parallel Octrees for Finite Element Applications
• Sauerbraten - a game written in the octree-heavy Cube 2 engine
• Ogre - A 3d Object-oriented Graphics Rendering Engine with a Octree Scene Manager Implementation (LGPL license)
• Dendro: parallel multigrid for octree meshes (MPI/C++ implementation)