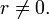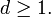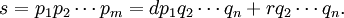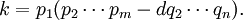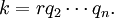algebra arithmatics arithmetic dsa frompaul interests math math201 mathematics maths prime_no. spy101

My tags:

From Wikipedia, the free encyclopedia

In number theory and algebraic number theory, the Fundamental Theorem of Arithmetic (or Unique-Prime-Factorization Theorem) states that any integer greater than 1 can be written as a unique product (up to ordering of the terms) of prime numbers. For example,

are two examples of numbers satisfying the hypothesis of the theorem, that can be written as the product of prime numbers. Intuitively, this theorem characterizes prime numbers uniquely in the sense that they are the "core of all numbers".

Proof of existence of a prime factorization is relatively straightforward: proof of the uniqueness uniqueness (up to rearrangement of the terms) is more challenging. Some proofs of uniqueness use the fact that if a prime number p divides the product of two natural numbers a and b, then p divides either a or b, a statement known as Euclid's lemma. Since multiplication on the integers is both commutative and associative, it does not matter in what way we write a number greater than 1 as the product of primes; it is generally common to write the (prime) factors in the order of smallest to largest.

There are natural extensions of the hypothesis of this theorem, which allow any non-zero integer to be expressed as the product of "prime numbers" and "invertibles". For example, 1 and -1 are allowed to be factors of such representations (although they are not considered to be prime). In this way, one can extend the Fundamental Theorem of Arithmetic to any Euclidean domain or principal ideal domain bearing in mind certain alterations to the hypothesis of the theorem. A ring in which the Fundamental Theorem of Arithmetic holds, is called a unique factorization domain.

Many authors take the natural numbers to begin with 0, which has no prime factorization. Thus Theorem 1 of Hardy & Wright (1979) takes the form, “Every positive integer, except 1, is a product of primes”, and Theorem 2 (their "Fundamental") asserts uniqueness. By convention, the number 1 is not itself prime, but since it is the product of no numbers, it is often convenient to include it in the theorem by the empty product rule. (See, for example, Calculating the gcd.)

Hardy & Wright define an abnormal number to be a hypothetical number that does not have a unique prime factorization. They prove the fundamental theorem of arithmetic by proving that there does not exist an abnormal number.

Contents 1 Applications 2 Proof 2.1 Euclid's proof (of existence) 2.1.1 Non-prime composite numbers 2.2 Proof of uniqueness 2.3 Alternate proof 3 Generalizations 4 See also 5 References 6 External links

[edit] Applications

The fundamental theorem of arithmetic establishes the importance of prime numbers. Prime numbers are the basic building blocks of any positive integer, in the sense that each positive integer can be constructed from the product of primes with one unique construction. Finding the prime factorization of an integer allows derivation of all its divisors, both prime and non-prime.

For example, the above factorization of 6936 shows that any positive divisor of 6936 must have the form 2^a × 3^b  × 17^c, where a takes one of the 4 values in {0, 1, 2, 3}, where b takes one of the 2 values in {0, 1}, and where c takes one of the 3 values in {0, 1, 2}. Multiplying the numbers of independent options together produces a total of 4 × 2 × 3 = 24 positive divisors.

Once the prime factorizations of two numbers are known, their greatest common divisor and least common multiple can be found quickly. For instance, from the above it is shown that the greatest common divisor of 6936 and 1200 is 2³ × 3 = 24. However, if the prime factorizations are not known, the use of the Euclidean algorithm generally requires much less calculation than factoring the two numbers.

The fundamental theorem ensures that additive and multiplicative arithmetic functions are completely determined by their values on the powers of prime numbers.

[edit] Proof

The theorem was practically proved by Euclid (in book 7 of Euclid's elements, propositions 30 and 32), but the first full and correct proof is found in the Disquisitiones Arithmeticae by Carl Friedrich Gauss. It may be important to note that Egyptians like Ahmes used earlier practical aspects of the factoring, and lowest common multiple, of the fundamental theorem of arithmetic allowing a long tradition to develop, as formalized by Euclid, and rigorously proven by Gauss.

Although at first sight the theorem seems 'obvious', it does not hold in more general number systems, including many rings of algebraic integers. This was first pointed out by Ernst Kummer in 1843, in his work on Fermat's Last Theorem. The recognition of this failure is one of the earliest developments in algebraic number theory.

[edit] Euclid's proof (of existence)

The proof consists of two steps. In the first step every number is shown to be a product of zero or more primes. In the second, the proof shows that any two representations may be unified into a single representation.

[edit] Non-prime composite numbers

Suppose there were a positive integer which cannot be written as a product of primes. Then there must be a smallest such number (see well-order): let it be n. This number n cannot be 1, because of the empty-product convention above. It cannot be a prime number either, since any prime number is a product of a single prime, itself. So it must be a composite number. Thus

n = ab

where both a and b are positive integers smaller than n. Since n is the smallest number which cannot be written as a product of primes, both a and b can be written as products of primes. But then

n = ab

can be written as a product of primes as well, a proof by contradiction. This is a minimal counterexample argument.

[edit] Proof of uniqueness

The key step in proving uniqueness is Euclid's proposition 30 of book 7 (known as Euclid's lemma), which states that, for any prime number p and any natural numbers a, b: if p divides ab then either p divides a or p divides b.

This may be proved as follows:

• Suppose that a prime p divides ab (where a, b are natural numbers) but does not divide a. We must prove that p divides b.
• Since p does not divide a, the greatest common divisor of p and a is 1.
• By Bézout's identity, it follows that for some integers x, y (possibly negative),
• Multiplying both sides by b,
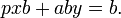
• Since p divides both summands on the left, p divides b.

A proof of the uniqueness of the prime factorization of a given integer proceeds as follows. Let s be the smallest natural number that can be written as (at least) two different products of prime numbers. Denote these two factorizations of s as p₁···p_m and q ₁···q_n, such that s = p₁p₂···p_m = q ₁q₂···q_n. By Euclid's proposition either p₁ divides q₁, or p₁ divides q ₂···q_n. Both q₁ and q ₂···q_n must have unique prime factorizations (since both are smaller than s), and thus p₁  =  q_j (for some j). But by removing p₁ and q_j from the initial equivalence we have a smaller integer factorizable in two ways, contradicting our initial assumption. Therefore there can be no such s, and all natural numbers have a unique prime factorization.

[edit] Alternate proof

Assume that a certain integer s can be written as (at least) two different products of prime numbers. Denote these two factorizations of s as p₁···p_m and q ₁···q_n, such that s = p₁p₂···p_m = q ₁q₂···q_n.

No p_i (with 1 ≤ i ≤ m) can be equal to any q_j (with 1 ≤ j ≤ n), as there would otherwise be a smaller integer factorizable in two ways (by removing prime factors common in both products), violating the above assumption. Now it can be assumed without loss of generality that p₁ is a prime factor smaller than any q _j (with 1 ≤ j ≤ n). Let d be the quotient and r the remainder from dividing q ₁ by p₁. By the division algorithm d and r are guaranteed to be integers such that q ₁ = dp₁ + r and 0 ≤ r < p₁. Note immediately that since q ₁ is prime it cannot be a multiple of p₁ and thus

Also, since q₁ is greater than p₁

Substituting in for q₁ in the original definition of s above,

By distributivity:

Define a new integer k = s −dp₁q₂···q_n = rq₂···q_n. Since d≥ 1, it is clear that k must be smaller than s. And since r>0, k must be positive. From the definition of k, it follows that:

and by factoring out p₁:

Therefore there is a prime factorization of k that includes p₁. But it is also true that

Since r < p₁, p₁ cannot be a prime factor of r. Thus, by combining the prime factors of r with q₂···q_n, it is also possible to construct a prime factorization of k that does not include p₁. Therefore k has two different prime factorizations. However, an even smaller number than k must exist with more than one prime factorization by the same reasoning. This gives an infinite descent of such numbers, which is impossible because there are no positive integers for which there are an infinite number of smaller positive integers. Thus there can exist no such numbers.

[edit] Generalizations

The Fundamental Theorem of Arithmetic generalizes to various contexts; for example in the context of ring theory, where the field of algebraic number theory develops. A ring is said to be a unique factorization domain if the Fundamental theorem of arithmetic (for non-zero elements) holds there. For example, any Euclidean domain or principal ideal domain is necessarily a unique factorization domain. Specifically, a field is trivially a unique factorization domain.

[edit] See also

• Fundamental theorem of algebra
• Fundamental theorem of calculus
• Integer factorization
• Prime signature
• Unique factorization domain

[edit] References

• Hardy, G. H.; Wright, E. M. (1979), An Introduction to the Theory of Numbers (fifth ed.), USA: Oxford University Press, ISBN 978-0-19-853171-5 
• Baker, Alan (1984), A Concise Introduction to the Theory of Numbers, Cambridge, UK: Cambridge University Press, ISBN 978-0-521-28654-1 
• Eric W. Weisstein, Abnormal number at MathWorld.
• Eric W. Weisstein, Fundamental Theorem of Arithmetic at MathWorld.

[edit] External links

• GCD and the Fundamental Theorem of Arithmetic at cut-the-knot
• PlanetMath: Proof of fundamental theorem of arithmetic
• Fermat's Last Theorem Blog: Unique Factorization, A blog that covers the history of Fermat's Last Theorem from Diophantus of Alexandria to the proof by Andrew Wiles.
• "Fundamental Theorem of Arithmetic" by Hector Zenil, Wolfram Demonstrations Project, 2007.

v • d • e Fundamental mathematical theorems Arithmetic · Algebra · Calculus · Linear algebra · Calculus of variations · Vector analysis · Homomorphisms · Galois theory Geometric Projective · Riemannian · Curves of Groups Cyclic · Finitely-generated Abelian