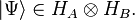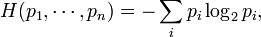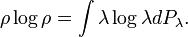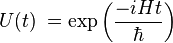Quantum entanglement

	Quantum mechanics
	Uncertainty principle;
Background
	Classical mechanics; Old quantum theory; Interference · Bra-ket notation; Hamiltonian
Fundamental concepts
	Quantum state · Wave function; Superposition · Entanglement; Measurement · Uncertainty; Exclusion · Duality; Decoherence · Ehrenfest theorem · Tunneling
Experiments
	Double-slit experiment; Davisson–Germer experiment; Stern–Gerlach experiment; Bell's inequality experiment; Popper's experiment; Schrödinger's cat; Elitzur-Vaidman bomb-tester; Quantum eraser
Formulations
	Schrödinger picture; Heisenberg picture; Interaction picture; Matrix mechanics; Sum over histories
Equations
	Schrödinger equation; Pauli equation; Klein–Gordon equation; Dirac equation; Bohr Theory and Balmer-Rydberg Equation
Interpretations
	Copenhagen · Ensemble; Hidden variable theory · Transactional; Many-worlds · Consistent histories; Relational · Quantum logic · Pondicherry
Advanced topics
	Quantum field theory; Quantum gravity; Theory of everything
Scientists
	Planck · Einstein · Bohr · Sommerfeld · Bose · Kramers · Heisenberg· Born · Jordan · Pauli · Dirac · de Broglie ·Schrödinger · von Neumann · Wigner · Feynman · Candlin · Bohm · Everett · Bell · Wien
	This box: view • talk • edit

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Quantum entanglement is a possible property of a quantum mechanical state of a system of two or more objects in which the quantum states of the constituting objects are linked together so that one object can no longer be adequately described without full mention of its counterpart — even though the individual objects may be spatially separated. This interconnection leads to non-classical correlations between observable physical properties of remote systems, often referred to as nonlocal correlations. For example, quantum mechanics holds that states such as spin are indeterminate until such time as some physical intervention is made to measure the spin of the object in question. It is equally likely that any given particle will be observed to be spin-up as that it will be spin-down. Measuring any number of particles will result in an unpredictable series of measures that will tend more and more closely to half up and half down. However, if this experiment is done with entangled particles the results are quite different. When two members of an entangled pair are measured, one will always be spin-up and the other will be spin-down.^{[citation needed]} The distance between the two particles is irrelevant. Theories involving 'hidden variables' have been proposed in order to explain this result; these hidden variables account for the spin of each particle, and are determined when the entangled pair is created. It may appear then that the hidden variables must be in communication no matter how far apart the particles are, that the hidden variable describing one particle must be able to change instantly when the other is measured. If the hidden variables stop interacting when they are far apart, the statistics of multiple measurements must obey an inequality (called Bell's inequality), which is, however, violated — both by quantum mechanical theory and in experiments.^{[citation needed]}

When pairs of particles are generated by the decay of other particles, naturally or through induced collision, these pairs may be termed "entangled", in that such pairs often necessarily have linked and opposite qualities, i.e. of spin or charge. The assumption that measurement in effect "creates" the state of the measured quality goes back to the arguments of, among others: Schrödinger, and Einstein, Podolsky, and Rosen^{[citation needed]} (see EPR paradox) concerning Heisenberg's uncertainty principle and its relation to observation (see also the Copenhagen interpretation). The analysis of entangled particles by means of Bell's theorem, can lead to an impression of non-locality (that is, that there exists a connection between the members of such a pair that defies both classical and relativistic concepts of space and time). This is reasonable if it is assumed that each particle departs the scene of the pair's creation in an ambiguous state (as per a possible interpretation of Heisenberg). In such case, either dichotomous outcome of a given measurement remains a possibility; only measurement itself would precipitate a distinct value. On the other hand, if each particle departs the scene of its "entangled creation" with properties that would unambiguously determine the value of the quality to be subsequently measured, then a postulated instantaneous transmission of information across space and time would not be required to account for the result. The Bohm interpretation postulates that a guide wave exists connecting what are perceived as individual particles such that the supposed hidden variables are actually the particles themselves existing as functions of that wave.

Observation of wavefunction collapse can lead to the impression that measurements performed on one system instantaneously influence other systems entangled with the measured system, even when far apart. Yet another interpretation of this phenomenon is that quantum entanglement does not necessarily enable the transmission of classical information faster than the speed of light because a classical information channel is required to complete the process.^{[citation needed]}

[edit] Background

Entanglement is one of the properties of quantum mechanics that caused Einstein and others to dislike the theory. In 1935, Einstein, Podolsky, and Rosen formulated the EPR paradox, a quantum-mechanical thought experiment with a highly counterintuitive and apparently nonlocal outcome, in response to Niels Bohr's advocacy of the belief that quantum mechanics as a theory was complete.^[1] Einstein famously derided entanglement as "spukhafte Fernwirkung"^{[citation needed]} or "spooky action at a distance". It was his belief that future mathematicians would discover that quantum entanglement entailed nothing more or less than an error in their calculations. As he once wrote: "I find the idea quite intolerable that an electron exposed to radiation should choose of its own free will, not only its moment to jump off, but also its direction. In that case, I would rather be a cobbler, or even an employee in a gaming house, than a physicist".^{[citation needed]}

On the other hand, quantum mechanics has been highly successful in producing correct experimental predictions, and the strong correlations predicted by the theory of quantum entanglement have now in fact been observed.^{[citation needed]} One apparent way to explain found correlations in line with the predictions of quantum entanglement is an approach known as "local hidden variable theory", in which unknown, shared, local parameters would cause the correlations. However, in 1964 John Stewart Bell derived an upper limit, known as Bell's inequality, on the strength of correlations for any theory obeying "local realism". Quantum entanglement can lead to stronger correlations that violate this limit, so that quantum entanglement is experimentally distinguishable from a broad class of local hidden-variable theories.^{[citation needed]} Results of subsequent experiments have overwhelmingly supported quantum mechanics. However, there may be experimental problems, known as "loopholes", that affect the validity of these experimental findings. High-efficiency and high-visibility experiments are now in progress^[specify] that should confirm or invalidate the existence of those loopholes. For more information, see the article on experimental tests of Bell's inequality.

Observations pertaining to entangled states appear to conflict with the property of relativity that information cannot be transferred faster than the speed of light. Although two entangled systems appear to interact across large spatial separations, the current state of belief is that no useful information can be transmitted in this way, meaning that causality cannot be violated through entanglement. This is the statement of the no-communication theorem.

Even if information cannot be transmitted through entanglement alone, it is believed^[who?] that it is possible to transmit information using a set of entangled states used in conjunction with a classical information channel. This process is known as quantum teleportation. Despite its name, quantum teleportation may still not permit information to be transmitted faster than light, because a classical information channel is required to complete the process.

In addition experiments are underway to see if entanglement is the result of retrocausality.^[2]^[3]

[edit] Pure states

The following discussion builds on the theoretical framework developed in the articles bra-ket notation and mathematical formulation of quantum mechanics.^{[citation needed]}

Consider two noninteracting systems $A$ and $B$ , with respective Hilbert spaces $H A$ and $H B$ . The Hilbert space of the composite system is the tensor product

$H_A \otimes H_B .$

If the first system is in state 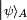$|\scriptstyle \psi \rangle_A$ and the second in state $|\scriptstyle \phi \rangle_B$ , the state of the composite system is

$|\psi\rangle_A \otimes |\phi\rangle_B.$

States of the composite system which can be represented in this form are called separable states, or product states.

Not all states are product states. Fix a basis 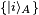$\scriptstyle \{|i \rangle_A\}$ for $H A$ and a basis 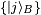$\scriptstyle \{|j \rangle_B\}$ for $H B$ . The most general state in 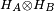$\scriptstyle H_A \otimes H_B$ is of the form

$|\psi\rangle_{AB} = \sum_{i,j} c_{ij} |i\rangle_A \otimes |j\rangle_B$ .

This state is separable if 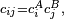$\scriptstyle c_{ij}= c^A_ic^B_j,$ yielding 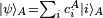$\scriptstyle |\psi\rangle_A = \sum_{i} c^A_{i} |i\rangle_A$ and $\scriptstyle |\phi\rangle_B = \sum_{j} c^B_{j} |j\rangle_B.$ It is inseparable if $\scriptstyle c_{ij} \neq c^A_ic^B_j.$ If a state is inseparable, it is called an entangled state.

For example, given two basis vectors 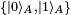$\scriptstyle \{|0\rangle_A, |1\rangle_A\}$ of $H A$ and two basis vectors 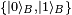$\scriptstyle \{|0\rangle_B, |1\rangle_B\}$ of $H B$ , the following is an entangled state:

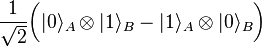${1 \over \sqrt{2}} \bigg( |0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B \bigg)$ .

If the composite system is in this state, it is impossible to attribute to either system $A$ or system $B$ a definite pure state. Instead, their states are superposed with one another. In this sense, the systems are "entangled".

Now suppose Alice is an observer for system $A$ , and Bob is an observer for system $B$ . If Alice makes a measurement in the $\scriptstyle \{|0\rangle, |1\rangle\}$ eigenbasis of A, there are two possible outcomes, occurring with equal probability:^{[citation needed]}

Alice measures 0, and the state of the system collapses to $\scriptstyle |0\rangle_A |1\rangle_B$ .
Alice measures 1, and the state of the system collapses to $\scriptstyle |1\rangle_A |0\rangle_B$ .

If the former occurs, then any subsequent measurement performed by Bob, in the same basis, will always return 1. If the latter occurs, (Alice measures 1) then Bob's measurement will return 0 with certainty. Thus, system B has been altered by Alice performing a local measurement on system A. This remains true even if the systems A and B are spatially separated. This is the foundation of the EPR paradox.

The outcome of Alice's measurement is random. Alice cannot decide which state to collapse the composite system into, and therefore cannot transmit information to Bob by acting on her system. Causality is thus preserved, in this particular scheme. For the general argument, see no-communication theorem.

In some formal mathematical settings^[specify], it is noted that the correct setting for pure states in quantum mechanics is projective Hilbert space endowed with the Fubini-Study metric. The product of two pure states is then given by the Segre embedding.

[edit] Ensembles

As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space. More generally, if one has a large number of copies of the same system, then the state of this ensemble is described by a density matrix, which is a positive matrix, or a trace class when the state space is infinite dimensional, and has trace 1. Again, by the spectral theorem, such a matrix takes the general form:

$\rho = \sum_i w_i |\alpha_i\rangle \langle\alpha_i|$ ,

where the $w i$ 's sum up to 1, and in the infinite dimensional case, we would take the closure of such states in the trace norm. We can interpret $ρ$ as representing an ensemble where $w i$ is the proportion of the ensemble whose states are 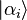$|\alpha_i\rangle$ . When a mixed state has rank 1, it therefore describes a pure ensemble. When there is less than total information about the state of a quantum system we need density matrices to represent the state.

Following the definition in previous section, for a bipartite composite system, mixed states are just density matrices on 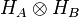$H_A \otimes H_B$ . Extending the definition of separability from the pure case, we say that a mixed state is separable if it can be written as

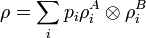$\rho = \sum_i p_i \rho_i^A \otimes \rho_i^B$ ,

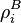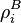where $\rho_i^A$ 's and $\rho_i^B$ 's are they themselves states on the subsystems A and B respectively. In other words, a state is separable if it is probability distribution over uncorrelated states, or product states. We can assume without loss of generality that $\rho_i^A$ and $\rho_i^B$ are pure ensembles. A state is then said to be entangled if it is not separable. In general, finding out whether or not a mixed state is entangled is considered difficult. Formally, it has been shown to be NP-hard. 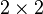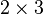For the $2 \times 2$ and $2 \times 3$ cases, a necessary and sufficient criterion for separability is given by the famous Positive Partial Transpose (PPT) condition.

Experimentally, a mixed ensemble might be realized as follows. Consider a "black-box" apparatus that spits electrons towards an observer. The electrons' Hilbert spaces are identical. The apparatus might produce electrons that are all in the same state; in this case, the electrons received by the observer are then a pure ensemble. However, the apparatus could produce electrons in different states. 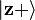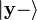For example, it could produce two populations of electrons: one with state $|\mathbf{z}+\rangle$ with spins aligned in the positive $\mathbf{z}$ direction, and the other with state $|\mathbf{y}-\rangle$ with spins aligned in the negative $\mathbf{y}$ direction. Generally, this is a mixed ensemble, as there can be any number of populations, each corresponding to a different state.

[edit] Reduced density matrices

Consider as above systems $A$ and $B$ each with a Hilbert space $H A$ , $H B$ . Let the state of the composite system be

$|\Psi \rangle \in H_A \otimes H_B.$

As indicated above, in general there is no way to associate a pure state to the component system $A$ . However, it still is possible to associate a density matrix. Let

$\rho_T = |\Psi\rangle \; \langle\Psi|$ .

which is the projection operator onto this state. The state of $A$ is the partial trace of $ρ T$ over the basis of system $B$ :

$\rho_A \ \stackrel{\mathrm{def}}{=}\ \sum_j \langle j|_B \left( |\Psi\rangle \langle\Psi| \right) |j\rangle_B = \hbox{Tr}_B \; \rho_T$ .

$ρ A$ is sometimes called the reduced density matrix of $ρ$ on subsystem A. Colloquially, we "trace out" system B to obtain the reduced density matrix on A.

For example, the density matrix of $A$ for the entangled state discussed above is

$\rho_A = (1/2) \bigg( |0\rangle_A \langle 0|_A + |1\rangle_A \langle 1|_A \bigg)$

This demonstrates that, as expected, the reduced density matrix for an entangled pure ensemble is a mixed ensemble. Also not surprisingly, the density matrix of $A$ for the pure product state 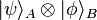$|\psi\rangle_A \otimes |\phi\rangle_B$ discussed above is

$\rho_A = |\psi\rangle_A \langle\psi|_A .$

In general, a bipartite pure state ρ is entangled if and only if one, meaning both, of its reduced states are mixed states.

[edit] Entropy

In this section we briefly discuss entropy of a mixed state and how it can be viewed as a measure of entanglement.

[edit] Definition

In classical information theory, to a probability distribution 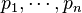$p_1, \cdots, p_n$ , one can associate the Shannon entropy:^{[citation needed]}

$H(p_1, \cdots, p_n ) = - \sum_i p_i \log_2 p_i,$

Since a mixed state ρ is a probability distribution over an ensemble, this leads naturally to the definition of the von Neumann entropy:

$S(\rho) = - \hbox{Tr} \left( \rho \log {\rho} \right),$

where the logarithm is again taken in base 2. In general, to calculate $\; \log \rho$ , one would use the Borel functional calculus. If ρ acts on a finite dimensional Hilbert space and has eigenvalues $\lambda_1, \cdots, \lambda_n$ , then we recover the Shannon entropy:

$S(\rho) = - \hbox{Tr} \left( \rho \log {\rho} \right) = - \sum_i \lambda_i \log \lambda_i$ .

Since an event of probability 0 should not contribute to the entropy, we adopt the convention that $0 \log 0 \; = 0$ . This extends to the infinite dimensional case as well: if ρ has spectral resolution $\rho = \int \lambda d P_{\lambda}$ , then we assume the same convention when calculating

$\rho \log \rho = \int \lambda \log \lambda d P_{\lambda} .$

As in statistical mechanics, one can say that the more uncertainty (number of microstates) the system should possess, the larger the entropy. For example, the entropy of any pure state is zero, which is unsurprising since there is no uncertainty about a system in a pure state. The entropy of any of the two subsystems of the entangled state discussed above is $log2$ (which can be shown to be the maximum entropy for $2 \times 2$ mixed states).

[edit] As a measure of entanglement

Entropy provides one tool which can be used to quantify entanglement, although other entanglement measures exist.^{[citation needed]} If the overall system is pure, the entropy of one subsystem can be used to measure its degree of entanglement with the other subsystems.

For bipartite pure states, the von Neumann entropy of reduced states is the unique measure of entanglement in the sense that it is the only function on the family of states that satisfies certain axioms required of an entanglement measure.

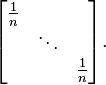
It is a classical result that the Shannon entropy achieves its maximum at, and only at, the uniform probability distribution {1/n,...,1/n}. Therefore, a bipartite pure state

$\rho \in H \otimes H$

is said to be a maximally entangled state if there exists some local bases on H such that the reduced state of ρ is the diagonal matrix

$\begin{bmatrix} \frac{1}{n}& \; & \; \\ \; & \ddots & \; \\ \; & \; & \frac{1}{n}\end{bmatrix}.$

For mixed states, the reduced von Neumann entropy is not the unique entanglement measure.

As an aside, the information-theoretic definition is closely related to entropy in the sense of statistical mechanics^{[citation needed]} (comparing the two definitions, we note that, in the present context, it is customary to set the Boltzmann constant $k = 1$ ). For example, by properties of the Borel functional calculus, we see that for any unitary operator U,

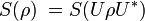$S(\rho) \; = S(U \rho U^*)$ .

Indeed, without the above property, the von Neumann entropy would not be well-defined. In particular, U could be the time evolution operator of the system, i.e.

$U(t) \; = \exp \left(\frac{-i H t }{\hbar}\right)$

where H is the Hamiltonian of the system. This associates the reversibility of a process with its resulting entropy change, i.e. a process is reversible if, and only if, it leaves the entropy of the system invariant. This provides a connection between quantum information theory and thermodynamics.

[edit] Applications of entanglement

Entanglement has many applications in quantum information theory. Mixed state entanglement can be viewed as a resource for quantum communication. With the aid of entanglement, otherwise impossible tasks may be achieved. Among the best known applications of entanglement are superdense coding and quantum state teleportation. Efforts to quantify this resource are often termed entanglement theory.^[4] ^[5] Quantum entanglement also has many different applications in the emerging technologies of quantum computing and quantum cryptography, and has been used to realize quantum teleportation experimentally^[6]. At the same time, it prompts some of the more philosophically oriented discussions concerning quantum theory.^{[citation needed]} The correlations predicted by quantum mechanics, and observed in experiment, reject the principle of local realism, which is that information about the state of a system can only be mediated by interactions in its immediate surroundings and that the state of a system exists and is well-defined before any measurement. Different views of what is actually occurring in the process of quantum entanglement can be related to different interpretations of quantum mechanics. In the previously standard one, the Copenhagen interpretation, quantum mechanics is neither "real" (since measurements do not state, but instead prepare properties of the system) nor "local" (since the state vector $|\psi\rangle$ comprises the simultaneous probability amplitudes for all positions, e.g. $|\psi\rangle \to \psi(x,y,z)$ ); the properties of entanglement are some of the many reasons why the Copenhagen Interpretation is no longer considered standard by a large proportion of the scientific community.

Other uses:

Quantum computers use entanglement and superposition.
The Reeh-Schlieder theorem of quantum field theory is sometimes seen as the QFT analogue of quantum entanglement.

[edit] See also

[edit] References

Specific references:

^ Einstein A, Podolsky B, Rosen N (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Phys. Rev. 47 (10): 777–780. doi:10.1103/PhysRev.47.777.
^ Paulson, Tom (2006-11-15). "Going for a blast in the real past". Seattle Post-Intelligencer. http://seattlepi.nwsource.com/local/292378_timeguy15.html?source=mypi. Retrieved on 2006-12-19.
^ Boyle, Alan (2006-11-21). "Time-travel physics seems stranger than fiction". MSNBC. http://www.msnbc.msn.com/id/15817394/. Retrieved on 2006-12-19.
^ Entanglement Theory Tutorials from Imperial College London
^ M.B. Plenio and S. Virmani, An introduction to entanglement measures, Quant. Inf. Comp. 7, 1 (2007) [1]
^ Dik Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred Eibl, Harald Weinfurter & Anton Zeilinger, Experimental Quantum Teleportation, Nature vol.390, 11 Dec 1997, pp.575. (Summarized at http://www.quantum.univie.ac.at/research/photonentangle/teleport/)

General references:

Horodecki M, Horodecki P, Horodecki R (1996). "Separability of mixed states: necessary and sufficient conditions". Physics Letters A: 210.
Gurvits L (2003). "Classical deterministic complexity of Edmonds' Problem and quantum entanglement". Proceedings of the thirty-fifth annual ACM symposium on Theory of computing: 10. doi:10.1145/780542.780545.
Bengtsson I, Zyczkowski K (2006). "Geometry of Quantum States". An Introduction to Quantum Entanglement. Cambridge: Cambridge University Press.
Steward EG (2008-03-24). Quantum Mechanics: Its Early Development and the Road to Entanglement. Imperial College Press. ISBN 978-1860949784.
Horodecki R, Horodecki P, Horodecki M, Horodecki K (2007). "Quantum entanglement". Rev. Mod. Phys.. http://arxiv.org/abs/quant-ph/0702225.
Plenio MB, Virmani S (2007). "An introduction to entanglement measures". Quant. Inf. Comp. 7, 1 (2007). http://arxiv.org/abs/quant-ph/0504163.

[edit] External links

[Einstein1935-0] Einstein A, Podolsky B, Rosen N (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?". Phys. Rev. 47 (10): 777–780. doi:10.1103/PhysRev.47.777.

[1] Paulson, Tom (2006-11-15). "Going for a blast in the real past". Seattle Post-Intelligencer. http://seattlepi.nwsource.com/local/292378_timeguy15.html?source=mypi. Retrieved on 2006-12-19.

[2] Boyle, Alan (2006-11-21). "Time-travel physics seems stranger than fiction". MSNBC. http://www.msnbc.msn.com/id/15817394/. Retrieved on 2006-12-19.

[3] Entanglement Theory Tutorials from Imperial College London

[4] M.B. Plenio and S. Virmani, An introduction to entanglement measures, Quant. Inf. Comp. 7, 1 (2007) [1]

[5] Dik Bouwmeester, Jian-Wei Pan, Klaus Mattle, Manfred Eibl, Harald Weinfurter & Anton Zeilinger, Experimental Quantum Teleportation, Nature vol.390, 11 Dec 1997, pp.575. (Summarized at http://www.quantum.univie.ac.at/research/photonentangle/teleport/)

[1]

[2]

[3]

[4]

[5]

[6]

Quantum entanglement

From Wikipedia, the free encyclopedia

Contents

[edit] Background

[edit] Pure states

[edit] Ensembles

[edit] Reduced density matrices

[edit] Entropy

[edit] Definition

[edit] As a measure of entanglement

[edit] Applications of entanglement

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages