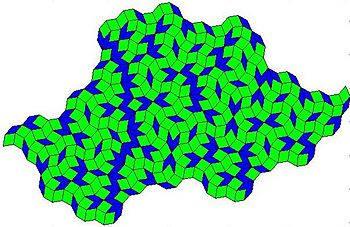
Penrose tiling
From Wikipedia, the free encyclopedia
A Penrose tiling is a nonperiodic tiling generated by an aperiodic set of prototiles named after Roger Penrose, who investigated these sets in the 1970s. Because all tilings obtained with the Penrose tiles are non-periodic, Penrose tilings are considered aperiodic tilings.[1] Among the infinitely many possible tilings there are two that possess both mirror symmetry and fivefold rotational symmetry, as in the diagram at the right, and the term Penrose tiling usually refers to them.
A Penrose tiling has many remarkable properties, most notably:
- It is nonperiodic, which means that it lacks any translational symmetry. More informally, a shifted copy will never match the original exactly.
- Any finite region in a tiling appears infinitely many times in that tiling and, in fact, in any other tiling. This property would be trivially true of a tiling with translational symmetry but is non-trivial when applied to the non-periodic Penrose tilings.
- It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction; the diffractogram reveals both the underlying fivefold symmetry and the long range order. This order reflects the fact that the tilings are organized, not through translational symmetry, but rather through a process sometimes called "deflation" or "inflation."
Robert Ammann independently discovered the tiling at approximately the same time as Penrose.
Various methods to construct the tilings have been proposed: matching rules, substitutions, cut and project schemes and covering.
Contents |
[edit] Historical background
The sets of tiles proposed by Penrose are among the most simple examples of a counter-intuitive mathematical fact - the existence of aperiodic sets. In 1961, Hao Wang noted connections between problems in geometry—specifically problems about tiling—and a certain class of decision problem.[2] As an aside, he observed that if the so-called Domino Problem were undecidable, then there would have to exist an aperiodic set of tiles. As the existence of such a set seemed implausible, Wang conjectured no such set could exist, and that the Domino Problem is decidable for tiles in the plane.
In his 1964 thesis, Robert Berger disproved Wang's conjecture, proving that the Domino Problem is in fact undecidable, and producing an aperiodic set of 104 distinct tiles. (In his published monograph,[3] Berger gives only a larger set of 20426 tiles.)
This number was further reduced by Donald Knuth, Hans Läuchli and then Raphael Robinson, who gave an aperiodic set of just six tiles (and simplified Berger's proof) in an elegant 1971 paper.[4] In 1972, Roger Penrose gave the first of several variations of tiles forcing a hierarchical pentagonal structure, a set of six tiles. Over the next several years, other variations were found, with the participation of Raphael Robinson, Robert Ammann and John H. Conway.
In 1981 De Bruijn explained a method to construct Penrose tilings[5] from five families of parallel lines as well as a "cut and project method", in which Penrose tilings are obtained as two-dimensional projections from a five-dimensional cubic structure. In this approach the Penrose tiling is considered as a set of points, its vertices, while its tiles are just the geometrical shapes defined by connecting edges.
[edit] The original Penrose tiling (P1)
The original Penrose tiling was proposed in 1974 in a paper entitled the Role of aesthetics in pure and applied research.[6] Not more than one fifth of the paper deals with it but Penrose admits that the tiling was its real point. Later Penrose acknowledged inspiration from the work of Johannes Kepler. In his book Harmonices Mundi Kepler explored tilings built around pentagons and it was shown that his construction can be extended into a Penrose tiling.[7] Earlier traces of this idea have been traced to Dürer's work.
Attempting to tile the plane with regular pentagons must necessarily leave gaps. Penrose found a particular tiling in which the gaps may be filled with three other shapes: a star, a boat and a diamond, as shown on the left. In addition to the tiles, Penrose stated rules, usually called matching rules, that specify how tiles must be attached to one another; these rules are needed to ensure that the tilings are nonperiodic. As there are three distinct sets of matching rules for pentagonal tiles, it is common to consider the set as having three different pentagonal tiles, shown in different colors in the illustration. This leads to a set of six tiles: a thin rhombus or 'diamond', a five pointed star, a 'boat' (roughly 3/5 of a star) and three pentagons.
Penrose later found two more sets of aperiodic tiles, one consisting of tiles known as a 'kite' and a 'dart' (P2) and a second set consisting of two rhombuses (P3). The translation between a P1 tiling and its corresponding P3 tiling is illustrated to the right.
[edit] Rhombus tiling (P3)
The Penrose rhombuses are a pair of rhombuses with equal sides but different angles.
- The thin rhombus t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhombus may be bisected along its short diagonal to form a pair of acute Robinson triangles.
- The thick rhombus T has angles of 72, 108, 72, and 108 degrees. The T rhombus may be bisected along its long diagonal to form a pair of obtuse Robinson triangles.
There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only 7 of these combinations to appear. Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled. The simplest rule, prohibiting two tiles to be put together to form a single parallelogram, is insufficient to ensure aperiodicity.[8] Instead, rules are made that distinguish sides of the tiles and require that only particular sides can be put together with each other. An example of appropriate matching rules is shown in the upper part of the diagram to the left. Tiles must be assembled so that the curves across their edges match in color and position. An equivalent condition is that tiles must be assembled so that the bumps on their edges fit together. The same rules can be specified with other formulations.
There are arbitrarily large finite patches with tenfold symmetry and at most one center point of global tenfold symmetry where ten mirror lines cross. As the tiling is aperiodic, there is no translational symmetry—the pattern cannot be shifted to match itself over the entire plane. However, any bounded region, no matter how large, will be repeated an infinite number of times within the tiling. Therefore a finite patch cannot differentiate between the uncountably many Penrose tilings, nor even determine which position within the tiling is being shown. The only way to distinguish the two symmetric Penrose tilings from the others is that their symmetry continues to infinity.
The rhombuses may be cut in half to form a pair of triangles, called Robinson triangles, which can be used to produce the Penrose tilings as a substitution tiling. The Robinson triangles are the isosceles 36º-36º-108º and 72º-72º-36º triangles. Each of these triangles has edges in the ratio of 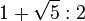 , the golden ratio. The rules that enforce aperiodicity on a Robinson triangle tiling make the triangles asymmetric, and each triangle appears in conjunction with its mirror image to form a rhombus, kite, or dart.
, the golden ratio. The rules that enforce aperiodicity on a Robinson triangle tiling make the triangles asymmetric, and each triangle appears in conjunction with its mirror image to form a rhombus, kite, or dart.
[edit] Drawing the Penrose tiling P3
The rhombus Penrose tiling can be drawn using the following L-system:
variables: 1 6 7 8 9 [ ] constants: + − start: [7]++[7]++[7]++[7]++[7] rules: 6 → 81++91−−−−71[−81−−−−61]++ 7 → +81−−91[−−−61−−71]+ 8 → −61++71[+++81++91]− 9 → −−81++++61[+91++++71]−−71 1 → (eliminated at each iteration) angle: 36º
Here 1 means "draw forward", + means "turn left by angle", and − means "turn right by angle" (see turtle graphics). The [ means save the present position and direction to restore them when corresponding ] is executed. The symbols 6, 7, 8 and 9 do not correspond to any action; they are there only to produce the correct curve evolution.
[edit] Kite and Dart tiling (P2)
The quadrilaterals called the 'Kite' and 'Dart' can also be used to form a Penrose tiling.
- The Kite is a quadrilateral whose four corners have angles of 72, 72, 72, and 144 degrees. The Kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles.
- The Dart is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The Dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles.
The green and the red arcs in the tiles constrain the placement of tiles: When two tiles share an edge in a tiling, the patterns must match at these edges. For example, the concave vertex of a Dart cannot be filled with a single Kite, but must be filled with a pair of Kites.
[edit] Deflation
A substitution method known as deflation, the steps of which are described below, will produce a kite and dart Penrose tiling. Starting with a finite tiling called the axiom, deflation proceeds with a sequence of steps called generations. The axiom can be as simple as a single tile. In one generation of deflation, each tile is replaced with one or more new tiles that exactly cover the area of the original tile. The new tiles are scaled-down versions of the original tiles. The substitution rules guarantee that the new tiles are arranged according to the matching rules.
Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles. Given sufficiently many generations, the tiling will contain a scaled-down version of the axiom that does not touch the boundary of the tiling. The axiom can then be surrounded by full-size tiles corresponding to tiles that appear in the scaled-down version. This extended tiling can be used as a new axiom, producing larger and larger extended tilings and ultimately covers the entire plane.
[edit] An example: three generations of four axioms
This is an example of successive generations of deflation starting from different axioms. In the case of the 'Sun' and 'Star', the scaled-down interior version of the axiom appears in generation 2. The 'Sun' also appears in the interior of its generation 3.
| Name | Generation 0 (or axiom) | Generation 1 | Generation 2 | Generation 3 |
|---|---|---|---|---|
| Kite (half) |  |
 |
 |
 |
| Dart (half) |  |
 |
 |
 |
| Sun |  |
 |
 |
 |
| Star |  |
 |
 |
 |
[edit] Decagonal covering
In 1996 German mathematician Petra Gummelt demonstrated that a covering equivalent to the Penrose tiling can be built by covering the plane with a single decagonal tile[9] if two kinds of overlap are allowed. This novel approach is called 'covering' to distinguish it from non-overlapping 'tiling'. The decagonal tile is decorated with colored patches and the covering rule allows only the overlap of these decorations.
Decomposing the decagonal tile into kites and darts transform the aperiodic covering into a Penrose tiling. If a fat 'T' rhombus is inscribed into each decagon, that part of the Penrose tiling corresponding to these shapes is obtained, while places for thin tiles are left unoccupied.
The covering method is taken to be a realistic model for the growth of quasicrystals. Different atomic clusters 'share' the fragments from which the aperiodic structure is built. The analogy with crystals constructed from a unit cell is restored when the overlapping decagons are seen as quasi-unit cells.
[edit] Fibonacci and golden ratio features
The Penrose tiling, the Fibonacci sequence and the golden ratio are intricately related and perhaps they should be considered as different aspects of the same phenomenon.
- The ratio of thick T to thin t rhombuses in the infinite tile is the golden ratio
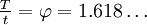
- The Conway worms, sequences of neighbouring rhombuses with parallel sides, are Fibonacci ordered appearances of T and t and thus the Ammann bars also form Fibonacci ordered grids
- around each 5T − star a segmented Fibonacci spiral is formed by the sides of rhombuses.[10]
- The distances between repeated finite motifs in the tiling grow as Fibonacci numbers when the size of the motif increases
- the distribution of oscillation frequencies in a Penrose tiling shows bands and gaps whose widths are in proportions expressed by φ.[11]
- The substitution scheme
 introduces φ as a scaling factor; its matrix is the square of the Fibonacci substitution matrix; implemented as a symbol sequence (e.g. 1→101, 0→10) this substitution produces a series of words with lengths which are the Fibonacci numbers with odd index, F(2n + 1) for n = 1,2,3..., the limit being the infinite Fibonacci binary sequence.
introduces φ as a scaling factor; its matrix is the square of the Fibonacci substitution matrix; implemented as a symbol sequence (e.g. 1→101, 0→10) this substitution produces a series of words with lengths which are the Fibonacci numbers with odd index, F(2n + 1) for n = 1,2,3..., the limit being the infinite Fibonacci binary sequence. - The eigenvalues of the substitution matrix are φ+1 (=φ²) and 2-φ (=1/φ²).
[edit] Related tilings and topics
The three variants of the Penrose tiling are equivalent in the sense of being mutually locally derivable but other possibilities, including related nonequivalent tilings, exist. For instance if the matching rules for the rhombus tiling are simplified as those for the kite and dart, a binary tiling[12] is obtained. Its underlying symmetry is also fivefold but it is not a quasicrystal. It can be obtained either by 'decorating' the rhombuses of the original tiling with smaller ones or directly by the substitutions  ,
,  , but not by de Bruijn's cut-and-project method.[13] The hexagon-boat-star and Mikulla-Roth tilings are two other closely related variants.
, but not by de Bruijn's cut-and-project method.[13] The hexagon-boat-star and Mikulla-Roth tilings are two other closely related variants.
The aesthetic value of unusual tilings has always been appreciated and remains an abiding source of interest in them. The formal defining properties of Penrose tilings are typically disregarded when used in art, as only the visual similarity is noted. The similarity with some decorative patterns used in the Middle East has been frequently observed[14][15] and in a paper by Lu and Steinhardt offered evidence that a Penrose tiling underlies some examples of medieval Islamic art.[16]
Drop City artist Clark Richert used Penrose rhombuses in artwork in 1970. Art historian Martin Kemp has observed that Albrecht Dürer has sketched similar motifs of a rhombus tiling.[17]
[edit] See also
[edit] Notes
- ^ Aaron Zerhusen (August 1997). "Quasicrystals and Aperiodic Tilings". http://www.ms.uky.edu/~lee/zerhusen/quasi.html. Retrieved on 2008-12-17.
- ^ H. Wang, Proving theorems by pattern recognition II, Bell Systems Tech. J. 40 (1961), 1-42.
- ^ R. Berger, The undecidability of the domino problem, Memoirs Amer. Math. Soc. 66, (1966)
- ^ R.M. Robinson, Undecidability and nonperiodicity of tilings in the plane, Inv. Math 12 (1971), 177-190.
- ^ N. G. de Bruijn (1981). "Algebraic theory of Penrose's nonperiodic tilings of the plane, I, II" (PDF). Indagationes mathematicae Vol. 43 (No. 1): 39–66. http://alexandria.tue.nl/repository/freearticles/597566.pdf.
- ^ Penrose R., Bull. Inst. Maths. Appl. 10 (1974) 266
- ^ Luck R., Dürer-Kepler-Penrose: the development of pentagonal tilings, Mat. Sci. Eng. 294-6 (2000) 263-7
- ^ Statements to the contrary appear are widely published; a counterexample is Image:PenroseBogus.GIF
- ^ P. Gummelt, Geometriae Dedicata 62, 1 (1996)
- ^ "Fivefold and Spiral Symmetry Associated with Fibonacci Sequence". http://www.geocities.com/capecanaveral/lab/5833/chaos25.html. Retrieved on 2008-12-17.
- ^ Maynard J.D., Rev. Mod. Phys. 73(2001)401
- ^ Frédéric Lançon and Luc Billard (1988). "Two-dimensional system with a quasi-crystalline ground state". Journal de Physique 49: 249–256. doi:., also described at [1]
- ^ C. Godrèche and F. Lançon (1992). "A simple example of a non-Pisot tiling with five-fold symmetry". Journal de Physique I 2: 207–220. doi:. http://www.edpsciences.org/10.1051/jp1:1992134., also described at [2]
- ^ Zaslavskiy G. et al (1988). "Minimal chaos, stochastic web and structures with 'quasicrystal' type symmetry (in Russian)". Uspekhi Fizicheskih Nauk 156 ((oct.)10): 193–251. http://ufn.ioc.ac.ru/ufn88/ufn88_10/Russian/r8810a.pdf.
- ^ E. Makovicky (1992), 800-year-old pentagonal tiling from Maragha, Iran, and the new varieties of aperiodic tiling it inspired. In: I. Hargittai, editor: Fivefold Symmetry, pp.67-86. World Scientific, Singapore-London
- ^ Peter J. Lu and Paul J. Steinhardt (2007). "Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture". Science 315: 1106–1110. doi:. PMID 17322056. http://www.physics.harvard.edu/~plu/publications/Science_315_1106_2007.pdf.
- ^ Kemp, Martin (2005). "Science in culture: A trick of the tiles". Nature 436: 332. doi:.
[edit] References
- Penrose, Roger. (1989) The Emperor's New Mind. ISBN 0-19-851973-7
- Gardner, Martin. "Penrose Tiles", chapter 7 in his book The Colossal Book of Mathematics. ISBN 0-393-02023-1
[edit] External links
| Wikimedia Commons has media related to: Penrose tiles |
- A wealth of information on the Penrose tiling is available on the Internet. Two sites among the best are: John Savard's pages on Pentagonal Tiling and Eric Hwang's Penrose Tiling
- The Penrose tiling on the Tilings Encylcopedia
- An implementation of the aforementioned L-System (Blog entry / SVG file) as a Scalable Vector Graphic with ECMAScript by Sam Ruby
- QuasiTiler: Explanation of why the Penrose tiling is a projection of 5-dimensional cubes onto a 2-dimensional plane (as shown by Nicolaas Govert de Bruijn in 1981)
- American Mathematical Society article excellently explaining inflation and why the Penrose tiling must be aperiodic
- Two theories for the formation of quasicrystals resembling Penrose tilings
- On de Bruijn Grids and Tilings at MathPages
- Penrose tiles used in Architecture by William Chow.
- The Geometry Junkyard: Penrose Tiling by David Eppstein.