ISO 216

From Wikipedia, the free encyclopedia

**ISO 269 sizes**
(mm × mm)
C Series
C0	917 × 1297
C1	648 × 917
C2	458 × 648
C3	324 × 458
C4	229 × 324
C5	162 × 229
C6	114 × 162
C7/6	81 × 162
C7	81 × 114
C8	57 × 81
C9	40 × 57
C10	28 × 40
DL	110 × 220

**ISO 216 sizes**
(mm × mm)
B Series
B0	1000 × 1414
B1	707 × 1000
B2	500 × 707
B3	353 × 500
B4	250 × 353
B5	176 × 250
B6	125 × 176
B7	88 × 125
B8	62 × 88
B9	44 × 62
B10	31 × 44

**ISO 216 sizes**
(mm × mm)
A Series
A0	841 × 1189
A1	594 × 841
A2	420 × 594
A3	297 × 420
A4	210 × 297
A5	148 × 210
A6	105 × 148
A7	74 × 105
A8	52 × 74
A9	37 × 52
A10	26 × 37

ISO 216 specifies international standard (ISO) paper sizes used in most countries in the world today. It is the standard which defines the commonly available A4 paper size. The underlying principle is that when rectangles with width/length ratio 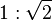$1:\sqrt{2}$ are cut or folded in half the rectangles thus formed retain the original width/length ratio.

[edit] History

The international ISO standard is based on the German DIN standard 476 (DIN 476) from 1922.

Some of the formats contained therein were independently invented in France during its revolution, but were later forgotten.^[1]

The aspect ratio used by this standard was mentioned in a letter by the German Georg Christoph Lichtenberg, written on 25 October 1786.^[2]

ISO 216:1975, defines two series of paper sizes: A and B
ISO 269:1985, defines a C series for envelopes
ISO 217:1995, defines two untrimmed series of raw paper sizes: RA and SRA

[edit] A series

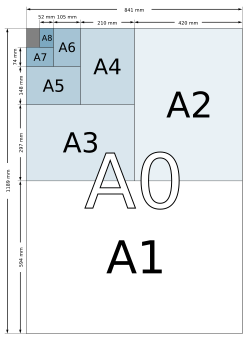
A size chart illustrating the ISO A series.

Paper in the A series format has a 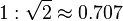$1:\sqrt{2} \approx 0.707$ aspect ratio, although this is rounded to the nearest millimetre. A0 is defined so that it has an area of 1 m², prior to the above mentioned rounding. Successive paper sizes in the series (A1, A2, A3, etc.) are defined by halving the preceding paper size, cutting parallel to its shorter side (so that the long side of A(n+1) is the same length as the short side of An, again prior to rounding).

The most frequently used of this series is the size A4 (210 × 297 mm). A4 paper is 6 mm narrower and 18 mm longer than the "Letter" paper size, 8½ × 11 inches (216 × 279 mm), commonly used in North America.

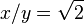The geometric rationale behind the square root of 2 is to maintain the aspect ratio of each subsequent rectangle after cutting the sheet in half, perpendicular to the larger side. Given a rectangle with a longer side, x, and a shorter side, y, the following equation shows how the aspect ratio of a rectangle compares to that of a half rectangle: $\ x/y = y/(x/2)$ which reduces to $x/y = \sqrt{2}$ or an aspect ratio of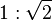 $1 : \sqrt{2}$

The formula that gives the larger border of the paper size A $n$ in metres and without rounding off is the geometric sequence: $a n = 2 1 / 4 - n / 2$ . The paper size A $n$ thus has the dimension $a n$ × $a n + 1$ .

The exact millimetre measurement of the long side of A $n$ is given by 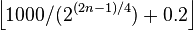$\left \lfloor 1000/(2^{(2n-1)/4})+0.2 \right \rfloor$ .

[edit] B series

A size chart illustrating the ISO B series.

The B series formats are geometric means between the A series format with a particular number and the A series format with one lower number. For example, B1 is the geometric mean between A1 and A0. The sides of B0 are 1 m to $\sqrt{2}$ m.

There is also an incompatible Japanese B series defined by the JIS. The lengths of JIS B series paper are approximately 1.22 times those of A-series paper.

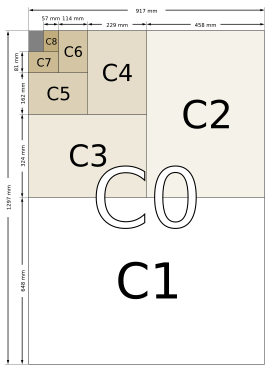
The exact millimetre measurement of the long side of B $n$ is given by $\left \lfloor 1000/(2^{(n-1)/2})+0.2 \right \rfloor$ .

[edit] C series

A size chart illustrating the ISO C series.

The C series formats are geometric means between the B series format with a particular number and the A series format with the same number, (e.g., C2 is the geometric mean between B2 and A2). The C series formats are used mainly for envelopes. An A4 page will fit into a C4 envelope. C series envelopes follow the same ratio principle as the A series pages. For example, if an A4 page is folded in half so that it is A5 in size, it will fit into a C5 envelope (which will be the same size as a C4 envelope folded in half).

A, B, and C paper fit together as part of a geometric progression, with ratio of successive side lengths of 2^1/8, though there is no size half-way between Bn and An+1: A4, C4, B4, D4, A5, ...; there is such a D-series in the Swedish extensions to the system.

The exact millimetre measurement of the long side of C $n$ is given by 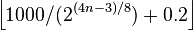$\left \lfloor 1000/(2^{(4n-3)/8})+0.2 \right \rfloor$ .

[edit] Tolerances

The tolerances specified in the standard are:

±1.5 mm for dimensions up to 150 mm,
±2.0 mm for lengths in the range 150 to 600 mm, and
±3.0 mm for any dimension above 600 mm.

[edit] A, B, C comparison

ISO/DIN paper sizes in millimetres and in inches
	A Series Formats		B Series Formats		C Series Formats
size	mm	inches	mm	inches	mm	inches
0	841 × 1189	33.1 × 46.8	1000 × 1414	39.4 × 55.7	917 × 1297	36.1 × 51.1
1	594 × 841	23.4 × 33.1	707 × 1000	27.8 × 39.4	648 × 917	25.5 × 36.1
2	420 × 594	16.5 × 23.4	500 × 707	19.7 × 27.8	458 × 648	18.0 × 25.5
3	297 × 420	11.7 × 16.5	353 × 500	13.9 × 19.7	324 × 458	12.8 × 18.0
4	210 × 297	8.3 × 11.7	250 × 353	9.8 × 13.9	229 × 324	9.0 × 12.8
5	148 × 210	5.8 × 8.3	176 × 250	6.9 × 9.8	162 × 229	6.4 × 9.0
6	105 × 148	4.1 × 5.8	125 × 176	4.9 × 6.9	114 × 162	4.5 × 6.4
7	74 × 105	2.9 × 4.1	88 × 125	3.5 × 4.9	81 × 114	3.2 × 4.5
8	52 × 74	2.0 × 2.9	62 × 88	2.4 × 3.5	57 × 81	2.2 × 3.2
9	37 × 52	1.5 × 2.0	44 × 62	1.7 × 2.4	40 × 57	1.6 × 2.2
10	26 × 37	1.0 × 1.5	31 × 44	1.2 × 1.7	28 × 40	1.1 × 1.6

[edit] Application

Before the adoption of ISO 216, many different paper formats were used internationally. These formats did not fit into a coherent system and were defined in terms of non-metric units.

The ISO 216 formats are organized around the ratio 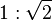$1:\sqrt{2}$ ; two sheets next to each other together have the same ratio, sideways. In scaled photocopying, for example, two A4 sheets in reduced size fit exactly onto one A4 sheet, an A4 sheet in magnified size onto an A3 sheet, and an A5 sheet scaled up onto a A4 sheet, in each case there is neither waste nor want. The principal countries not generally using the ISO paper sizes are the United States and Canada, which use the Letter, Legal and Executive system. (Canada uses a P-series of sizes, which are the US paper sizes rounded to metric dimensions.)

Rectangular sheets of paper with the ratio 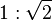$1:\sqrt{2}$ are popular in paper folding, where they are sometimes called "A4 rectangles" or "silver rectangles".^[3] (Confusingly, "silver rectangle" can also refer to a rectangle in the proportion $1:(1+\sqrt{2})$ ), known as the silver ratio.)

[edit] See also

[edit] References

[edit] External links

Wikimedia Commons has media related to: DIN EN ISO 216

International standard paper sizes: ISO 216 details and rationale
ISO 216 at iso.org

[0] "www.cl.cam.ac.uk/~mgk25/loi-timbre.html". http://www.cl.cam.ac.uk/~mgk25/loi-timbre.html.

[1] "www.cl.cam.ac.uk/~mgk25/lichtenberg-letter.html". http://www.cl.cam.ac.uk/~mgk25/lichtenberg-letter.html.

[2] "www.britishorigami.info/academic/lister/a4.htm". http://www.britishorigami.info/academic/lister/a4.htm.

[1]

[2]

[3]

ISO 216

From Wikipedia, the free encyclopedia

Contents

[edit] History

[edit] A series

[edit] B series

[edit] C series

[edit] Tolerances

[edit] A, B, C comparison

[edit] Application

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages