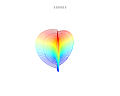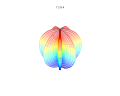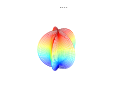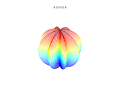Superformula
From Wikipedia, the free encyclopedia
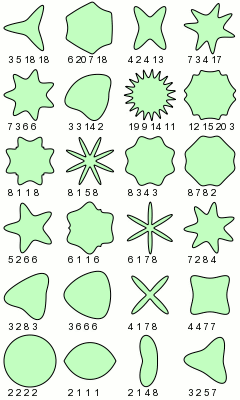
The superformula is a generalization of the superellipse and was first proposed by Johan Gielis.
Gielis suggested that the formula can be used to describe many complex shapes and curves that are found in nature. Others point out that the same can be said about many formulas with a sufficient number of parameters.
In polar coordinates, with r the radius and φ the angle, the superformula is:
![r\left(\phi\right) =
\left[
\left|
\frac{\cos\left(\frac{m\phi}{4}\right)}{a}
\right| ^{n_{2}}
+
\left|
\frac{\sin\left(\frac{m\phi}{4}\right)}{b}
\right| ^{n_{3}}
\right] ^{-\frac{1}{n_{1}}}](http://upload.wikimedia.org/math/9/3/2/932649147ef032f63b06bafbd22d2554.png)
The formula appeared in a work by Gielis. It was obtained generalizing the superellipse, named and popularized by Piet Hein, a Danish mathematician.
Contents |
[edit] Plots
[edit] GNU_Octave program
A GNU_Octave program for generating these figures:
function sf2d(n,a)
u=[0:.001:2*pi];
raux=abs(1/a(1).*abs(cos(n(1)*u/4))).^n(3)+abs(1/a(2).*abs(sin(n(1)*u/4))).^n(4);
r=abs(raux).^(-1/n(2));
x=r.*cos(u);
y=r.*sin(u);
plot(x,y);
endfunction;
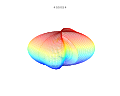
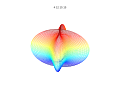
[edit] Extension to higher dimensions
It is possible to extend the formula to 3, 4, or n dimensions, by means of spherical product of superformulas. For example, the 3D parametric surface is obtained multiplying two superformulas S1 and S2. The coordinates are defined by the relations:
where φ varies between -π/2 and π/2 (latitude) and θ between -π and π (longitude).
[edit] Plots
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
 3D superformula: a=b=1; m, n1, n2 and n3 are shown in picture. |
[edit] GNU_Octave program
A GNU_Octave program for generating these figures:
function sf3d(n, a)
u=[-pi:.05:pi];
v=[-pi/2:.05:pi/2];
nu=length(u);
nv=length(v);
for i=1:nu
for j=1:nv
raux1=abs(1/a(1)*abs(cos(n(1).*u(i)/4))).^n(3)+abs(1/a(2)*abs(sin(n(1)*u(i)/4))).^n(4);
r1=abs(raux1).^(-1/n(2));
raux2=abs(1/a(1)*abs(cos(n(1)*v(j)/4))).^n(3)+abs(1/a(2)*abs(sin(n(1)*v(j)/4))).^n(4);
r2=abs(raux2).^(-1/n(2));
x(i,j)=r1*cos(u(i))*r2*cos(v(j));
y(i,j)=r1*sin(u(i))*r2*cos(v(j));
z(i,j)=r2*sin(v(j));
endfor;
endfor;
mesh(x,y,z);
endfunction;
[edit] References
- Gielis, Johan (2003), "A generic geometric transformation that unifies a wide range of natural and abstract shapes", American Journal of Botany 90 (3): 333–338, ISSN 0002-9122, http://www.amjbot.org/cgi/content/abstract/90/3/333
