Physical constant

From Wikipedia, the free encyclopedia

Jump to: navigation, search

A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.

There are many physical constants in science, some of the most widely recognized being the speed of light in vacuum c, the gravitational constant G, Planck's constant h, the electric constant ε0, and the elementary charge e. Physical constants can take many dimensional forms: the speed of light signifies a maximum speed limit of the universe and is expressed dimensionally as length divided by time; while the fine-structure constant α, which characterizes the strength of the electromagnetic interaction, is dimensionless.

Contents

[edit] Dimensionful and dimensionless physical constants

Whereas the values of physical constants do not depend on the unit system used, the numerical values of dimensionful physical constants do depend on the unit used. Therefore, these numerical values (such as 299,792,458 for the constant speed of light c expressed in units of meters per second) are not values that a theory of physics can be expected to predict.

Ratios of like-dimensioned physical constants do not depend on unit systems in this way (the units cancel), so they are pure (dimensionless) numbers whose values a future theory of physics could conceivably hope to predict. Additionally, all equations describing laws of physics can be expressed without dimensional physical constants via a process known as nondimensionalisation, but the dimensionless constants will remain. Thus, theoretical physicists tend to regard these dimensionless quantities as fundamental physical constants.

However, the phrase fundamental physical constant is also used in other ways. For example, the National Institute of Standards and Technology[1] uses it to refer to any universal physical quantity believed to be constant, such as the speed of light, c, and the gravitational constant G.

The fine-structure constant α is probably the best known dimensionless fundamental physical constant. Many attempts have been made to derive its value (currently measured at about 1/137.035999) from theory, but so far none have succeeded. The same holds for the dimensionless ratios of masses of fundamental particles (the most apparent is mp/me, approximately 1836.152673). With the development of quantum chemistry in the 20th century, however, a vast number of previously inexplicable dimensionless physical constants were successfully computed from theory. As such, some theoretical physicists still hope for continued progress in explaining the values of dimensionless physical constants.

It is known that the universe would be very different if these constants took values significantly different from those we observe. For example, a few percent change in the value of the fine structure constant would be enough to eliminate stars like our Sun. This has prompted attempts at anthropic explanations of the dimensionless physical constants.

[edit] How constant are the physical constants?

Beginning with Paul Dirac in 1937, some scientists have speculated that physical constants may actually decrease in proportion to the age of the universe. Scientific experiments have not yet pinpointed any definite evidence that this is the case, although they have placed upper bounds on the maximum possible relative change per year at very small amounts (roughly 10−5 per year for the fine structure constant α and 10−11 for the gravitational constant G).

It is currently disputed[2][3] that any changes in dimensional physical constants such as G, c, ħ, or ε0 are operationally meaningful;[4] however, a sufficient change in a dimensionless constant such as α is generally agreed to be something that would definitely be noticed. If a measurement indicated that a dimensional physical constant had changed, this would be the result or interpretation of a more fundamental dimensionless constant changing, which is the salient metric. From John D. Barrow 2002:

"[An] important lesson we learn from the way that pure numbers like α define the world is what it really means for worlds to be different. The pure number we call the fine structure constant and denote by α is a combination of the electron charge, e, the speed of light, c, and Planck's constant, h. At first we might be tempted to think that a world in which the speed of light was slower would be a different world. But this would be a mistake. If c, h, and e were all changed so that the values they have in metric (or any other) units were different when we looked them up in our tables of physical constants, but the value of α remained the same, this new world would be observationally indistinguishable from our world. The only thing that counts in the definition of worlds are the values of the dimensionless constants of Nature. If all masses were doubled in value you cannot tell because all the pure numbers defined by the ratios of any pair of masses are unchanged."

[edit] Anthropic principle

Some physicists have explored the notion that if the (dimensionless) fundamental physical constants had sufficiently different values, our universe would be so radically different that intelligent life would probably not have emerged, and that our universe therefore seems to be fine-tuned for intelligent life. The Strong anthropic principle states that it must be because these fundamental constants acquired their respective values that there was sufficient order in the Universe and richness in elemental diversity for life to have formed, which subsequently evolved the necessary intelligence toward observing that these constants have taken on the values they have, which then allowed for our privileged perspective from the Weak anthropic principle standpoint.

[edit] Table of universal constants

Quantity Symbol Value Relative Standard Uncertainty
speed of light in vacuum c \, 299 792 458 m·s−1 defined
Newtonian constant of gravitation 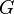G \, 6.67428(67)×10−11 m3·kg−1·s−2 1.0 × 10−4
Planck's constant 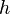h \, 6.626 068 96(33) × 10−34 J·s 5.0 × 10−8
reduced Planck constant 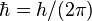\hbar = h / (2 \pi) 3.313 034 48π-1 × 10−34 J·s = 1.054 571 628(53) × 10−34 J·s 5.0 × 10−8

[edit] Table of electromagnetic constants

Quantity Symbol Value[5] (SI units) Relative Standard Uncertainty
magnetic constant (vacuum permeability) 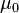\mu_0 \, 4π × 10−7 N·A−2 = 1.256 637 061... × 10−6 N·A−2 defined
electric constant (vacuum permittivity) 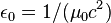\epsilon_0 = 1/(\mu_0 c^2) \, 2.781 625 140 134 046 080 435 224 912 12π-1 × 10-11 F·m−1 = 8.854 187 817... × 10−12 F·m−1 defined
characteristic impedance of vacuum Z_0 = \mu_0 c \, 119.916 983 2π Ω = 376.730 313 461... Ω defined
Coulomb's constant \kappa = 1 / 4\pi\epsilon_0 \, 8.987 551 787 368 176 4 × 109 N·m²·C−2 defined
elementary charge e \, 1.602 176 487(40) × 10−19 C 2.5 × 10−8
Bohr magneton 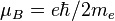\mu_B = e \hbar / 2 m_e 927.400 915(23) × 10−26 J·T−1 2.5 × 10−8
conductance quantum G_0 = 2 e^2 / h \, 7.748 091 717 914 392 775 819 594 884 104 2(53) × 10−5 S 6.8 × 10−10
inverse conductance quantum G_0^{-1} = h / 2 e^2 \, 12 906.403 749 556 760 396 515 369 018 534(88) Ω 6.8 × 10−10
Josephson constant K_J = 2 e / h \, 4.835 978 91(12) × 1014 Hz·V−1 2.5 × 10−8
magnetic flux quantum \phi_0 = h / 2 e \, 2.067 833 667(52) × 10−15 Wb 2.5 × 10−8
nuclear magneton \mu_N = e \hbar / 2 m_p 5.050 783 43(43) × 10−27 J·T−1 8.6 × 10−8
von Klitzing constant R_K = h / e^2 \, 25 812.807 557(18) Ω 6.8 × 10−10

[edit] Table of atomic and nuclear constants

Quantity Symbol Value[5] (SI units) Relative Standard Uncertainty
Bohr radius a_0 = \alpha / 4 \pi R_\infin \, 0.529 177 2108(18) × 10−10 m 3.3 × 10−9
classical electron radius r_e = e^2 / 4\pi\epsilon_0 m_e c^2\, 2.817 940 299 579 513 654 416 052 301 942(58) × 10−15 m 2.1 × 10−9
electron mass m_e \, 9.109 382 15(45) × 10−31 kg 5.0 × 10−8
Fermi coupling constant G_F / (\hbar c)^3 1.166 39(1) × 10−5 GeV−2 8.6 × 10−6
fine-structure constant 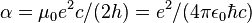\alpha = \mu_0 e^2 c / (2 h) = e^2 / (4 \pi \epsilon_0 \hbar c) \, 7.297 352 5376(50) × 10−3 6.8 × 10−10
Hartree energy E_h = 2 R_\infin h c \, 4.359 744 17(75) × 10−18 J 1.7 × 10−7
proton mass 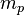m_p \, 1.672 621 637(83) × 10−27 kg 5.0 × 10−8
quantum of circulation h / 2 m_e \, 3.636 947 550(24) × 10−4 m² s−1 6.7 × 10−9
Rydberg constant R_\infin = \alpha^2 m_e c / 2 h \, 10 973 731.568 525(73) m−1 6.6 × 10−12
Thomson cross section (8 \pi / 3)r_e^2 6.652 458 73(13) × 10−29 m² 2.0 × 10−8
weak mixing angle \sin^2 \theta_W = 1 - (m_W / m_Z)^2 \, 0.222 15(76) 3.4 × 10−3

[edit] Table of physico-chemical constants

Quantity Symbol Value[5] (SI units) Relative Standard Uncertainty
atomic mass unit (unified atomic mass unit) m_u = 1 \ u \, 1.660 538 86(28) × 10−27 kg 1.7 × 10−7
Avogadro's number N_A, L \, 6.022 141 5(10) × 1023 mol−1 1.7 × 10−7
Boltzmann constant 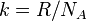k = R / N_A \, 1.380 650 388 238 137 546 253 272 195 613 5(24) × 10−23 J·K−1 1.8 × 10−6
Faraday constant 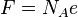F = N_A e \, 96 485.337 716 389 95(83)C·mol−1 8.6 × 10−8
first radiation constant c_1 = 2 \pi h c^2 \, 1.191 042 819 608 808 028 820 490 4π × 10−16 W·m² = 3.741 771 18(19) × 10−16 W·m² 5.0 × 10−8
for spectral radiance c_{1L} \, 1.191 042 82(20) × 10−16 W·m² sr−1 1.7 × 10−7
Loschmidt constant at T=273.15 K and p=101.325 kPa n_0 = N_A / V_m \, 2.686 777 3(47) × 1025 m−3 1.8 × 10−6
gas constant 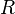R \, 8.314 472(15) J·K−1·mol−1 1.7 × 10−6
molar Planck constant N_A h \, 3.990 312 716(27) × 10−10 J·s·mol−1 6.7 × 10−9
molar volume of an ideal gas at T=273.15 K and p=100 kPa V_m = R T / p \, 2.271 098 026 8(40) × 10−2 m³·mol−1 1.7 × 10−6
at T=273.15 K and p=101.325 kPa 2.241 399 483 641 746 854 182 087 342 709 1(39) × 10−2 m³·mol−1 1.7 × 10−6
Sackur-Tetrode constant at T=1 K and p=100 kPa S_0 / R = \frac{5}{2}
+ \ln\left[ (2\pi m_u k T / h^2)^{3/2} k T / p \right]		 −1.151 704 7(44) 3.8 × 10−6
at T=1 K and p=101.325 kPa −1.164 867 7(44) 3.8 × 10−6
second radiation constant c_2 = h c / k \, 1.438 775 2(25) × 10−2 m·K 1.7 × 10−6
Stefan-Boltzmann constant \sigma = (\pi^2 / 60) k^4 / \hbar^3 c^2 5.670 400(40) × 10−8 W·m−2·K−4 7.0 × 10−6
Wien displacement law constant b = (h c / k) / \, 4.965 114 231... 2.897 768 5(51) × 10−3 m·K 1.7 × 10−6

[edit] Table of adopted values

Quantity Symbol Value (SI units) Relative Standard Uncertainty
conventional value of Josephson constant[6] K_{J-90} \, 4.835 979 × 1014 Hz·V−1 defined
conventional value of von Klitzing constant[7] R_{K-90} \, 25 812.807 Ω defined
molar mass constant M_u = M(\,^{12}\mbox{C}) / 12 1 × 10−3 kg·mol−1 defined
of carbon-12 M(\,^{12}\mbox{C}) = N_A m(\,^{12}\mbox{C}) 1.2 × 10−2 kg·mol−1 defined
standard acceleration of gravity (gee, free-fall on Earth) g_n \,\! 9.806 65 m·s−2 defined
standard atmosphere \mbox{atm} \, 101 325 Pa defined

[edit] Notes

  1. ^ Latest (2006) Values of the Constants; NIST, 2006.
  2. ^ Duff, Michael J. "Comment on time-variation of fundamental constants." High Energy Physics - Theory, 2004.
  3. ^ Duff, M. J.; Okun, L. B.; Veneziano, G. "Trialogue on the number of fundamental constants." Classical Physics, 2002.
  4. ^ c, and ε0 now are defined numerical values, independent of experiment, so observations now are trained elsewhere, for example, upon a changing value of the meter.
  5. ^ a b c The values are given in the so-called concise form; the number in brackets is the standard uncertainty, which is the value multiplied by the relative standard uncertainty.
  6. ^ This is the value adopted internationally for realizing representations of the volt using the Josephson effect.
  7. ^ This is the value adopted internationally for realizing representations of the ohm using the quantum Hall effect.

[edit] References

Retrieved from "http://en.wikipedia.org/wiki/Physical_constant"
Personal tools