Girih tiles
From Wikipedia, the free encyclopedia
Girih tiles are a set of five tiles that were used in the creation of tiling patterns for decoration of buildings in Islamic architecture. They are known to have been used since about the year 1200 and their arrangements found significant improvement starting with the Darb-i Imam shrine in Isfahan in Iran built in 1453.
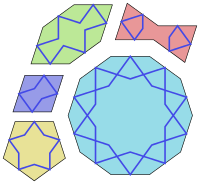
The five shapes of the tiles are:
- a regular decagon with ten interior angles of 144°;
- an elongated (irregular convex) hexagon with interior angles of 72°, 144°, 144°, 72°, 144°, 144°;
- a bow tie (non-convex hexagon) with interior angles of 72°, 72°, 216°, 72°, 72°, 216°;
- a rhombus with interior angles of 72°, 108°, 72°, 108°; and
- a regular pentagon with five interior angles of 108°.
All sides of these figures have the same length; and all their angles are multiples of 36° (π/5). All of them, except the pentagon, have bilateral (reflection) symmetry through two perpendicular lines. Some have additional symmetries. Specifically, the decagon has tenfold rotational symmetry (rotation by 36°); and the pentagon has fivefold rotational symmetry (rotation by 72°).
Girih are lines (strapwork) which decorate the tiles. In most cases, only the girih (and other minor decorations like flowers) are visible rather than the boundaries of the tiles themselves. The girih are piece-wise straight lines which cross the boundaries of the tiles at the center of an edge at 54° (3π/10) to the edge. Two intersecting girih cross each edge of a tile. Most tiles have a unique pattern of girih inside the tile which are continuous and follow the symmetry of the tile. However, the decagon has two possible girih patterns one of which has only fivefold rather than tenfold rotational symmetry.
Contents |
[edit] Periodic or aperiodic?
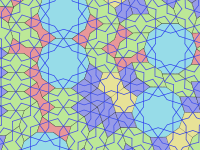
Most uses of girih tiles in Islamic architecture were periodic; they had unit cells which were repeated in the same orientation within a lattice. Some had patterns which could not be extended to a tiling of the entire plane. None of them are known to have had patterns which could be extended to the entire plane only in an aperiodic way.
However, on some buildings, the large girih tiles were decorated with patterns which formed small girih tiles. And on one of these, Darb-i Imam, the subdivision into smaller tiles was done in a way that could have been generalized to an aperiodic tiling of the plane.
[edit] Mathematics of girih tilings
In 2007, Peter J. Lu of Harvard University and Professor Paul J. Steinhardt of Princeton University published a paper in the journal Science suggesting that girih tilings possessed properties consistent with self-similar fractal quasicrystalline tilings such as Penrose tilings (presentation 1974, predecessor works starting in about 1964) predating them by five centuries.[1][2]
This finding was supported both by analysis of patterns on surviving structures, and by examination of 15th century Persian scrolls. If correct, it would indicate that Islamic architects came close to discovering aperiodic tilings some five hundred years before they were discovered by Western mathematicians. However, we have no indication of how much more the architects may have known about the mathematics involved.
[edit] See also
[edit] References
- ^ Peter J. Lu and Paul J. Steinhardt (2007). "Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture". Science 315: 1106–1110. doi:. http://www.physics.harvard.edu/~plu/publications/Science_315_1106_2007.pdf.
- ^ Supplemental figures [1]
[edit] External links
- John Savard's reconstructions
- "Medieval Islamic architecture presages 20th century mathematics". Harvard University Gazette. 2007-02-22. http://www.news.harvard.edu/gazette/2007/03.01/99-tiles.html. Retrieved on 2007-03-14.
- "Medieval Islamic tiling reveals mathematical savvy". New Scientist. 2007-02-22. http://www.newscientist.com/article/dn11235-medieval-islamic-tiling-reveals-mathematical-savvy.html. Retrieved on 2007-03-14.