Statistical classification

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Statistical classification is a procedure in which individual items are placed into groups based on quantitative information on one or more characteristics inherent in the items (referred to as traits, variables, characters, etc) and based on a training set of previously labeled items.

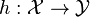Formally, the problem can be stated as follows: given training data \{(\mathbf{x_1},y_1),\dots,(\mathbf{x_n}, y_n)\} produce a classifier h:\mathcal{X}\rightarrow\mathcal{Y} which maps any object 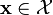\mathbf{x} \in \mathcal{X} to its true classification label y \in \mathcal{Y} defined by some unknown mapping g:\mathcal{X}\rightarrow\mathcal{Y} (ground truth). For example, if the problem is filtering spam, then \mathbf{x_i} is some representation of an email and y is either "Spam" or "Non-Spam".

Statistical classification algorithms are typically used in pattern recognition systems.

Note: in community ecology, the term "classification" is synonymous with what is commonly known (in machine learning) as clustering. See that article for more information about purely unsupervised techniques.

  • The second problem is to consider classification as an estimation problem, where the goal is to estimate a function of the form
P({\rm class}|{\vec x}) = f\left(\vec x;\vec \theta\right)

where the feature vector input is 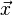\vec x, and the function f is typically parameterized by some parameters \vec \theta. In the Bayesian approach to this problem, instead of choosing a single parameter vector \vec \theta, the result is integrated over all possible thetas, with the thetas weighted by how likely they are given the training data D:

P({\rm class}|{\vec x}) = \int f\left(\vec x;\vec \theta\right)P(\vec \theta|D) d\vec \theta

Examples of classification algorithms include:

An intriguing problem in pattern recognition yet to be solved is the relationship between the problem to be solved (data to be classified) and the performance of various pattern recognition algorithms (classifiers). Van der Walt and Barnard (see reference section) investigated very specific artificial data sets to determine conditions under which certain classifiers perform better and worse than others.

Classifier performance depends greatly on the characteristics of the data to be classified. There is no single classifier that works best on all given problems (a phenomenon that may be explained by the No-free-lunch theorem). Various empirical tests have been performed to compare classifier performance and to find the characteristics of data that determine classifier performance. Determining a suitable classifier for a given problem is however still more an art than a science.

The most widely used classifiers are the Neural Network (Multi-layer Perceptron), Support Vector Machines, k-Nearest Neighbours, Gaussian Mixture Model, Gaussian, Naive Bayes, Decision Tree and RBF classifiers.

Contents

[edit] Evaluation

The measures Precision and Recall are popular metrics used to evaluate the quality of a classification system. More recently, Receiver Operating Characteristic (ROC) curves have been used to evaluate the tradeoff between true- and false-positive rates of classification algorithms.

[edit] Application domains

[edit] References

[edit] External links

[edit] See also

Retrieved from "http://en.wikipedia.org/wiki/Statistical_classification"
Personal tools