Geometric algebra

From Wikipedia, the free encyclopedia

This article is about Clifford algebras of the type Cℓ_{p, q}(R). For other uses, see Geometric algebra (disambiguation).

In mathematical physics, a geometric algebra is a multilinear algebra described technically as a Clifford algebra over a real vector space equipped with a non-degenerate quadratic form. Informally, a geometric algebra is a Clifford algebra that includes a geometric product. This allows the theory and properties of the algebra to be built up in an intuitive, geometric way. The term is also used in a more general sense to describe the study and application of these algebras: so Geometric algebra is the study of geometric algebras.

Geometric algebra is useful in physics problems that involve rotations, phases or imaginary numbers. Proponents of geometric algebra argue it provides a more compact and intuitive description of classical and quantum mechanics, electromagnetic theory and relativity. Current applications of geometric algebra include computer vision, biomechanics and robotics, and spaceflight dynamics.

[edit] The geometric product

A geometric algebra $\mathcal G_n(\mathcal V_n)$ is an algebra constructed over a vector space $\mathcal V_n$ in which a geometric product is defined. The elements of geometric algebra are multivectors. The original vector space $\mathcal V$ is constructed over the real numbers as scalars. From now on, a vector is something in $\mathcal V$ itself. Vectors will be represented by boldface, small case letters (e.g. 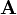$\mathbf a$ ), and multivectors by boldface, upper case letters (e.g. $\mathbf{A}$ ).

The geometric product has the following properties, for all multivectors $\mathbf{A}, \mathbf{B}, \mathbf{C}$ :

Closure
Distributivity over the addition of multivectors:
- $\mathbf{A}(\mathbf{B} + \mathbf{C}) = \mathbf{A}\mathbf{B} + \mathbf{A}\mathbf{C}$
- $(\mathbf{A} + \mathbf{B})\mathbf{C} = \mathbf{A}\mathbf{C} + \mathbf{B}\mathbf{C}$
Associativity
Unit (scalar) element:
- $1 \, \mathbf A = \mathbf A$
Tensor contraction: for any "vector" (a grade-one element) $\mathbf{a}, \mathbf{a}^2$ is a scalar (real number)
Commutativity of the product by a scalar:
- $\lambda \mathbf A = \mathbf A \lambda$

Properties (1) and (2) are among those needed for an algebra over a field. (3) and (4) mean that a geometric algebra is an associative, unital algebra.

The distinctive point of this formulation is the natural correspondence between geometric entities and the elements of the associative algebra. This comes from the fact that the geometric product is defined in terms of the dot product and the wedge product of vectors as

$\mathbf a \, \mathbf b = \mathbf a \cdot \mathbf b + \mathbf a \wedge \mathbf b$

The definition and the associativity of geometric product entails the concept of the inverse of a vector (or division by vector). Thus, one can easily set and solve vector algebra equations that otherwise would be cumbersome to handle. In addition, one gains a geometric meaning that would be difficult to retrieve, for instance, by using matrices. Although not all the elements of the algebra are invertible, the inversion concept can be extended to multivectors. Geometric algebra allows one to deal with subspaces directly, and manipulate them too. Furthermore, geometric algebra is a coordinate-free formalism.

Geometric objects like $\mathbf a \wedge \mathbf b$ are called bivectors. A bivector can be pictured as a plane segment (a parallelogram, a circle etc.) endowed with orientation. One bivector represents all planar segments with the same magnitude and direction, no matter where they are in the space that contains them. However, once either the vector $\mathbf a$ or $\mathbf b$ is meant to depart from some preferred point (e.g. in problems of Physics), the oriented plane $\mathbf B = \mathbf a \wedge \mathbf b$ is determined unambiguously.

The exterior product (or the wedge product; sometimes called the "outer product", although that nomenclature also refers to the tensor product), " $\wedge$ " is defined such that the graded algebra (exterior algebra of Hermann Grassmann) $\wedge^n\mathcal{V}_n$ of multivectors is generated. Multivectors are thus the direct sum of grade k elements (k-vectors), where k ranges from 0 (scalars) to n, the dimension of the original vector space $\mathcal V$ . Multivectors are represented here by boldface caps. Note that scalars and vectors become special cases of multivectors ("0-vectors" and "1-vectors", respectively).

[edit] Comparison with conventional vector algebra

Here are some comparisons between standard ${\mathbb R}^3$ vector relations and their corresponding wedge and geometric product equivalents. All the wedge and geometric product equivalents here are good for more than three dimensions, and some also for two. In two dimensions the cross product is undefined even if what it describes (like torque) is perfectly well defined in a plane without introducing an arbitrary normal vector outside of the space.

Many of these relationships only require the introduction of the wedge product to generalize, but since that may not be familiar to somebody with only a traditional background in vector algebra and calculus, some examples are given.

[edit] Algebraic and geometric properties of cross and wedge products

Cross and wedge products are both antisymmetric:

$\mathbf v \times \mathbf u = - (\mathbf u \times \mathbf v)$

$\mathbf v \wedge \mathbf u = - (\mathbf u \wedge \mathbf v)$

They are both linear in the first operand

$(\mathbf u + \mathbf v) \times \mathbf w = \mathbf u \times \mathbf w + \mathbf v \times \mathbf w$

$(\mathbf u + \mathbf v) \wedge \mathbf w = \mathbf u \wedge \mathbf w + \mathbf v \wedge \mathbf w$

and in the second operand

$\mathbf u \times (\mathbf v + \mathbf w)= \mathbf u \times \mathbf v + \mathbf u \times \mathbf w$

$\mathbf u \wedge (\mathbf v + \mathbf w)= \mathbf u \wedge \mathbf v + \mathbf u \wedge \mathbf w$

In general, the cross product is not associative, while the wedge product is

$(\mathbf u \times \mathbf v) \times \mathbf w \neq \mathbf u \times (\mathbf v \times \mathbf w)$

$(\mathbf u \wedge \mathbf v) \wedge \mathbf w = \mathbf u \wedge (\mathbf v \wedge \mathbf w)$

Both the cross and wedge products of two identical vectors are zero:

$\mathbf u \times \mathbf u = 0$

$\mathbf u \wedge \mathbf u = 0$

$\mathbf u \times \mathbf v$ is perpendicular to the plane containing $\mathbf u$ and $\mathbf v$ .
$\mathbf u \wedge \mathbf v$ is an oriented representation of the same plane.

[edit] Norm of a vector

The norm (length) of a vector is defined in terms of the dot product

${\Vert \mathbf u \Vert}^2 = \mathbf u \cdot \mathbf u$

Using the geometric product this is also true, but this can be also be expressed more compactly as

${\Vert \mathbf u \Vert}^2 = {\mathbf u}^2$

This follows from the definition of the geometric product and the fact that a vector wedge product with itself is zero

$\mathbf u \, \mathbf u = \mathbf u \cdot \mathbf u + \mathbf u \wedge \mathbf u = \mathbf u \cdot \mathbf u$

[edit] Lagrange identity

In three dimensions the product of two vector lengths can be expressed in terms of the dot and cross products

${\Vert \mathbf{u} \Vert}^2 {\Vert \mathbf{v} \Vert}^2 = ({\mathbf{u} \cdot \mathbf{v}})^2 + {\Vert \mathbf{u} \times \mathbf{v} \Vert}^2$

The corresponding generalization expressed using the geometric product is

${\Vert \mathbf{u} \Vert}^2 {\Vert \mathbf{v} \Vert}^2 = ({\mathbf{u} \cdot \mathbf{v}})^2 - (\mathbf{u} \wedge \mathbf{v})^2$

This follows from by expanding the geometric product of a pair of vectors with its reverse

$(\mathbf{u} \mathbf{v})(\mathbf{v} \mathbf{u}) = ({\mathbf{u} \cdot \mathbf{v}} + {\mathbf{u} \wedge \mathbf{v}}) ({\mathbf{u} \cdot \mathbf{v}} - {\mathbf{u} \wedge \mathbf{v}})$

[edit] Determinant expansion of cross and wedge products

$\mathbf u \times \mathbf v = \sum_{i<j}{ \begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix} {\mathbf e}_i \times {\mathbf e}_j }$

$\mathbf u \wedge \mathbf v = \sum_{i<j}{ \begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix} {\mathbf e}_i \wedge {\mathbf e}_j }$

Without justification or historical context, traditional linear algebra texts will often define the determinant as the first step of an elaborate sequence of definitions and theorems leading up to the solution of linear systems, Cramer's rule and matrix inversion.

An alternative treatment is to axiomatically introduce the wedge product, and then demonstrate that this can be used directly to solve linear systems. This is shown below, and does not require sophisticated math skills to understand.

It is then possible to define determinants as nothing more than the coefficients of the wedge product in terms of "unit k-vectors" ( ${\mathbf e}_i \wedge {\mathbf e}_j$ terms) expansions as above.

A one by one determinant is the coefficient of $\mathbf{e}_1$ for an $\mathbb R^1$ 1-vector.

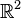A two-by-two determinant is the coefficient of $\mathbf{e}_1 \wedge \mathbf{e}_2$ for an $\mathbb R^2$ bivector

A three-by-three determinant is the coefficient of $\mathbf{e}_1 \wedge \mathbf{e}_2 \wedge \mathbf{e}_3$ for an $\mathbb R^3$ trivector

...

When linear system solution is introduced via the wedge product, Cramer's rule follows as a side effect, and there is no need to lead up to the end results with definitions of minors, matrices, matrix invertibility, adjoints, cofactors, Laplace expansions, theorems on determinant multiplication and row column exchanges, and so forth.

[edit] Equation of a plane

For the plane of all points ${\mathbf r}$ through the plane passing through three independent points ${\mathbf r}_0$ , ${\mathbf r}_1$ , and ${\mathbf r}_2$ , the normal form of the equation is

$(({\mathbf r}_2 - {\mathbf r}_0) \times ({\mathbf r}_1 - {\mathbf r}_0)) \cdot ({\mathbf r} - {\mathbf r}_0) = 0.$

The equivalent wedge product equation is

$({\mathbf r}_2 - {\mathbf r}_0) \wedge ({\mathbf r}_1 - {\mathbf r}_0) \wedge ({\mathbf r} - {\mathbf r}_0) = 0.$

[edit] Projective and rejective components of a vector

For three dimensions the projective and rejective components of a vector with respect to an arbitrary non-zero unit vector, can be expressed in terms of the dot and cross product

$\mathbf v = (\mathbf v \cdot \hat{\mathbf u})\hat{\mathbf u} + \hat{\mathbf u} \times (\mathbf v \times \hat{\mathbf u})$

For the general case the same result can be written in terms of the dot and wedge product and the geometric product of that and the unit vector

$\mathbf v = (\mathbf v \cdot \hat{\mathbf u})\hat{\mathbf u} + (\mathbf v \wedge \hat{\mathbf u}) \hat{\mathbf u}$

It's also worthwhile to point out that this result can also be expressed using right or left vector division as defined by the geometric product

$\mathbf v = (\mathbf v \cdot \mathbf u)\frac{1}{\mathbf u} + (\mathbf v \wedge \mathbf u) \frac{1}{\mathbf u}$

$\mathbf v = \frac{1}{\mathbf u}(\mathbf u \cdot \mathbf v) + \frac{1}{\mathbf u}(\mathbf u \wedge \mathbf v)$

[edit] Area of the parallelogram defined by u and v

If A is the area of the parallelogram defined by u and v, then

$A^2 = {\Vert \mathbf u \times \mathbf v \Vert}^2 = \sum_{i<j}{\begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix}}^2,$

and

$A^2 = -(\mathbf u \wedge \mathbf v)^2 = \sum_{i<j}{\begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix}}^2.$

Note that this squared bivector is a geometric product.

[edit] Angle between two vectors

$({\sin \theta})^2 = \frac{{\Vert \mathbf u \times \mathbf v \Vert}^2}{{\Vert \mathbf u \Vert}^2 {\Vert \mathbf v \Vert}^2}$

$({\sin \theta})^2 = -\frac{(\mathbf u \wedge \mathbf v)^2}{{ \mathbf u }^2 { \mathbf v }^2}$

[edit] Volume of the parallelopiped formed by three vectors

$V^2 = {\Vert (\mathbf u \times \mathbf v) \cdot \mathbf w \Vert}^2 = {\begin{vmatrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \\ \end{vmatrix}}^2$

$V^2 = -(\mathbf u \wedge \mathbf v \wedge \mathbf w)^2 = -\left(\sum_{i<j<k} \begin{vmatrix} u_i & u_j & u_k \\ v_i & v_j & v_k \\ w_i & w_j & w_k \\ \end{vmatrix} \hat{\mathbf e}_i \wedge \hat{\mathbf e}_j \wedge \hat{\mathbf e}_k \right)^2 = \sum_{i<j<k} {\begin{vmatrix} u_i & u_j & u_k \\ v_i & v_j & v_k \\ w_i & w_j & w_k \\ \end{vmatrix}}^2$

[edit] Derivative of a unit vector

It can be shown that a unit vector derivative can be expressed using the cross product

$\frac{d}{dt}\left(\frac{\mathbf r}{\Vert \mathbf r \Vert}\right) = \frac{1}{{\Vert \mathbf r \Vert}^3}\left(\mathbf r \times \frac{d \mathbf r}{dt}\right) \times \mathbf r = \left(\hat{\mathbf r} \times \frac{1}{{\Vert \mathbf r \Vert}} \frac{d \mathbf r}{dt}\right) \times \hat{\mathbf r}$

The equivalent geometric product generalization is

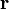$\frac{d}{dt}\left(\frac{\mathbf r}{\Vert \mathbf r \Vert}\right) = \frac{1}{{\Vert \mathbf r \Vert}^3}\mathbf r \left(\mathbf r \wedge \frac{d \mathbf r}{dt}\right) = \frac{1}{{ \mathbf r }}\left(\hat{\mathbf r} \wedge \frac{d \mathbf r}{dt}\right)$

Thus this derivative is the component of $\frac{1}{{\Vert \mathbf r \Vert}}\frac{d \mathbf r}{dt}$ in the direction perpendicular to $\mathbf r$ . In other words this is $\frac{1}{{\Vert \mathbf r \Vert}}\frac{d \mathbf r}{dt}$ minus the projection of that vector onto $\mathbf \hat{r}$ .

This intuitively make sense (but a picture would help) since a unit vector is constrained to circular motion, and any change to a unit vector due to a change in its generating vector has to be in the direction of the rejection of $\mathbf \hat{r}$ from $\frac{d \mathbf r}{dt}$ . That rejection has to be scaled by 1/|r| to get the final result.

When the objective isn't comparing to the cross product, it's also notable that this unit vector derivative can be written

${{ \mathbf r }} \frac{d \hat{\mathbf r}}{dt} = \hat{\mathbf r} \wedge \frac{d \mathbf r}{dt}$

[edit] Some properties and examples

Some fundamental geometric algebra manipulations will be provided below, showing how this vector product can be used in calculation of projections, area, and rotations. How some of these tie together and correlate concepts from other branches of mathematics, such as complex numbers, will also be shown.

In some cases these examples provide details used above in the cross product and geometric product comparisons.

[edit] Inversion of a vector

One of the powerful properties of the Geometric product is that it provides the capability to express the inverse of a non-zero vector. This is expressed by:

$\mathbf a^{-1} = \frac{\mathbf a}{\mathbf a \mathbf a} = \frac{\mathbf a}{\mathbf a \cdot \mathbf a} = \frac{\mathbf a}{\| \mathbf{a} \|^2}.$

[edit] Dot and wedge products defined in terms of the geometric product

Given a definition of the geometric product in terms of the dot and wedge products, adding and subtracting $\mathbf{a} \mathbf{b}$ and $\mathbf{b} \mathbf{a}$ demonstrates that the dot and wedge product of two vectors can also be defined in terms of the geometric product

[edit] The dot product

$\mathbf{a}\cdot\mathbf{b} = \frac{1}{2}(\mathbf{a}\mathbf{b} + \mathbf{b}\mathbf{a})$

This is the symmetric component of the geometric product. When two vectors are colinear the geometric and dot products of those vectors are equal.

As a motivation for the dot product it is normal to show that this quantity occurs in the solution of the length of a general triangle where the third side is the vector sum of the first and second sides $\mathbf{c} = \mathbf{a} + \mathbf{b}$ .

${\Vert \mathbf{c} \Vert}^2 = \sum_{i}(a_i + b_i)^2 = {\Vert \mathbf{a} \Vert}^2 + {\Vert \mathbf{b} \Vert}^2 + 2 \sum_{i}a_i b_i$

The last sum is then given the name the dot product and other properties of this quantity are then shown (projection, angle between vectors, ...).

This can also be expressed using the geometric product

$\mathbf{c}^2 = (\mathbf{a} + \mathbf{b})(\mathbf{a} + \mathbf{b}) = \mathbf{a}^2 + \mathbf{b}^2 + (\mathbf{a}\mathbf{b} + \mathbf{b}\mathbf{a})$

By comparison, the following equality exists

$\sum_{i}a_i b_i = \frac{1}{2}(\mathbf{a}\mathbf{b} + \mathbf{b}\mathbf{a})$ .

Without requiring expansion by components one can define the dot product exclusively in terms of the geometric product due to its properties of contraction, distribution and associativity. This is arguably a more natural way to define the geometric product, especially since the wedge product is not familiar to many people with traditional vector algebra background, and there is no immediate requirement to add two dissimilar terms (ie: scalar and bivector).

[edit] The wedge product

$\mathbf{a}\wedge\mathbf{b} = \frac{1}{2}(\mathbf{a}\mathbf{b} - \mathbf{b}\mathbf{a})$

This is the antisymmetric component of the geometric product. When two vectors are orthogonal the geometric and wedge products of those vectors are equal.

Switching the order of the vectors negates this antisymmetric geometric product component, and contraction property shows that this is zero if the vectors are equal. These are the defining properties of the wedge product.

[edit] Note on symmetric and antisymmetric dot and wedge product formulas

A generalization of the dot product that allows computation of the component of a vector "in the direction" of a plane (bivector), or other k-vectors can be found below. Since the signs change depending on the grades of the terms being multiplied, care is required with the formulas above to ensure that they are only used for a pair of vectors.

[edit] Dot and wedge products compared to the real and imaginary parts of a complex number

Reversing the order of multiplication of two vectors has the effect of the inverting the sign of just the wedge product term of the geometric product.

It is not a coincidence that this is a similar operation to the conjugate operation of complex numbers.

The reverse of a product is written in the following fashion

${\mathbf{b} \mathbf{a}} = ({\mathbf{a} \mathbf{b}})^\dagger$

${\mathbf{c} \mathbf{b} \mathbf{a}} = ({\mathbf{a} \mathbf{b} \mathbf{c}})^\dagger$

Thus, the dot product is

$\mathbf{a}\cdot\mathbf{b} = \frac{1}{2}(\mathbf{a}\mathbf{b} + ({\mathbf{a} \mathbf{b}})^\dagger)$

This is the symmetric component of the geometric product. When two vectors are colinear the geometric and dot products of those vectors are equal. The antisymmetric component is represented by the wedge product:

$\mathbf{a}\wedge\mathbf{b} = \frac{1}{2}(\mathbf{a}\mathbf{b} - ({\mathbf{a} \mathbf{b}})^\dagger)$

These symmetric and antisymmetric components extract the scalar and bivector components of a geometric product in the same fashion as the real and imaginary components of a complex number are extracted by its symmetric and antisymmetric components

$\mathrm{Re}(z) = \frac{1}{2}(z + \bar{z})$

$\mathrm{Im}(z) = \frac{1}{2}(z - \bar{z})$

This extraction of components also applies to higher order geometric product terms. For example

$\mathbf{a}\wedge\mathbf{b}\wedge \mathbf{c} = \frac{1}{2}(\mathbf{a}\mathbf{b}\mathbf{c} - ({\mathbf{a} \mathbf{b}} \mathbf{c})^\dagger) = \frac{1}{2}(\mathbf{b}\mathbf{c}\mathbf{a} - ({\mathbf{b} \mathbf{c}} \mathbf{a})^\dagger) = \frac{1}{2}(\mathbf{c}\mathbf{a}\mathbf{b} - ({\mathbf{c} \mathbf{a}} \mathbf{b})^\dagger)$

[edit] Orthogonal decomposition of a vector

Using the Gram-Schmidt process a single vector can be decomposed into two components with respect to a reference vector, namely the projection onto a unit vector in a reference direction, and the difference between the vector and that projection.

With, $\mathbf \hat{u} = \mathbf u / {\Vert \mathbf u \Vert}$ , the projection of $\mathbf v$ onto $\mathbf \hat{u}$ is

$\mathrm{Proj}_{\mathbf{\hat{u}}}\,\mathbf{v} = \mathbf \hat{u} (\mathbf \hat{u} \cdot \mathbf v)$

Orthogonal to that vector is the difference, designated the rejection,

$\mathbf v - \mathbf \hat{u} (\mathbf \hat{u} \cdot \mathbf v) = \frac{1}{{\Vert \mathbf u \Vert}^2} ( {\Vert \mathbf u \Vert}^2 \mathbf v - \mathbf u (\mathbf u \cdot \mathbf v))$

The rejection can be expressed as a single geometric algebraic product in a few different ways

$\frac{ \mathbf u }{{\mathbf u}^2} ( \mathbf u \mathbf v - \mathbf u \cdot \mathbf v) = \frac{1}{\mathbf u} ( \mathbf u \wedge \mathbf v ) = \mathbf \hat{u} ( \mathbf \hat{u} \wedge \mathbf v ) = ( \mathbf v \wedge \mathbf \hat{u} ) \mathbf \hat{u}$

The similarity in form between the projection and the rejection is notable. The sum of these recovers the original vector

$\mathbf v = \mathbf \hat{u} (\mathbf \hat{u} \cdot \mathbf v) + \mathbf \hat{u} ( \mathbf \hat{u} \wedge \mathbf v )$

Here the projection is in its customary vector form. An alternate formulation is possible that puts the projection in a form that differs from the usual vector formulation

$\mathbf v = \mathbf \frac{1}{\mathbf u} (\mathbf {u} \cdot \mathbf v) + \frac{1}{\mathbf u} ( \mathbf {u} \wedge \mathbf v ) = \mathbf (\mathbf {v} \cdot \mathbf u) \frac{1}{\mathbf u} + ( \mathbf v \wedge \mathbf u ) \frac{1}{\mathbf u}$

[edit] A quicker way to the end result

Working backwards from the end result, it can be observed that this orthogonal decomposition result can in fact follow more directly from the definition of the geometric product itself.

$\mathbf v = \mathbf \hat{u} \mathbf \hat{u} \mathbf v = \mathbf \hat{u} (\mathbf \hat{u} \cdot \mathbf v + \mathbf \hat{u} \wedge \mathbf v )$

With this approach, the original geometrical consideration is not necessarily obvious, but it is a much quicker way to get at the same algebraic result.

However, the hint that one can work backwards, coupled with the knowledge that the wedge product can be used to solve sets of linear equations (see: [1] ), the problem of orthogonal decomposition can be posed directly,

Let $\mathbf v = a \mathbf u + \mathbf x$ , where $\mathbf u \cdot \mathbf x = 0$ . To discard the portions of $\mathbf v$ that are colinear with $\mathbf u$ , take the wedge product

$\mathbf u \wedge \mathbf v = \mathbf u \wedge (a \mathbf u + \mathbf x) = \mathbf u \wedge \mathbf x$

Here the geometric product can be employed

$\mathbf u \wedge \mathbf v = \mathbf u \wedge \mathbf x = \mathbf u \mathbf x - \mathbf u \cdot \mathbf x = \mathbf u \mathbf x$

Because the geometric product is invertible, this can be solved for x

$\mathbf x = \frac{1}{\mathbf u}(\mathbf u \wedge \mathbf v)$

The same techniques can be applied to similar problems, such as calculation of the component of a vector in a plane and perpendicular to the plane.

[edit] Area of parallelogram spanned by two vectors

The area of a parallelogram spanned between one vector and another equals the length of one of those vectors multiplied by the length of the rejection of that vector from the second.

$A(u,v) = \Vert \mathbf u \Vert \Vert \hat{\mathbf u} ( \hat{\mathbf u} \wedge \mathbf v ) \Vert = \Vert \hat{\mathbf u} ( \mathbf u \wedge \mathbf v ) \Vert$

The length of this vector is the area of the spanned parallelogram, and in the square is

$A^2 = (\hat{\mathbf u}( \mathbf u \wedge {\mathbf v} ) ) (\hat{\mathbf u} ( {\mathbf u} \wedge \mathbf v )) = (( \mathbf v \wedge {\mathbf u} ) \hat{\mathbf u}) (\hat{\mathbf u} ( {\mathbf u} \wedge \mathbf v )) = ( \mathbf v \wedge \mathbf u ) ( \mathbf u \wedge \mathbf v ) = -(\mathbf u \wedge \mathbf v )^2$

There are a couple things of note here. One is that the area can easily be expressed in terms of the square of a bivector. The other is that the square of a bivector has the same property as a purely imaginary number, a negative square.

[edit] Expansion of a bivector and a vector rejection in terms of the standard basis

If a vector is factored directly into projective and rejective terms using the geometric product $\mathbf v = \frac{1}{\mathbf u}( \mathbf u \cdot \mathbf v + \mathbf u \wedge \mathbf v)$ , then it is not necessarily obvious that the rejection term, a product of vector and bivector is even a vector. Expansion of the vector bivector product in terms of the standard basis vectors has the following form

Let $\mathbf r = \frac{1}{\mathbf u} ( \mathbf u \wedge \mathbf v ) = \frac{\mathbf u}{\mathbf u^2} ( \mathbf u \wedge \mathbf v ) = \frac{1}{{\Vert \mathbf u \Vert}^2} \mathbf u ( \mathbf u \wedge \mathbf v )$

It can be shown that

$\mathbf r = \frac{1}{{\Vert{\mathbf u}\Vert}^2} \sum_{i<j}\begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix} \begin{vmatrix}u_i & u_j\\ \mathbf e_i & \mathbf e_j\end{vmatrix}$

(a result that can be shown more easily straight from $\mathbf r = \mathbf v - \mathbf \hat{u} (\mathbf \hat{u} \cdot \mathbf v)$ ).

The rejective term is perpendicular to $\mathbf u$ , since $\begin{vmatrix}u_i & u_j\\ u_i & u_j\end{vmatrix} = 0$ implies $\mathbf r \cdot \mathbf u = \mathbf 0$ .

The magnitude of 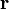$\mathbf r$ , is

${\Vert \mathbf r \Vert}^2 = \mathbf r \cdot \mathbf v = \frac{1}{{\Vert{\mathbf u}\Vert}^2} \sum_{i<j}\begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix}^2$ .

So, the quantity

${\Vert \mathbf r \Vert}^2 {\Vert{\mathbf u}\Vert}^2 = \sum_{i<j}\begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix}^2$

is the squared area of the parallelogram formed by $\mathbf u$ and $\mathbf v$ .

It is also noteworthy that the bivector can be expressed as

$\mathbf u \wedge \mathbf v = \sum_{i<j}{ \begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix} \mathbf e_i \wedge \mathbf e_j }$ .

Thus is it natural, if one considers each term $\mathbf e_i \wedge \mathbf e_j$ as a basis vector of the bivector space, to define the (squared) "length" of that bivector as the (squared) area.

Going back to the geometric product expression for the length of the rejection $\frac{1}{\mathbf u} ( \mathbf u \wedge \mathbf v )$ we see that the length of the quotient, a vector, is in this case is the "length" of the bivector divided by the length of the divisor.

This may not be a general result for the length of the product of two k-vectors, however it is a result that may help build some intuition about the significance of the algebraic operations. Namely,

When a vector is divided out of the plane (parallelogram span) formed from it and another vector, what remains is the perpendicular component of the remaining vector, and its length is the planar area divided by the length of the vector that was divided out.

[edit] Projection and rejection of a vector onto and perpendicular to a plane

Like vector projection and rejection, higher dimensional analogs of that calculation are also possible using the geometric product.

As an example, one can calculate the component of a vector perpendicular to a plane and the projection of that vector onto the plane.

Let $\mathbf w = a \mathbf u + b \mathbf v + \mathbf x$ , where $\mathbf u \cdot \mathbf x = \mathbf v \cdot \mathbf x = 0$ . As above, to discard the portions of $\mathbf w$ that are colinear with $\mathbf u$ or $\mathbf v$ , take the wedge product

$\mathbf w \wedge \mathbf u \wedge \mathbf v = (a \mathbf u + b \mathbf v + \mathbf x) \wedge \mathbf u \wedge \mathbf v = \mathbf x \wedge \mathbf u \wedge \mathbf v.$

Having done this calculation with a vector projection, one can guess that this quantity equals $\mathbf x (\mathbf u \wedge \mathbf v)$ . One can also guess there is a vector and bivector dot product like quantity such that the allows the calculation of the component of a vector that is in the "direction of a plane". Both of these guesses are correct, and the validating these facts is worthwhile. However, skipping ahead slightly, this to be proved fact allows for a nice closed form solution of the vector component outside of the plane:

$\mathbf x = (\mathbf w \wedge \mathbf u \wedge \mathbf v)\frac{1}{\mathbf u \wedge \mathbf v} = \frac{1}{\mathbf u \wedge \mathbf v}(\mathbf u \wedge \mathbf v \wedge \mathbf w).$

Notice the similarities between this planar rejection result a the vector rejection result. To calculation the component of a vector outside of a plane we take the volume spanned by three vectors (trivector) and "divide out" the plane.

Independent of any use of the geometric product it can be shown that this rejection in terms of the standard basis is

$\mathbf x = \frac{1}{(A_{u,v})^2} \sum_{i<j<k} \begin{vmatrix}w_i & w_j & w_k \\u_i & u_j & u_k \\v_i & v_j & v_k \\\end{vmatrix} \begin{vmatrix}u_i & u_j & u_k \\v_i & v_j & v_k \\ {\mathbf e}_i & {\mathbf e}_j & {\mathbf e}_k \\ \end{vmatrix}$

where

$(A_{u,v})^2 = \sum_{i<j} \begin{vmatrix}u_i & u_j\\v_i & v_j\end{vmatrix} = -(\mathbf u \wedge \mathbf v)^2$

is the squared area of the parallelogram formed by $\mathbf u$ , and $\mathbf v$ .

The (squared) magnitude of $\mathbf x$ is

${\Vert \mathbf x \Vert}^2 = \mathbf x \cdot \mathbf w = \frac{1}{(A_{u,v})^2} \sum_{i<j<k} {\begin{vmatrix}w_i & w_j & w_k \\u_i & u_j & u_k \\v_i & v_j & v_k \\\end{vmatrix}}^2$

Thus, the (squared) volume of the parallelopiped (base area times perpendicular height) is

$\sum_{i<j<k} {\begin{vmatrix}w_i & w_j & w_k \\u_i & u_j & u_k \\v_i & v_j & v_k \\\end{vmatrix}}^2$

Note the similarity in form to the w, u,v trivector itself

$\sum_{i<j<k} {\begin{vmatrix}w_i & w_j & w_k \\u_i & u_j & u_k \\v_i & v_j & v_k \\\end{vmatrix}} {\mathbf e}_i \wedge {\mathbf e}_j \wedge {\mathbf e}_k$

which, if you take the set of ${\mathbf e}_i \wedge {\mathbf e}_j \wedge {\mathbf e}_k$ as a basis for the trivector space, suggests this is the natural way to define the length of a trivector. Loosely speaking the length of a vector is a length, length of a bivector is area, and the length of a trivector is volume.

[edit] Product of a vector and a bivector ("dot product" of a plane and a vector)

In order to justify the normal to a plane result above, a general examination of the product of a vector and bivector is required. Namely,

$\mathbf w (\mathbf u \wedge \mathbf v) = \sum_{i,j<k}w_i {\mathbf e}_i {\begin{vmatrix}u_j & u_k \\v_j & v_k \\\end{vmatrix}} {\mathbf e}_j \wedge {\mathbf e}_k$

This has two parts, the vector part where $i = j$ or $i = k$ , and the trivector parts where no indexes equal. After some index summation trickery, and grouping terms and so forth, this is

$\mathbf w (\mathbf u \wedge \mathbf v) = \sum_{i<j}(w_i {\mathbf e}_j - w_j {\mathbf e}_i ) {\begin{vmatrix}u_i & u_j \\v_i & v_j \\\end{vmatrix}} + \sum_{i<j<k} {\begin{vmatrix}w_i & w_j & w_k \\ u_i & u_j & u_k \\v_i & v_j & v_k \\\end{vmatrix}} {\mathbf e}_i \wedge {\mathbf e}_j \wedge {\mathbf e}_k$

The trivector term is $\mathbf w \wedge \mathbf u \wedge \mathbf v$ . Expansion of $(\mathbf u \wedge \mathbf v) \mathbf w$ yields the same trivector term (it is the completely symmetric part), and the vector term is negated. Like the geometric product of two vectors, this geometric product can be grouped into symmetric and antisymmetric parts, one of which is a pure k-vector. In analogy the antisymmetric part of this product can be called a generalized dot product, and is roughly speaking the dot product of a "plane" (bivector), and a vector.

The properties of this generalized dot product remain to be explored, but first here is a summary of the notation

$\mathbf w (\mathbf u \wedge \mathbf v) = \mathbf w \cdot (\mathbf u \wedge \mathbf v) + \mathbf w \wedge \mathbf u \wedge \mathbf v$

$(\mathbf u \wedge \mathbf v) \mathbf w = - \mathbf w \cdot (\mathbf u \wedge \mathbf v) + \mathbf w \wedge \mathbf u \wedge \mathbf v$

$\mathbf w \wedge \mathbf u \wedge \mathbf v = \frac{1}{2}(\mathbf w (\mathbf u \wedge \mathbf v) + (\mathbf u \wedge \mathbf v) \mathbf w)$

$\mathbf w \cdot (\mathbf u \wedge \mathbf v) = \frac{1}{2}(\mathbf w (\mathbf u \wedge \mathbf v) - (\mathbf u \wedge \mathbf v) \mathbf w)$

Let $\mathbf w = \mathbf x + \mathbf y$ , where $\mathbf x = a \mathbf u + b \mathbf v$ , and $\mathbf y \cdot \mathbf u = \mathbf y \cdot \mathbf v = \mathbf 0$ . Expressing $\mathbf w$ and the $\mathbf u \wedge \mathbf v$ , products in terms of these components is

$\mathbf w (\mathbf u \wedge \mathbf v) = \mathbf x (\mathbf u \wedge \mathbf v) + \mathbf y (\mathbf u \wedge \mathbf v) = \mathbf x \cdot (\mathbf u \wedge \mathbf v) + \mathbf y \cdot (\mathbf u \wedge \mathbf v) + \mathbf y \wedge \mathbf u \wedge \mathbf v$

With the conditions and definitions above, and some manipulation, it can be shown that the term $\mathbf y \cdot (\mathbf u \wedge \mathbf v) = \mathbf 0$ , which then justifies the previous solution of the normal to a plane problem. Since the vector term of the vector bivector product the name dot product is zero when the vector is perpendicular to the plane (bivector), and this vector, bivector "dot product" selects only the components that are in the plane, so in analogy to the vector-vector dot product this name itself is justified by more than the fact this is the non-wedge product term of the geometric vector-bivector product.

[edit] Generalized inner and outer product

While the cross product can only be defined in a three-dimensional space, the inner and outer products can be generalized to any dimensional $\mathcal G_{p,q,r}$ .

Let $\mathbf{a},\, \mathbf{A}_{\langle k \rangle}$ be a vector and a homogeneous multivector of grade k, respectively. Their inner product is then

$\mathbf a \cdot \mathbf A_{\langle k \rangle} = {1 \over 2} \, \left ( \mathbf a \, \mathbf A_{\langle k \rangle} + (-1)^{k+1} \, \mathbf{A}_{\langle k \rangle} \, \mathbf{a} \right ) = (-1)^{k+1} \mathbf A_{\langle k \rangle} \cdot \mathbf{a}$

and the outer product is

$\mathbf a \wedge \mathbf A_{\langle k \rangle} = {1 \over 2} \, \left ( \mathbf a \, \mathbf A_{\langle k \rangle} - (-1)^{k+1} \, \mathbf{A}_{\langle k \rangle} \, \mathbf{a} \right ) = (-1)^{k} \mathbf A_{\langle k \rangle} \wedge \mathbf{a}$

[edit] Complex numbers

There is a one to one correspondence between the geometric product of two $\mathbb{R}^2$ vectors and the field of complex numbers.

Writing, a vector in terms of its components, and left multiplying by the unit vector $\mathbf {e_1}$ yields

$Z = \mathbf {e_1} \mathbf P = \mathbf {e_1} ( x \mathbf {e_1} + y \mathbf {e_2}) = x (1) + y (\mathbf {e_1} \mathbf {e_2}) = x (1) + y (\mathbf {e_1} \wedge \mathbf {e_2})$

The unit scalar and unit bivector pair $1, \mathbf {e_1} \wedge \mathbf {e_2}$ can be considered an alternate basis for a two dimensional vector space. This alternate vector representation is closed with respect to the geometric product

$Z_1 Z_2 = \mathbf {e_1} ( x_1 \mathbf {e_1} + y_1 \mathbf {e_2}) \mathbf {e_1} ( x_2 \mathbf {e_1} + y_2 \mathbf {e_2}) = ( x_1 + y_1 \mathbf {e_1} \mathbf {e_2}) ( x_2 + y_2 \mathbf {e_1} \mathbf {e_2}) = x_1 x_2 + y_1 y_2 (\mathbf {e_1} \mathbf {e_2}) (\mathbf {e_1} \mathbf {e_2}) + (x_1 y_2 + x_2 y_1) \mathbf {e_1} \mathbf {e_2}$

This closure can be observed after calculation of the square of the unit bivector above, a quantity

$(\mathbf {e_1} \wedge \mathbf {e_2})^2 = \mathbf {e_1} \mathbf {e_2} \mathbf {e_1} \mathbf {e_2} = - \mathbf {e_1} \mathbf {e_1} \mathbf {e_2} \mathbf {e_2} = -1$

that has the characteristics of the complex number $i 2 = - 1$ .

This fact allows the simplification of the product above to

$Z_1 Z_2 = (x_1 x_2 - y_1 y_2) + (x_1 y_2 + x_2 y_1) (\mathbf {e_1} \wedge \mathbf {e_2})$

Thus what is traditionally the defining, and arguably arbitrary seeming, rule of complex number multiplication, is found to follow naturally from the higher order structure of the geometric product, once that is applied to a two dimensional vector space.

It is also informative to examine how the length of a vector can be represented in terms of a complex number. Taking the square of the length

$\mathbf P \cdot \mathbf P = ( x \mathbf {e_1} + y \mathbf {e_2}) \cdot ( x \mathbf {e_1} + y \mathbf {e_2}) = (\mathbf {e_1} Z) \mathbf {e_1} Z = (( x - y \mathbf {e_1} \mathbf {e_2}) \mathbf {e_1}) \mathbf {e_1} Z = ( x - y (\mathbf {e_1} \wedge \mathbf {e_2})) Z$

This right multiplication of a vector with $\mathbf {e_1}$ , is named the conjugate

$\overline{Z} = x - y (\mathbf {e_1} \wedge \mathbf {e_2})$ .

And with that definition, the length of the original vector can be expressed as

$\mathbf P \cdot \mathbf P = \overline{Z}Z$

This is also a natural definition of the length of a complex number, given the fact that the complex numbers can be considered an isomorphism with the two dimensional Euclidean vector space.

[edit] Rotation in an arbitrarily oriented plane

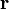A point $\mathbf P$ , of radius $\mathbf r$ , located at an angle $θ$ from the vector $\mathbf \hat{u}$ in the direction from $\mathbf u$ to $\mathbf v$ , can be expressed as

$\mathbf P = r( \mathbf \hat{u} \cos{\theta} + \frac{\mathbf \hat{u} (\mathbf \hat{u} \wedge \mathbf v)}{\Vert \mathbf \hat{u} (\mathbf \hat{u} \wedge \mathbf v) \Vert} \sin{\theta}) = r \mathbf \hat{u} ( \cos{\theta} + \frac{(\mathbf {u} \wedge \mathbf v)}{\Vert \mathbf \hat{u} (\mathbf {u} \wedge \mathbf v) \Vert} \sin{\theta})$

Writing $\mathbf{I}_{\mathbf{u},\mathbf{v}} = \frac{\mathbf {u} \wedge \mathbf v}{\Vert \mathbf \hat{u} (\mathbf {u} \wedge \mathbf v) \Vert}$ , the square of this bivector has the property ${\mathbf{I}_{\mathbf{u},\mathbf{v}}}^2 = -1$ of the imaginary unit complex number.

This allows the point to be specified as a complex exponential

$= \mathbf \hat{u} r ( \cos\theta + \mathbf{I}_{\mathbf{u},\mathbf{v}} \sin\theta ) = \mathbf \hat{u} r \exp( \mathbf{I}_{\mathbf{u},\mathbf{v}} \theta )$

Complex numbers could be expressed in terms of the 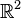$\mathbb R^2$ unit bivector $\mathbf {e_1} \wedge \mathbf {e_2}$ . However this isomorphism really only requires a pair of linearly independent vectors in a plane (of arbitrary dimension).

[edit] Quaternions

Like complex numbers, quaternions may be written as a multivector with scalar and bivector components (a 0,2-multivector).

$q = \alpha + \mathbf{B}$

Where the complex number has one bivector component, and the quaternions have three.

One can describe quaternions as 0,2-multivectors where the basis for the bivector part is left-handed. There isn't really anything special about quaternion multiplication, or complex number multiplication, for that matter. Both are just a specific examples of a 0,2-multivector multiplication. Other quaternion operations can also be found to have natural multivector equivalents. The most important of which is likely the quaternion conjugate, since it implies the norm and the inverse. As a multivector, like complex numbers, the conjugate operation is reversal:

$\overline{q} = q^\dagger = \alpha - \mathbf{B}$

Thus ${\vert{q}\vert}^2 = q\overline{q} = \alpha^2 - \mathbf{B}^2$ . Note that this norm is a positive definite as expected since a bivector square is negative.

To be more specific about the left-handed basis property of quaternions one can note that the quaternion bivector basis is usually defined in terms of the following properties

$\mathbf{i}^2 = \mathbf{j}^2 = \mathbf{k}^2 = -1$

$\mathbf{i}\mathbf{j} = -\mathbf{j}\mathbf{i}, \mathbf{i}\mathbf{k} = -\mathbf{k}\mathbf{i}, \mathbf{j}\mathbf{k} = -\mathbf{k}\mathbf{j}$

$\mathbf{i}\mathbf{j} = \mathbf{k}$

The first two properties are satisfied by any set of orthogonal unit bivectors for the space. The last property, which could also be written $\mathbf{i}\mathbf{j}\mathbf{k} = -1$ , amounts to a choice for the orientation of this bivector basis of the 2-vector part of the quaternion.

As an example suppose one picks

$\mathbf{i} = \mathbf{e}_2\mathbf{e}_3$

$\mathbf{j} = \mathbf{e}_3\mathbf{e}_1$

Then the third bivector required to complete the basis set subject to the properties above is

$\mathbf{i}\mathbf{j} = \mathbf{e}_2\mathbf{e}_1 = \mathbf{k}$ .

Suppose that, instead of the above, one picked a slightly more natural bivector basis, the duals of the unit vectors obtained by multiplication with the pseudoscalar ( $\mathbf{e}_1\mathbf{e}_2\mathbf{e}_3\mathbf{e}_i$ ). These bivectors are

$\mathbf{i}=\mathbf{e}_2\mathbf{e}_3, \mathbf{j}=\mathbf{e}_3\mathbf{e}_1, \mathbf{k}=\mathbf{e}_1\mathbf{e}_2$ .

A 0,2-multivector with this as the basis for the bivector part would have properties similar to the standard quaternions (anti-commutative unit quaternions, negation for unit quaternion square, same congugate, norm and inversion operations, ...), however the triple product would have the value $\mathbf{i}\mathbf{j}\mathbf{k} = 1$ , instead of $- 1$ .

[edit] Cross product as outer product

The cross product of traditional vector algebra (on $\mathbb{R}^3$ ) find its place in geometric algebra $\mathcal{G}_3$ as a scaled outer product

$\mathbf{a}\times\mathbf{b} = -i(\mathbf{a}\wedge\mathbf{b})$

(this is antisymmetric). Relevant is the distinction between axial and polar vectors in vector algebra, which is natural in geometric algebra as the mere distinction between vectors and bivectors (elements of grade two).

The $i$ here is a unit pseudoscalar of Euclidean 3-space, which establishes a duality between the vectors and the bivectors, and is named so because of the expected property

$i^2 = (\mathbf {e_1}\mathbf {e_2}\mathbf {e_3})^2 = \mathbf {e_1}\mathbf {e_2}\mathbf {e_3}\mathbf {e_1}\mathbf {e_2}\mathbf {e_3} = -\mathbf {e_1}\mathbf {e_2}\mathbf {e_1}\mathbf {e_3}\mathbf {e_2}\mathbf {e_3} = \mathbf {e_1}\mathbf {e_1}\mathbf {e_2}\mathbf {e_3}\mathbf {e_2}\mathbf {e_3} = -\mathbf {e_3}\mathbf {e_2}\mathbf {e_2}\mathbf {e_3} = -1$

The equivalence of the $\mathbb{R}^3$ cross product and the wedge product expression above can be confirmed by direct multiplication of $-i = -\mathbf {e_1}\mathbf {e_2}\mathbf {e_3}$ with a determinant expansion of the wedge product

$\mathbf u \wedge \mathbf v = \sum_{1<=i<j<=3}(u_i v_j - v_i u_j) \mathbf {e_i} \wedge \mathbf {e_j} = \sum_{1<=i<j<=3}(u_i v_j - v_i u_j) \mathbf {e_i} \mathbf {e_j}$

See also Cross product#Cross product as an exterior product. Essentially, the geometric product of a bivector and the pseudoscalar of Euclidean 3-space provides a method of calculation of the hodge dual.

[edit] Intersection of a line and a plane

As a meaningful result one can consider a fixed non-zero vector $\mathbf v$ , from a point chosen as the origin, in the usual 3-D Euclidean space, $\mathbb{R}^3$ . The set of all vectors $\mathbf x$ such that $\mathbf x \wedge \mathbf v = \mathbf B$ , $\mathbf B$ denoting a given bivector containing $\mathbf v$ , determines a line $l$ parallel to $\mathbf v$ . Since $\mathbf B$ is a directed area, $l$ is uniquely determined with respect to the chosen origin. The set of all vectors $\mathbf x$ such that $\mathbf x \cdot \mathbf v = s$ , $s$ denoting a given (real) scalar, determines a plane P orthogonal to $\mathbf v$ . Again, P is uniquely determined with respect to the chosen origin. The two information pieces, $\mathbf B$ and $s$ , can be set independently of one another. Now, what is (if any) the vector $\mathbf x$ that satisfies the system { $\mathbf x \wedge \mathbf v = \mathbf B$ , $\mathbf x \cdot \mathbf v = s$ }? Geometrically, the answer is plain: it is the vector that departs from the origin and arrives at the intersection of $l$ and P. By geometric algebra, even the algebraic answer is simple:

$\mathbf x \mathbf v = s + \mathbf B \implies \mathbf x = (s + \mathbf B )/ \mathbf v = (s + \mathbf B ) \mathbf v$ ^-1.

Note that the division by a vector transforms the multivector $s + \mathbf B$ into the sum of two vectors. Namely, $s \mathbf v$ ^-1 is the projection of $\mathbf x$ on $\mathbf v$ , and $\mathbf B \mathbf v$ ^-1 is the rejection of $\mathbf x$ from $\mathbf v$ (i.e. the component of $\mathbf x$ orthogonal to $\mathbf v$ ). Note also that the structure of the solution does not depend on the chosen origin.

[edit] Torque

Torque is generally defined as the magnitude of the perpendicular force component times distance, or work per unit angle.

Suppose a circular path in an arbitrary plane containing orthonormal vectors $\hat{\mathbf u}$ and $\hat{\mathbf v}$ is parameterized by angle.

$\mathbf r = r(\hat{\mathbf u} \cos \theta + \hat{\mathbf v} \sin \theta) = r \hat{\mathbf u}(\cos \theta + \hat{\mathbf u} \hat{\mathbf v} \sin \theta)$

By designating the unit bivector of this plane as the imaginary number

$\mathbf{i} = \hat{\mathbf u} \hat{\mathbf v} = \hat{\mathbf u} \wedge \hat{\mathbf v}$

$\mathbf{i}^2 = -1$

this path vector can be conveniently written in complex exponential form

$\mathbf r = r \hat{\mathbf u} e^{\mathbf{i} \theta}$

and the derivative with respect to angle is

$\frac{d \mathbf r}{d\theta} = r \hat{\mathbf u} \mathbf{i} e^{\mathbf{i} \theta} = \mathbf{r} \mathbf{i}$

So the torque, the rate of change of work W, due to a force F, is

$\tau = \frac{dW}{d\theta} = \mathbf F \cdot \frac{d \mathbf r}{d\theta} = \mathbf F \cdot (\mathbf{r} \mathbf{i})$

Unlike the cross product description of torque, $\mathbf \tau = \mathbf r \times \mathbf F$ , the geometric-algebra description does not introduce a vector in the normal direction; a vector that doesn't exist in two and that is not unique in greater than three dimensions. The unit bivector describes the plane and the orientation of the rotation, and the sense of the rotation is relative to the angle between the vectors $\mathbf{\hat{u}}$ and $\mathbf{\hat{v}}$ .

[edit] Expanding the result in terms of components

At a glance this doesn't appear much like the familiar torque as a determinant or cross product, but this can be expanded to demonstrate its equivalence (the cross product is hiding there in the bivector $\mathbf i = \hat{\mathbf u} \wedge \hat{\mathbf v}$ ). Expanding the position vector in terms of the planar unit vectors

$\mathbf r \mathbf i = \left( r_u \hat{\mathbf u} + r_v \hat{\mathbf v} \right) \hat{\mathbf u} \hat{\mathbf v} = r_u \hat{\mathbf v} - r_v \hat{\mathbf u}$

and expanding the force by components in the same direction plus the possible perpendicular remainder term

$\mathbf F = F_u \hat{\mathbf u} + F_v \hat{\mathbf v} + \mathbf{F}_{\perp \hat{\mathbf u},\hat{\mathbf v}}$

and then taking dot products yields is the torque

$\tau = \mathbf F \cdot (\mathbf{r} \mathbf{i}) = r_u F_v - r_v F_u$ .

This determinant may be familiar from derivations with $\mathbf{\hat{u}} = \mathbf{e}_1$ , and $\mathbf{\hat{v}} = \mathbf{e}_2$ (See the Feynman lectures Volume I for example).

[edit] Geometrical description

When the magnitude of the "rotational arm" is factored out, the torque can be written as

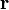$\tau = \mathbf F \cdot (\mathbf{r} \mathbf{i}) = |\mathbf{r}| (\mathbf F \cdot (\mathbf{\hat{r}} \mathbf{i}))$

The vector $\mathbf{\hat{r}} \mathbf{i}$ is the unit vector perpendicular to the $\mathbf{r}$ . Thus the torque can also be described as the product of the magnitude of the rotational arm times the component of the force that is in the direction of the rotation (ie: the work done rotating something depends on length of the lever, and the size of the useful part of the force pushing on it).

[edit] Application of the force to a lever not in the rotation plane

If the rotational arm that the force is applied to is not in the plane of rotation then only the components of the lever arm direction and the component of the force that are in the plane will contribute to the work done. The calculation above allowed for a force applied in an arbitrary direction, so to generalize this, a calculation that discards the component of the level arm direction not in the plane.

When 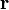$\mathbf{r}$ is allowed to lie outside of the plane of rotation the component in the plane (bivector) 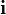$\mathbf{i}$ can be described with the geometric product nicely

$\mathbf{r}_{\mathbf{i}} = (\mathbf{r} \cdot \mathbf{i}) \frac{1}{\mathbf{i}} = -(\mathbf{r} \cdot \mathbf{i}) \mathbf{i}$

Thus, the vector with this magnitude that is perpendicular to this in the plane of the rotation is

$\mathbf{r}_{\mathbf{i}} \mathbf{i} = -(\mathbf{r} \cdot \mathbf{i}) \mathbf{i}^2 = (\mathbf{r} \cdot \mathbf{i})$

and the total torque is thus

$\tau = \mathbf{F} \cdot (\mathbf{r} \cdot \mathbf{i})$

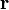This makes sense when once considers that only the dot product part of $\mathbf{r} \mathbf{i} = \mathbf{r} \cdot \mathbf{i} + \mathbf{r} \wedge \mathbf{i}$ contributes to the component of $\mathbf{r}$ in the plane, and when the lever is in the rotational plane this wedge product component of $\mathbf{r} \mathbf{i}$ is zero.

[edit] Matrix inversion and determinants

Matrix inversion (Cramer's rule) and determinants can be naturally expressed in terms of the wedge product.

The use of the wedge product in the solution of linear equations can be quite useful for various geometric product calculations.

Traditionally, instead of using the wedge product, Cramer's rule is usually presented as a generic algorithm that can be used to solve linear equations of the form $\mathbf A \mathbf x = \mathbf b$ (or equivalently to invert a matrix). Namely

$\mathbf x = \frac{1}{|\mathbf A|}\operatorname{adj}(\mathbf A)\mathbf b$ .

This is a useful theoretic result. For numerical problems row reduction with pivots and other methods are more stable and efficient.

When the wedge product is coupled with the Clifford product and put into a natural geometric context, the fact that the determinants are used in the expression of 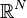${\mathbb R}^N$ parallelogram area and parallelepiped volumes (and higher dimensional generalizations of these) also comes as a nice side effect.

As is also shown below, results such as Cramer's rule also follow directly from the property of the wedge product that it selects non identical elements. The end result is then simple enough that it could be derived easily if required instead of having to remember or look up a rule.

[edit] Two variables example

$\begin{bmatrix}\mathbf a & \mathbf b\end{bmatrix} \begin{bmatrix}x \\ y\end{bmatrix} = \mathbf a x + \mathbf b y = \mathbf c$

Pre and post multiplying by $\mathbf a$ and $\mathbf b$

$( \mathbf a x + \mathbf b y ) \wedge \mathbf b = (\mathbf a \wedge \mathbf b) x = \mathbf c \wedge \mathbf b$

$\mathbf a \wedge ( \mathbf a x + \mathbf b y ) = (\mathbf a \wedge \mathbf b) y = \mathbf a \wedge \mathbf c$

Provided $\mathbf a \wedge \mathbf b \neq 0$ the solution is

$\begin{bmatrix}x \\ y\end{bmatrix} = \frac{1}{\mathbf a \wedge \mathbf b} \begin{bmatrix}\mathbf c \wedge \mathbf b \\ \mathbf a \wedge \mathbf c\end{bmatrix}$

For $\mathbf a, \mathbf b \in {\mathbb R}^2$ , this is Cramer's rule since the $\mathbf{e}_1 \wedge \mathbf{e}_2$ factors of the wedge products

$\mathbf u \wedge \mathbf v = \begin{vmatrix}u_1 & u_2 \\ v_1 & v_2 \end{vmatrix} \mathbf{e}_1 \wedge \mathbf{e}_2$

divide out.

Similarly, for three, or N variables, the same ideas hold

$\begin{bmatrix}\mathbf a & \mathbf b & \mathbf c\end{bmatrix} \begin{bmatrix}x \\ y \\ z\end{bmatrix} = \mathbf d$

$\begin{bmatrix}x \\ y \\ z\end{bmatrix} = \frac{1}{\mathbf a \wedge \mathbf b \wedge \mathbf c} \begin{bmatrix} \mathbf d \wedge \mathbf b \wedge \mathbf c \\ \mathbf a \wedge \mathbf d \wedge \mathbf c \\ \mathbf a \wedge \mathbf b \wedge \mathbf d \end{bmatrix}$

Again, for the three variable three equation case this is Cramer's rule since the $\mathbf{e}_1 \wedge \mathbf{e}_2 \wedge \mathbf{e}_3$ factors of all the wedge products divide out, leaving the familiar determinants.

[edit] A numeric example with three equations and two unknowns

When there are more equations than variables case, if the equations have a solution, each of the k-vector quotients will be scalars

To illustrate here is the solution of a simple example with three equations and two unknowns.

$\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} x + \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} y = \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix}$

The right wedge product with $(1,1,1)$ solves for $x$

$\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \wedge \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} x = \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix} \wedge \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}$

and a left wedge product with $(1,1,0)$ solves for $y$

$\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \wedge \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} y = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} \wedge \begin{bmatrix} 1 \\ 1 \\ 2 \end{bmatrix}.$

Observe that both of these equations have the same factor, so one can compute this only once (if this was zero it would indicate the system of equations has no solution).

Collection of results for $x$ and $y$ yields a Cramers rule like form:

$\begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{(1, 1, 0) \wedge (1, 1, 1)} \begin{bmatrix} (1, 1, 2) \wedge (1, 1, 1) \\ (1, 1, 0) \wedge (1, 1, 2) \end{bmatrix}.$

Writing $\mathbf{e} _i \wedge \mathbf{e} _j = \mathbf{e} _{ij}$ , we have the end result:

$\begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{\mathbf{e}_{13} + \mathbf{e}_{23}} \begin{bmatrix} {-\mathbf{e}_{13} - \mathbf{e}_{23}} \\ {2\mathbf{e}_{13} +2\mathbf{e}_{23}} \\ \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix}.$

[edit] The contraction rule

The connection between Clifford algebras and quadratic forms come from the contraction property. This rule also gives the space a metric defined by the naturally derived inner product. It is to be noted that in geometric algebra in all its generality there is no restriction whatsoever on the value of the scalar, it can very well be negative, even zero (in that case, the possibility of an inner product is ruled out if you require $\langle x, x \rangle \ge 0$ ).

The contraction rule can be put in the form:

$Q(\mathbf a) = \mathbf a^2 = \epsilon_a {\Vert \mathbf a \Vert}^2$

where $\Vert \mathbf a \Vert$ is the modulus of vector a, and $\epsilon_a=0, \, \pm1$ is called the signature of vector a. This is especially useful in the construction of a Minkowski space (the spacetime of special relativity) through $\mathbb{R}_{1,3}$ . In that context, null-vectors are called "lightlike vectors", vectors with negative signature are called "spacelike vectors" and vectors with positive signature are called "timelike vectors" (these last two denominations are exchanged when using $\mathbb{R}_{3,1}$ instead).

[edit] Applications of geometric algebra

A useful example is $\mathbb{R}_{3, 1}$ , and to generate $\mathcal{G}_{3, 1}$ , an instance of geometric algebra sometimes called spacetime algebra.^[1] The electromagnetic field tensor, in this context, becomes just a bivector $\mathbf{E} + i\mathbf{B}$ where the imaginary unit is the volume element, giving an example of the geometric reinterpretation of the traditional "tricks".

Boosts in this Lorenzian metric space have the same expression $e^{\mathbf{\beta}}$ as rotation in Euclidean space, where $\mathbf{\beta}$ is of course the bivector generated by the time and the space directions involved, whereas in the Euclidean case it is the bivector generated by the two space directions, strengthening the "analogy" to almost identity.

[edit] History

The concinnity of geometry and algebra dates as far back at least to Euclid's Elements in the 3rd century B.C.^[2] It was not, however, until 1844 that algebra would be used in a systematic way to describe the geometrical properties and transformations of a space. In that year, Hermann Grassmann introduced the idea of a geometrical algebra in full generality as a certain calculus (analogous to the propositional calculus) which encoded all of the geometrical information of a space. Grassmann's algebraic system could be applied to a number of different kinds of spaces: the chief among them being Euclidean space, affine space, and projective space. Following Grassmann, in 1878 William Kingdon Clifford examined Grassmann's algebraic system alongside the quaternions of William Rowan Hamilton. From his point of view, the quaternions described certain transformations (which he called rotors), whereas Grassmann's algebra described certain properties (or Strecken such as length, area, and volume). His contribution was to define a new product — the geometric product — on an existing Grassmann algebra, which realized the quaternions as living within that algebra. Subsequently Rudolf Lipschitz in 1886 generalized Clifford's interpretation of the quaternions and applied them to the geometry of rotations in n dimensions. Later these developments would lead other 20th-century mathematicians to formalize and explore the properties of the Clifford algebra.

Nevertheless, another revolutionary development of the 19th-century would completely overshadow the geometric algebras: that of vector analysis, developed independently by Josiah Willard Gibbs and Oliver Heaviside. Vector analysis was motivated by James Clerk Maxwell's studies of electromagnetism, and specifically the need to express and manipulate conveniently certain differential equations. Vector analysis had a certain intuitive appeal compared to the rigors of the new algebras. Physicists and mathematicians alike readily adopted it as their geometrical toolkit of choice. Progress on the study of Clifford algebras quietly advanced through the twentieth century, although largely due to the work of abstract algebraists such as Hermann Weyl and Claude Chevalley.

The geometrical approach to geometric algebras has seen a number of 20th-century revivals. In mathematics, Emil Artin's Geometric Algebra discusses the algebra associated with each of a number of geometries, including affine geometry, projective geometry, symplectic geometry, and orthogonal geometry. In physics, geometric algebras have been revived as a "new" way to do classical mechanics and electromagnetism.^[3] David Hestenes reinterpreted the Pauli and Dirac matrices as vectors in ordinary space and spacetime, respectively. In computer graphics, geometric algebras have been revived in order to represent efficiently rotations (and other transformations) on computer hardware.^[4]

[edit] See also

[edit] Notes

^ Cf. Hestenes (1966).
^ Euclid, Books II and VI.
^ Hestenes, et al (1984).
^ Dorst, et al (2007).

[edit] References

Artin, Emil (1957). Geometric Algebra. Interscience Publishers.
Clifford, W. (1878). "Applications of Grassmann's Extensive Algebra". American Journal of Mathematics 1 (4): 350–358. doi:10.2307/2369379.
Leo Dorst, Daniel Fontijne, Stephen Mann, "Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry" (The Morgan Kaufmann Series in Computer Graphics), Morgan Kaufmann (April 19, 2007), ISBN-10: 0123694655, ISBN-13: 978-0123694652.
Grassmann, Hermann (1844). Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik. (The Linear Extension Theory - A new Branch of Mathematics)
Hestenes, David (1966). Space-time Algebra. Gordon and Breach.
David Hestenes and Sobczyk, G., 1984. Clifford Algebra to Geometric Calculus, Springer Verlag ISBN 90-277-1673-0

[edit] Further reading

Baylis, W. E., ed., 1996. Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering. Boston: Birkhäuser.
Baylis, W. E., 2002. Electrodynamics: A Modern Geometric Approach, 2nd ed. Birkhäuser. ISBN 0-8176-4025-8
Nicolas Bourbaki, 1980. Eléments de Mathématique. Algèbre. Chpt. 9, "Algèbres de Clifford". Paris: Hermann.
Hestenes, D., 1999. New Foundations for Classical Mechanics, 2nd ed. Springer Verlag ISBN 0-7923-5302-1
Lasenby, J., Lasenby, A. N., and Doran, C. J. L., 2000, "A Unified Mathematical Language for Physics and Engineering in the 21st Century," Philosophical Transactions of the Royal Society of London A 358: 1-18.
Chris Doran & Anthony Lasenby (2003). Geometric algebra for physicists. Cambridge University Press. ISBN 978-0-521-71595-9.

[edit] External links

[edit] Research groups

Geometric Calculus International. Links to Research groups, Software, and Conferences, worldwide.
Cambridge Geometric Algebra group. Full-text online publications, and other material.
University of Amsterdam group
Geometric Calculus research & development (Arizona State University).
GA-Net blog and newsletter archive. Geometric Algebra/Clifford Algebra development news.

[edit] Online reading

Imaginary Numbers are not Real - the Geometric Algebra of Spacetime. Introduction (Cambridge GA group).
Physical Applications of Geometric Algebra. Final-year undergraduate course (Cambridge GA group; see also 1999 version).
Maths for (Games) Programmers: 5 - Multivector methods. Comprehensive introduction and reference for programmers, from Ian Bell.
A Geometric Algebra Primer, especially for computer scientists.
Geometric Algebra on PlanetMath
Exploring Hyperspace with the Geometric Product - Highlights applications to higher dimensions and cosmology that includes wormholes.

[0] Cf. Hestenes (1966).

[1] Euclid, Books II and VI.

[2] Hestenes, et al (1984).

[3] Dorst, et al (2007).

[1]

[2]

[3]

[4]