Monte Carlo methods in finance
From Wikipedia, the free encyclopedia
| It has been suggested that Monte Carlo methods for option pricing be merged into this article or section. (Discuss) |
In finance and mathematical finance, Monte Carlo methods are used to value and analyze (complex) instruments, portfolios and investments by simulating the various sources of uncertainty affecting their value, and then determining their average value over the range of resultant outcomes [1]. The advantage of Monte Carlo methods over other techniques increases as the dimensions (sources of uncertainty) of the problem increase.
Monte Carlo methods were first introduced to finance in 1964 by David B. Hertz in "Risk Analysis in Capital Investment" (Harvard Business Review), discussing their application in Corporate Finance. In 1977, Phelim Boyle pioneered the use of simulation in derivative valuation in his seminal paper "Options: A Monte Carlo Approach" (Journal of Financial Economics).
This article discusses typical financial problems in which Monte Carlo methods are used. It also touches on the use of so-called "quasi-random" methods such as the use of Sobol sequences.
Contents |
[edit] Overview
The Monte Carlo Method encompasses any technique of statistical sampling employed to approximate solutions to quantitative problems [2]. Essentially, the Monte Carlo method solves a problem by directly simulating the underlying physical process and then calculating the (average) result of the process [3]. This very general approach is valid in areas such as physics, chemistry, computer science etc.
In finance, the Monte Carlo method is used to simulate the various sources of uncertainty that affect the value of the instrument, portfolio or investment in question, and to then calculate a representative value given these possible values of the underlying inputs [4].
Some examples:
- In Corporate Finance [5], project finance [6] and real options analysis [7], Monte Carlo Methods are used by financial analysts who wish to construct "stochastic" or probabilistic financial models as opposed to the traditional static and deterministic models. Here, in order to analyze the characteristics of a project’s net present value (NPV), the cash flow components that are (heavily [8]) impacted by uncertainty are modeled, mathematically reflecting their "random characteristics". Then, as above, the average NPV of the potential investment - as well as its volatility and other sensitivities - is observed from the resultant histogram of project NPV. This histogram is effectively the project's probability distribution, and, for example, allows for an estimate of the probability that the project has a net present value greater than zero (or any other value) [9]. See further under Corporate finance.
- In valuing an option on equity, the simulation generates several thousand possible (but random) price paths for the underlying share, with the associated exercise value (i.e. "payoff") of the option for each path. These payoffs are then averaged and discounted to today, and this result is the value of the option today [10]; see Monte Carlo option model for discussion as to further - and more complex - option modelling.
- To value bonds, and bond options [11], the underlying source of uncertainty which is simulated is the short rate - the annualized interest rate at which an entity can borrow money for a given period of time. For each possible evolution of interest rates we observe a different yield curve and a different resultant bond price. To determine the bond value, these bond prices are then averaged; to value the bond option, as for equity options, the corresponding exercise values are averaged and present valued. A similar approach is used in valuing swaps and swaptions [12].
- Monte Carlo Methods are used for portfolio evaluation [13]. Here, for each simulation, the (correlated) behaviour of the factors impacting the component instruments is simulated over time, the values of the instruments are calculated, and the portfolio value is then observed. The various portfolio values are then combined in a histogram (i.e. the portfolio's probability distribution), and the statistical characteristics of the portfolio are then observed. A similar approach is used in calculating value at risk [14][15].
- Monte Carlo Methods are used for personal financial planning [16] [17]. For instance, by simulating the overall market, the chances of a 401(k) allowing for retirement on a target income can be calculated. As appropriate, the worker in question can then take greater risks with the retirement portfolio or start saving more money.
Although Monte Carlo methods provide flexibility, and can handle multiple sources of uncertainty, the use of these techniques is nevertheless not always appropriate. In general, simulation methods are preferred to other valuation techniques only when there are several state variables (i.e. several sources of uncertainty) [18]. These techniques are also of limited use in valuing American style derivatives. See below.
[edit] Applicability
[edit] Level of complexity
Many problems in mathematical finance entail the computation of a particular integral (for instance the problem of finding the arbitrage-free value of a particular derivative). In many cases these integrals can be valued analytically, and in still more cases they can be valued using numerical integration, or computed using a partial differential equation (PDE). However when the number of dimensions (or degrees of freedom) in the problem is large, PDEs and numerical integrals become intractable, and in these cases Monte Carlo methods often give better results.
For more than three or four state variables, formulae such as Black Scholes (i.e. analytic solutions) do not exist, while other standard approaches (i.e. numerical methods) such as the Binomial options pricing model and Finite difference methods face several difficulties and are not practical. In these cases, Monte Carlo methods converge to the solution more quickly than numerical methods, require less memory and are easier to program. For simpler situations, however, simulation is not the better solution because it is very time-consuming and computationally intensive.
[edit] American options
Monte-Carlo methods are harder to use with American options. This is because, in contrast to a partial differential equation, the Monte Carlo method really only estimates the option value assuming a given starting point and time.
However, for early exercise, we would also need to know the option value at the intermediate times between the simulation start time and the option expiry time. In the Black-Scholes PDE approach these prices are easily obtained, because the simulation runs backwards from the expiry date. In Monte-Carlo this information is harder to obtain, but it can be done for example using the least squares algorithm of Carriere (see link to original paper) which was made popular a few years later by Longstaff and Schwartz (see link to original paper).
[edit] Monte Carlo methods
[edit] Mathematically
The fundamental theorem of arbitrage-free pricing states that the value of a derivative is equal to the discounted expected value of the derivative payoff where the expectation is taken under the risk-neutral measure [1]. An expectation is, in the language of pure mathematics, simply an integral with respect to the measure. Monte Carlo methods are ideally suited to evaluating difficult integrals (see also Monte Carlo method).
Thus if we suppose that our risk-neutral probability space is  and that we have a derivative H that depends on a set of underlying instruments S1,...,Sn. Then given a sample ω from the probability space the value of the derivative is
and that we have a derivative H that depends on a set of underlying instruments S1,...,Sn. Then given a sample ω from the probability space the value of the derivative is  . Today's value of the derivative is found by taking the expectation over all possible samples and discounting at the risk-free rate. I.e. the derivative has value:
. Today's value of the derivative is found by taking the expectation over all possible samples and discounting at the risk-free rate. I.e. the derivative has value:
where DFT is the discount factor corresponding to the risk-free rate to the final maturity date T years into the future.
Now suppose the integral is hard to compute. We can approximate the integral by generating sample paths and then taking an average. Suppose we generate N samples then
which is much easier to compute.
[edit] Sample paths for standard models
In finance underlying random variables (such as an underlying stock price) are usually assumed to follow a path that is a function of a Brownian motion 2. For example in the standard Black-Scholes model, the stock price evolves as
To sample a path following this distribution from time 0 to T, we chop the time interval into M units of length δt, and approximate the Brownian motion over the interval dt by a single normal variable of mean 0 and variance δt. This leads to a sample path of
for each k between 1 and M. Here each 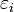 is a draw from a standard normal distribution.
is a draw from a standard normal distribution.
Let us suppose that a derivative H pays the average value of S between 0 and T then a sample path ω corresponds to a set  and
and
We obtain the Monte-Carlo value of this derivative by generating N lots of M normal variables, creating N sample paths and so N values of H, and then taking the average. Commonly the derivative will depend on two or more (possibly correlated) underlyings. The method here can be extended to generate sample paths of several variables, where the normal variables building up the sample paths are appropriately correlated.
It follows from the central limit theorem that quadrupling the number of sample paths approximately halves the error in the simulated price (i.e. the error has order 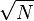 convergence).
convergence).
In practice Monte Carlo methods are used for European-style derivatives involving at least three variables (more direct methods involving numerical integration can usually be used for those problems with only one or two underlyings. See Monte Carlo option model.
[edit] Greeks
Estimates for the "Greeks" of an option i.e. the (mathematical) derivatives of option value with respect to input parameters, can be obtained by numerical differentiation. This can be a time-consuming process (an entire Monte Carlo run must be performed for each "bump" or small change in input parameters). Further, taking numerical derivatives tends to emphasize the error (or noise) in the Monte Carlo value - making it necessary to simulate with a large number of sample paths. Practitioners regard these points as a key problem with using Monte Carlo methods.
[edit] Variance reduction
Square root convergence is slow, and so using the naive approach described above requires using a very large number of sample paths (1 million, say, for a typical problem) in order to obtain an accurate result. This state of affairs can be mitigated by variance reduction techniques. A simple technique is, for every sample path obtained, to take its antithetic path — that is given a path  to also take
to also take  . Not only does this reduce the number of normal samples to be taken to generate N paths, but also reduces the variance of the sample paths, improving the accuracy.
. Not only does this reduce the number of normal samples to be taken to generate N paths, but also reduces the variance of the sample paths, improving the accuracy.
Secondly it is also natural to use a control variate. Let us suppose that we wish to obtain the Monte Carlo value of a derivative H, but know the value analytically of a similar derivative I. Then H* = (Value of H according to Monte Carlo) + (Value of I analytically) − (Value of I according to same Monte Carlo paths) is a better estimate.
[edit] Quasi-random (low-discrepancy) methods
Instead of generating sample paths randomly, it is possible to systematically (and in fact completely deterministically, despite the "quasi-random" in the name) select points in a probability spaces so as to optimally "fill up" the space. The selection of points is a low-discrepancy sequence such as a Sobol sequence. Taking averages of derivative payoffs at points in a low-discrepancy sequence is often more efficient than taking averages of payoffs at random points.
[edit] Notes
- Frequently it is more practical to take expectations under different measures, however these are still fundamentally integrals, and so the same approach can be applied.
- More general processes, such as Levy processes, are also sometimes used. These may also be simulated.
[edit] See also
[edit] References
[edit] Articles
- Boyle, P., Broadie, M. and Glasier, P. Monte Carlo Methods for Security Pricing. Journal of Economic Dynamics and Control, Volume 21, Issues 8-9, Pages 1267-1321
[edit] Books
- Peter E. Kloeden and Eckhard Platen (1992). Numerical Solution of Stochastic Differential Equations. Springer - Verlag.
- Bruno Dupire (1998). Monte Carlo:methodologies and applications for pricing and risk management. Risk.
- John C. Hull (2000). Options, futures and other derivatives (4th ed.). Prentice Hall. ISBN 0-13-015822-4.
- Damiano Brigo, Fabio Mercurio (2001). Interest Rate Models - Theory and Practice with Smile, Inflation and Credit (2nd ed. 2006 ed.). Springer Verlag. ISBN 978-3-540-22149-4.
- Peter Jäckel (2002). Monte Carlo methods in finance. John Wiley and Sons. ISBN 0-471-49741-X.
- Paul Glasserman (2003). Monte Carlo methods in financial engineering. Springer-Verlag. ISBN 0-387-00451-3.
[edit] External links
General
- Free MonteCarlo Simulation Excel Add-in, www.simularsoft.com.ar
- MonteCarlo Simulation in Finance, global-derivatives.com
- Monte Carlo Method, riskglossary.com
- The Monte Carlo Framework, Examples from Finance, Martin Haugh, Columbia University
- Monte Carlo techniques applied to finance, Simon Leger
Derivative valuation
- Monte Carlo Simulation, Prof. Don M. Chance, Louisiana State University
- Option pricing by simulation, Bernt Arne Ødegaard, Norwegian School of Management
- Applications of Monte Carlo Methods in Finance: Option Pricing, Y. Lai and J. Spanier, Claremont Graduate University
- Monte Carlo Derivative valuation, contd., Timothy L. Krehbiel, Oklahoma State University–Stillwater
- Pricing complex options using a simple Monte Carlo Simulation, Peter Fink - reprint at quantnotes.com
- Least-Squares Monte-Carlo for American options by Carriere, 1996, ideas.repec.org
- Least-Squares Monte-Carlo for American options by Longstaff and Schwartz, 2001, repositories.cdlib.org
- Using simulation for option pricing, John Charnes
Corporate Finance
- Real Options with Monte Carlo Simulation, Marco Dias, Pontifícia Universidade Católica do Rio de Janeiro
- Using simulation to calculate the NPV of a project, investmentscience.com
- Simulations, Decision Trees and Scenario Analysis in Valuation Prof. Aswath Damodaran, Stern School of Business
- The Monte Carlo method in Excel Prof. André Farber Solvay Business School
- Sales Forecasting, vertex42.com
- Pricing using Monte Carlo simulation, a practical example, Prof. Giancarlo Vercellino
Value at Risk and portfolio analysis
- Monte Carlo Value-at-Risk, riskglossary.com
Personal finance
- A Better Way to Size Up Your Nest Egg, Businessweek Online: January 22, 2001
- Online Monte Carlo retirement planner with source code, Jim Richmond, 2006
- Free spreadsheet-based retirement calculator and Monte Carlo simulator, by Eric C., 2008
- Financial Planning Using Random Walks, John Norstad, 2005



![S( k\delta t) = S(0) \exp\left( \sum_{i=1}^{k} \left[\left(\mu - \frac{\sigma^2}{2}\right)\delta t + \sigma\varepsilon_i\sqrt{\delta t}\right] \right)](http://upload.wikimedia.org/math/e/c/e/ece42e52fe79512a6490636be13207c8.png)


